PR
データの分析「変量の変換」とは？イメージで掴む変量変換！
データの分析でよく出てくる「変量の変換」。
変量の変換で平均や分散がどのように変化するのか？
変量変換のイメージが掴めれば、公式に頼ることなく平均や分散がどうなるのか？を理解することができます。
この記事では、図を使いながら「変量変換のイメージ」をお伝えしていきます！
目次
「変量の変換」とは？
たろぅ…せんせい。
せんせん？なんですか？
たろぅこのテストのこの問題、出題ミスじゃないですか？ここの分野はテスト範囲じゃないはずですけど…。
せんせふ…そんなバカなことがあるわけないじゃないですか？
どれどれ…。
たろぅここの１０点分の問題ですよ。
せんせ…。
たろぅ間違ってますよね？
せんせいや、間違ってなどいません。
ここは後々テストに出すんだから、要はそれを少し先に出してみただけであって、本当の意味で君たちが勉強をしているのか？を測るテストだと思えば、テスト範囲なんかあるようでないようなもんじゃないですか？そういう意図で考えると、この問題は出題ミスなんかじゃない、ともとれますよね。つまり、私は間違ってなんかいないんです。
たろぅ１０点ください。
せんせ…すいませんでした。
今回のケースは、太郎君だけでなく、テストを受けた生徒全員に＋１０点することになります。
このように、データの分析において、そのデータセットのすべての変量に値を足したり、掛けたりすることを「変量の変換」といいます。
そして、その「変量の変換」が平均や分散などにどのような影響を与えるか？が問題になってきます。
変量の変換
すべての変量\(x\)を\(ax+b\)と変換したとする。
\(x\)の平均を\(\overline x\)、分散を\(s^2\)、標準偏差を\(s\)とすると、\(ax+b\)と変換したとき、
平均：\(a \overline{x} +b\)
分散：\( a^2 s^2\)
標準偏差：\(|a|s\)
となる。
せんせ…今回は、生徒のテストの点数を\(x\)としたときに、すべての\(x\)を\(x+10\)するわけなので、平均は\(\overline{x}+10\)（つまり平均は＋１０点）、分散は変わらない（分散は＋１０の影響を受けない）、ということになりますね。
+bは「底上げ」のイメージ
すべての変数に\(+b\)する、ということは、底上げ（下げ）をするイメージになります。
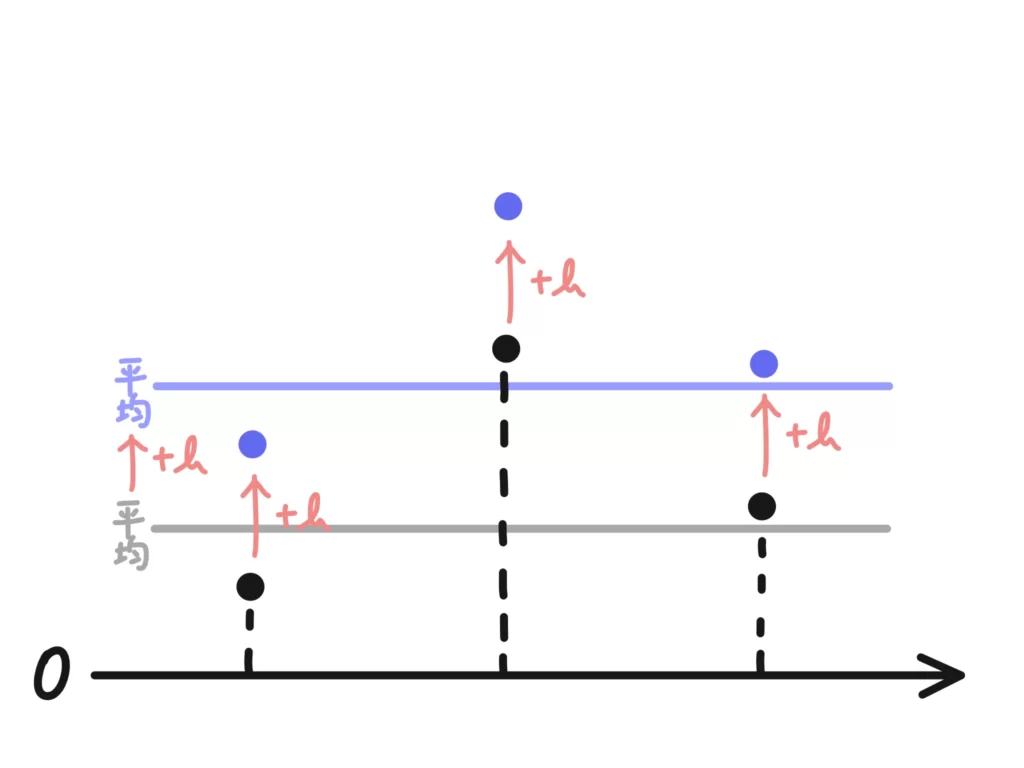
せんせ今回はテストの点を底上げしたイメージになります。
×aは「遠いものは、より遠く」のイメージ
すべての変数に\(\times a\)する、ということは、遠いものをより遠くに配置するイメージになります。
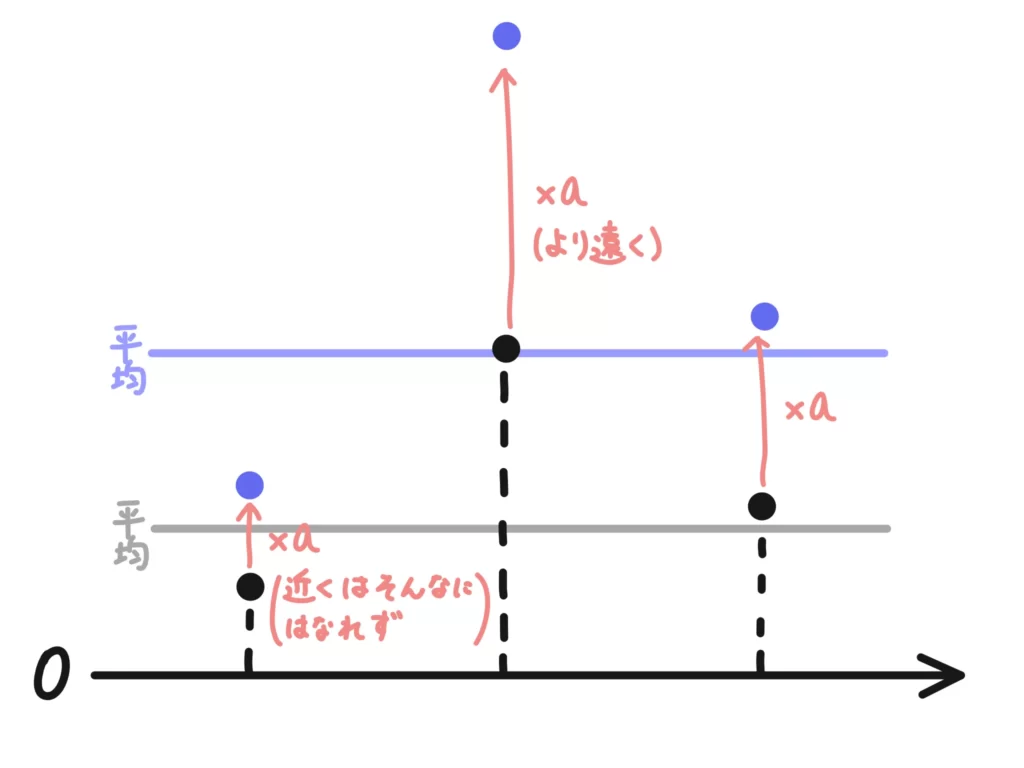
せんせ近いものはそんなに離れず、遠いものはより遠くにデータを配置し直す感じですね。
平均がa×(平均)＋bになる理由
平均は次のように計算することができます。
\(n\)個のデータ、\(x_1\)、\(x_2\)、…、\(x_n\)の平均は
\(\displaystyle \frac{1}{n}(x_1 + x_2 + \cdots + x_n) \)
この計算方法を見てくれればわかりますが、それぞれ \(x_n \rightarrow ax_n+b\)とすれば、平均は\(\times a\)だけ離れた値を取った上で、\(+b\)だけ底上げされます。
平均は、データを単純に足して計算しているからです。（もちろん、その後\(n\)で割りますが、変量変換で影響を受けるデータの部分の話です。）
平均の値に関しては、変量変換の\(\times a\)、\(+b\)の影響をそのまま受けると思っておいてください。
せんせイメージも重要ですが、証明もしておきましょう。
（証）
\(n\)個のデータ、\(x_1\)、\(x_2\)、…、\(x_n\)の平均を
\(\displaystyle \overline{x}= \frac{1}{n}(x_1 + x_2 + \cdots + x_n) \)とする。
すべての変量\(x\)を\(ax+b\)に変量変換すると、平均は、
\(\displaystyle \frac{1}{n} \{ (ax_1+b) + (ax_2+b) + \cdots + (ax_n+b) \} \)
\(\displaystyle \quad = \frac{1}{n} \{ a(x_1+\cdots x_n)+nb \} \)
\(\displaystyle \quad = a \frac{1}{n} (x_1+\cdots x_n)+b \)（← \(\frac{1}{n}\)を展開）
\( \quad = a \overline{x}+b\)（終）
ちなみに、確率統計における変数変換でも同じような考え方ができます。
あわせて読みたい
確率変数の期待値（平均）とは？計算方法や変数変換aX+bでどうなるかを説明
「平均」という言葉は聞いたことがあると思いますが、統計では確率変数のとる値の平均のことを「期待値」とも言われます。 統計での期待値（平均）とはどのような値のこ…
分散がa^2×(分散)になる理由
こちらでも説明していますが、分散は「平均からの散らばり具合」を数値化したものです。
あわせて読みたい
分散はなぜ２乗？求め方や意味をわかりやすく説明
分散は統計で出てくるデータの代表値ですが、その意味はご存じでしょうか？ 「そんなの知ってる！」という人も「何のこっちゃ…」という人もいると思います。では、分散…
各データが平均からばらついていれば値は大きく、平均近くに寄っていれば値は小さくなります。
先ほどの説明で\(+b\)は「底上げ」と言いました。
つまり、\(+b\)は底上げされているだけで平均からのばらつきとは関係ないことがわかります。
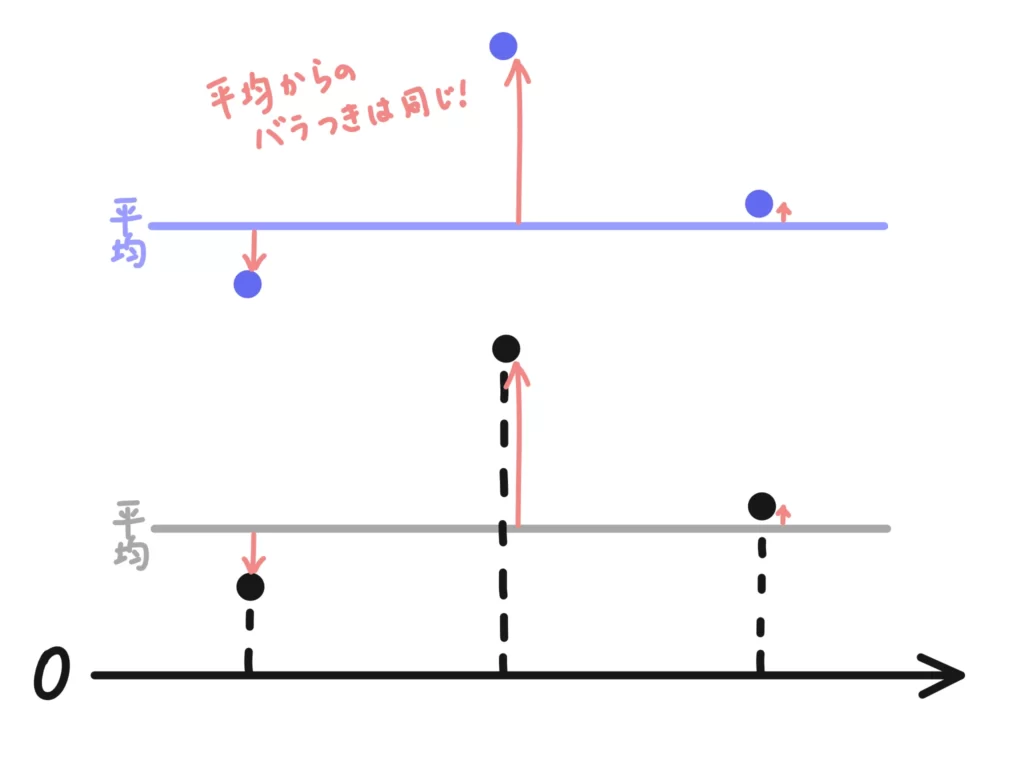
せんせなので、\(+b\)は分散の変量変換に影響しないんですね。
一方、\(\times a \)については、「遠いものはより遠く」というイメージでした。
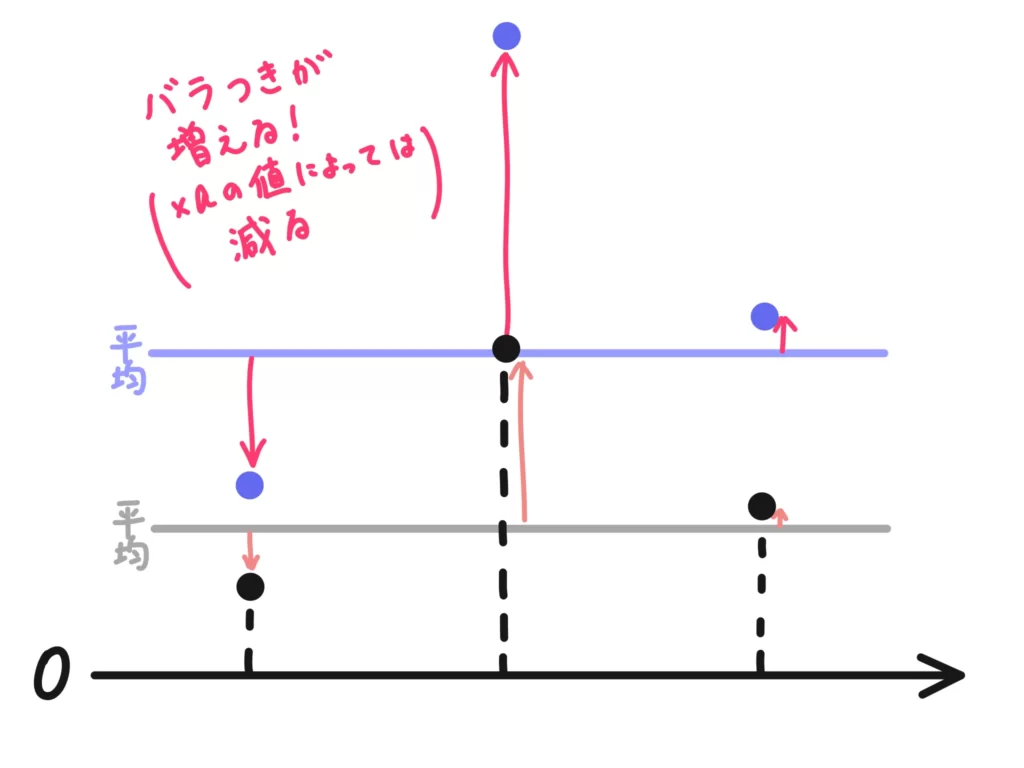
近いものはそこまで離れず、遠いものはより遠くに配置されます。
つまり、平均も\(\times a\)されるのですが、結果的にその平均からのばらつきが増える（減る）のです。
しかも、分散の計算\(\displaystyle s^2 = \frac{1}{n} \{ (x_1-\overline{x})^2+\cdots +(x_n-\overline{x})^2 \} \)を思い出すと、\(x\)は２乗されているので、そこに掛かる\(a\)も２乗されます。
分散が\( a^2 s^2\)となるのはこのような理由です。
せんせこんな感じでイメージしておくと、暗記する必要もないですね。
こちらも念のため、証明しておきましょう。
（証）
\(n\)個のデータ、\(x_1\)、\(x_2\)、…、\(x_n\)の平均を\(\displaystyle \overline{x}\)、
分散を\(\displaystyle s^2 = \frac{1}{n} \{ (x_1-\overline{x})^2+\cdots +(x_n-\overline{x})^2 \} \)とする。
すべての変量\(x\)を\(ax+b\)に変量変換すると、平均は\( a \overline{x}+b\)となる。
分散は、
\(\displaystyle \frac{1}{n} [ \{ax_1+b-(a \overline{x}+b)\}^2 + \cdots + \{ax_n+b-(a \overline{x}+b)\}^2 ] \)
\(\displaystyle \quad = \frac{1}{n}[ \{a(x_1-\overline{x})\}^2+\cdots +\{a(x_n-\overline{x})\}^2] \)（←\(+b\)はこの時点で無くなる）
\(\displaystyle \quad = \frac{1}{n} \{ a^2(x_1-\overline{x})^2+\cdots +a^2(x_n-\overline{x})^2 \} \)
\(\displaystyle \quad =a^2 \frac{1}{n} \{ (x_1-\overline{x})^2+\cdots +(x_n-\overline{x})^2 \} \)
\(\quad = a^2 s^2\)（終）
ちなみに、標準偏差は\(\sqrt{（分散）}\)なので、
\( \sqrt{a^2 s^2} = |a|s\)（←\(s\)は「標準偏差」の意味。変数ではない。）
となります。
こちらも確率統計における変数変換で同じような考え方ができます。
あわせて読みたい
確率統計の分散とは？求め方や変数変換aX+bでどうなるか説明
確率統計の分散はデータの分析で扱った分散と、意味としてはほぼ同じです。 意味合いとしては、データの分析と同じく「平均からどれくらい散らばっているのか？」を示す…
例．なぜ仮平均の計算ができるのか？を変量変換で説明
変量変換の例として、仮平均の考え方があります。
仮平均というのは、そのまま平均を計算するのが大変なときに、一度そのデータの平均になりそうな値を適当に設定してそこからの平均をとる、という方法です。
せんせ言葉ではわかりにくいので、例で説明します。
例．次のデータは５人の身長のデータである。平均を求めよ。
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 身長 | 175cm | 169cm | 180cm | 174cm | 172cm |
このとき、ガチンコで\(\displaystyle \frac{1}{5}(175 + 169 + 180 + 174+ 172)=174\)と計算してもいいんですが、３桁の足し算をしないといけないので面倒です。
ただ、このデータを見たらおよそ平均がどのくらいになるか？は想像ができますよね。
人によっては「平均175cmくらい？」「平均174cmくらい？」「平均176cmくらい？」という感覚は違うかもしれませんが、どんな値でも構いません。
この、「およそ平均がどれくらいになるか？」と予想して設定した値を仮平均といいます。
この仮平均からの差（＋（プラス）、ー（マイナス）の符号付き）を考えて、その平均をとって、仮平均に上乗せすれば元のデータの平均が計算できます。
せんせそれでは、実際に計算してみましょう。仮平均を設定してみてください。
たろぅえ…。大体175cmくらいですかね？
それでは仮平均175cmで計算してみましょう。
（解）
先ほどのデータはこれでした。
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 身長 | 175cm | 169cm | 180cm | 174cm | 172cm |
仮平均を175cmとし、そこからの差をとったデータを表にすると、次のようになります。
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 仮平均175cmからの差 | 0cm | -6cm | +5cm | -1cm | -3cm |
この＋（プラス）、ー（マイナス）付きの値の平均をとります。
\(\displaystyle \frac{1}{5} \{ 0 + (-6) + 5 + (-1) + (-3) \} = -1\)
たろぅ符号は考えないといけないけど、３桁の計算よりは簡単だね。
これを仮平均に上乗せします。
つまり、\( 175+(-1) = 174\)となり、元のデータの平均は174cm…（答）
せんせ確かに先ほどの計算と一致しますね。
ここからが本題です。なぜ仮平均で元の平均が計算できるのか？です。
ただ、先ほどの変量変換したときに平均がどうなるか？を理解した人はなんとなくわかるのではないでしょうか？
要は、変量変換の影響を平均は素直に受ける、というところがポイントです。
「仮平均をとってそこからの差をとる」ということは、その値を水準（＝０）として平均をとるよ、ということになります。これは変量変換の考え方ですよね？
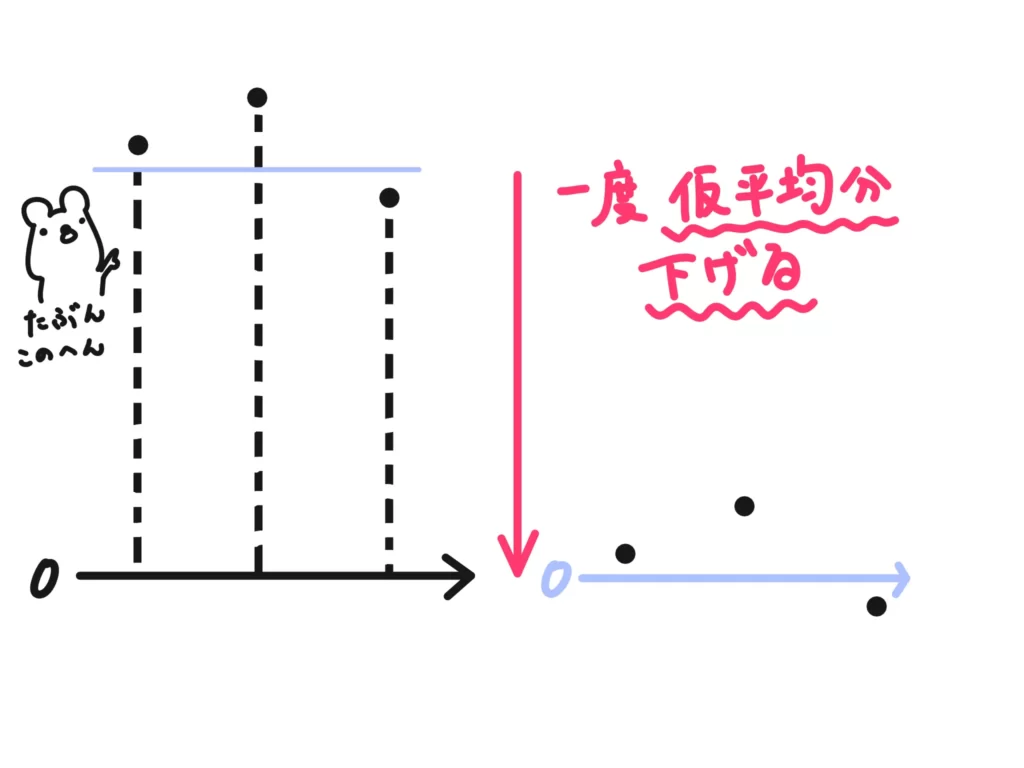
そのあと「その平均を仮平均に上乗せする」という計算で元の平均まで戻す、ということになります。
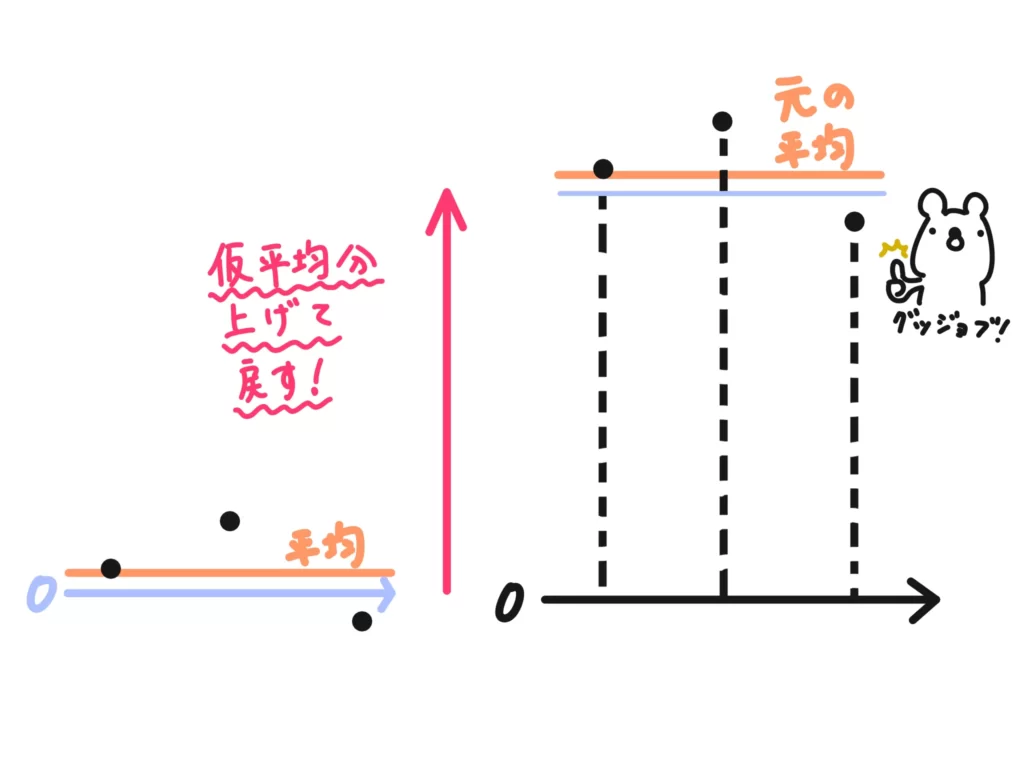
ということで「仮平均の設定」は、変量や平均から値を引いたり、上乗せしたりして、変量変換をしているんですね。
まとめ
「データの分析」は公式を覚えることも必要ですが、どちらかというと「データの扱い方の雰囲気や考え方を掴む」ことが重要になってきます。
最近はSNSの普及もあり、個人や小さな企業でも、データを簡単に大量に収集できるようになってきました。
そこでは、データの値も重要になってきますが、「なぜそのような値になるのだろう？」という原因の分析が欠かせません。
この実際のデータ分析には「想像力」と「論理性」が必要になってきます。
数学は、まさに「想像力」と「論理性」を磨く勉強です。一見データ分析と関係ないようですが、こちらで説明している通り、数学の問題を解くだけで「想像力」や「論理性」が磨かれます。
あわせて読みたい
箱ひげ図のかき方【四分位数や四分位範囲と箱ひげ図の関係もわかる！】
箱ひげ図は中学で習うのですが、これが便利なようで意外と何をしているのかわかりにくいです。 この記事では、箱ひげ図のかき方を説明しながら、箱ひげ図のデータの読み…
あわせて読みたい
不等式の計算で間違えやすい点と変形のポイント
不等式の計算は結構注意して行わないと、間違えることが多い計算です。 なぜ間違える可能性が高いのでしょうか？ この記事では、不等式の計算において注意すべきポイン…
あわせて読みたい
等式・不等式の証明の「正しい書き方」へのコツ
証明…響きがイヤですね。 実際に「証明」と聞いて「うわー…なんか色々書かないといけないやつでしょ？書き方も細かいし、イヤ！嫌い！」という人も（たくさん）いると思…
このあたりが、数学を勉強する最大の理由です。
中・高校生やオトナの人も、数学を勉強するなら、ただ漫然と問題を解くだけでなく、その問題を通して何を学べるか？を意識しましょう。
あわせて読みたい
面白くてオススメの数学本・マンガ
最近よく「オススメの数学の本はありますか？」という質問を受けます。 正直、あんまり本は読まないのですが、これまで読んできた中で「これは面白い！」というオススメ…
ちょっと一息
このブログで活躍してるクマのLINEスタンプもあります！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
