不等式の計算で間違えやすい点と変形のポイント

2022年9月19日2023年12月5日

不等式の計算は結構注意して行わないと、間違えることが多い計算です。

なぜ間違える可能性が高いのでしょうか？

この記事では、不等式の計算において注意すべきポイントをまとめていきたいと思います。

「不等式を解く」って？

そもそも不等式を解く、とはどういうことでしょう？

せんせ

「不等式を解く」って、どういうことですか？

たろぅ

（きたよ…この人はこういう教科書に答えが載ってない質問してくるからキライだ…。）えーっと、急に解くってどういうこと？と言われましても…。どういうことでしょう？

せんせ

じゃあ例えば\( 2x > 6 \)を解けって言われたらどうします？

たろぅ

両辺を２で割って\(x > 3 \)。以上です。

せんせ

そうですね。じゃあ\( 2x > 4y\)は？

たろぅ

同じように両辺を２で割って\( x > 2y \)ですかね。文字があるけど一緒でしょ？

せんせ

４で割って\( \displaystyle y < \frac{x}{2} \)（両辺を入れ替えた）とはしないんですね？

たろぅ

え？なんで急に\(y\)について解いてるんですか？

そもそも「方程式や不等式を解く」と言われたら、「その方程式や不等式を満たす変数の値や範囲を求める」という操作をすることです。

特に２つ目の例のように、文字が複数ある場合はどちらの文字が変数か？を確認する必要があります。

ただ、この先生のように普通はあまり意地悪なことをしません。大体「\(x\)に関する不等式」や「\(a\)を定数とする」といった感じで、どの文字が変数か定数かがわかる書き方をしています。

せんせ

２つ目の例では、\(x\)、\(y\)のどちらが変数か、というのを言ってませんでしたからね。まぁ、特に複数文字があるときは、どれが変数か？（＝それ以外は定数扱い）を意識しといてくださいね、という話です。別に意地悪じゃありません。

条件を確認する、というのは数学でも現実世界でも同じですね。数学力が上がると、こういう現実世界で問題を解くときに「今の問題は何か？それに対する条件はどうなっているか？」を考えるクセがつきます。これが結構効果が大きくて、問題解決の最短距離を導き出すことができます。

鬼門「負の数を掛ける・割る」

せんせ

では、\(-2x > -6\)を解いてください。

たろぅ

ふっふっふ…これはわかりますよ。不等式の場合、両辺に負の数を掛けたり、負の数で割ったりしたら不等号の向きが入れ替わるんでしょ？\(-2\)で割るから、不等号の向きに注意して、\( x < 3 \)だ！

せんせ

なんで不等号の向きを入れ替えるの？

たろぅ

えっ…？答えが合ってる！とかそういうのはないんですか？

せんせ

ま、そこはどうでもいいからね。なんで負の数を掛けたり負の数で割ったら不等号の向きが入れ替わるの？

たろぅ

…なんででしょう。

これは不等式を解く際に一番注意しないといけないところですが、理屈自体はそんなに難しいものではありません。

不等号は「より小さい（or以下）」とか「より大きい（or以上）」という大小関係を表した式だからです。ここに負の数を掛けたり負の数で割ったりするとどうなるか、というのを具体例で見てみればわかりやすいです。

例えば、\(1 < 2\)という不等式は正しいですが、この両辺に\(-1\)を掛けたらどうなるでしょうか？

左辺の1は\(-1\)に、右辺の2は\(-2\)になりますが、そのままの不等号の向きでは\(-1 < -2\)となり、おかしくなりますよね？当然正しい不等式にするには\(-1 > -2\)としなければなりません。

これは、負の数を掛けたり負の数で割ったりした際に、数直線で言うと０を中心に鏡に映したように反対側に移るからです。（もちろん、どんな負の数を掛けるかによって、ただ反対側に移るだけでなく着地地点が伸びたり縮んだりします）

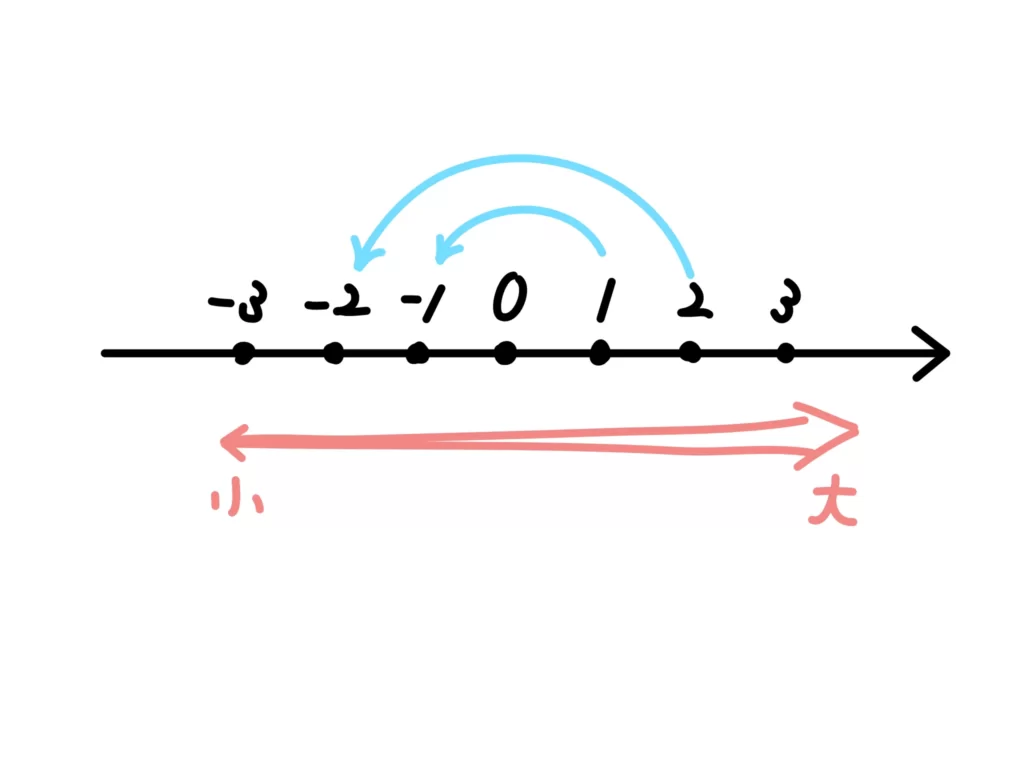
ですので、負の数を掛けたり負の数で割ったりした際に不等号の向きを変える、という操作が必要になってきます。

文字入りの不等式を解いてみよう

せんせ

はい、ではこの記事の最後の問題です。\(x\)についての不等式\(ax > a\)を解いてみてください。

たろぅ

（この記事…？）えーっと、両辺を\(a\)で割って、\(x>1\)です。

せんせ

さっき、なんの話をしたんだ？

たろぅ

負の数を掛けたり負の数で割ったりしたら不等号の向きが変わる、って話ですか？でも\(a\)はマイナスがついてないですよ？

せんせ

見た目上マイナスがついてなければマイナスじゃないの？\(a=-1\)とかいわれたら、\(a\)という文字自体にはマイナスがついてないけど値としてはマイナスなんじゃないの？

たろぅ

…ハイ、スイマセン。ワタシガワルカッタデス、ユルシテクダサイ…。

たろぅ

いや、でも\(a\)がマイナス、とも限らないじゃないですか、\(a=1\)とかいわれたら、\(a\)という文字自体は値としてはプラスなんじゃないですか？

せんせ

そうですね、だから場合分けが必要になってくるんです。

たろぅ

なるほど、\(a\)がプラスかマイナスかで場合分けをするんですね。

場合分け…。これほど高校数学で重要な手法、というか考え方はないでしょう。

場合分けは「解法」と思っている人もいるかもしれませんが、場合分けは解答上必然的にそうしなければならない、どちらかというと記述方法、に近いと思います。まぁ、個人的な意見ですが。

場合分けに隠された重要な考え方、それは「もしもこうだったら…？」という起こりうる全ての可能性を考える、というものです。

人は問題を目の前に置かれると、自分の経験や思い込みを基準に解決しようとしがちです。

が、客観性をもって、常に起こりうる可能性を考えることは重要ですよね？これは、例えば会社の売上向上の戦略を練ったり、学校で文化祭の企画を練ったりする際にかなり重要な姿勢です。「こうかもしれない」という目線が必要になってきます。

そういった考え方の訓練をするのが「場合分け」です。ただ「あぁ、場合分けで解けばいいんでしょ？」という認識では勿体無いです。なぜそこで場合分けが必要なのか？を常に考えましょう。

せんせ

常に「もしこうだったら？」という可能性を考えながら問題を解いていきましょう。今回であれば、パッと計算するのではなく「負の数を掛けたり割ったりするときは不等号が入れ替わる」ことを常に意識しておけば「\(a\)が、もしプラスだったら？もしマイナスだったら？」ということに気づくはずです。

たろぅ

はい。じゃあ答えは「\(a>0\)のときは（不等号の向きが入れ替わらないから）\(x>1\)、\(a<0\)のときは（不等号の向きが入れ替わるから）\(x<1\)」ですね！

せんせ

違います。

たろぅ

もう泣きそう…。

せんせ

そこまで考えたならちゃんと最後まで考えて欲しいですね。「\(a\)がプラスかマイナス」で場合分けしたなら、「じゃあプラスでもマイナスでもない数は？」と思って欲しいところです。

たろぅ

えー…そんな数ないでしょ。

せんせ

ありますよ、ちょうどプラスとマイナスの境目の数です。

たろぅ

あ…。

そうです、「\(a=0\)の場合」を忘れていますね。

せんせ

そもそも「割る」という操作をするんだから、「もしかしたらその文字は０かもしれない」という意識をもっておいて欲しいです。

おまけ

せんせ

先ほどの\(ax > a\)、最終的には同じ答えになりますが、因数分解をする方法もあります。こちらの方が「文字で割る」という危うい操作を含まないので、数学的にはよりスマートです。

せんせ

（＋の値）×？>0のとき、？→（＋の値）、
（ーの値）×？>0のとき、？→（ーの値）となるのがわかればOKです。（（＋）×（＋）>0、（ー）×（ー）>0ですよね？）

\(ax > a\)
\(ax-a > 0\)
\(a \times (x-1) > 0\)
ここで、
\(a > 0\)のとき\(x-1 > 0\)より\(x > 1\)
\(a < 0\)のとき\(x-1 < 0\)より\(x < 1\)
\(a = 0\)のとき不等式は成り立たないので、解なし

まとめ

不等式を解く際にはとにかく「負の数を掛けたり負の数で割ったりするときに不等号の向きが変わる」というのを意識しておいてください。

これは、文字で割ったりする場合も同様です。

常に意識しておいて、状況によっては場合分けになることも頭に入れておきましょう。