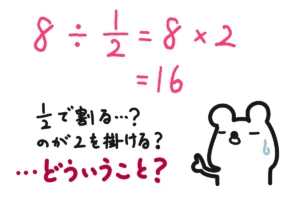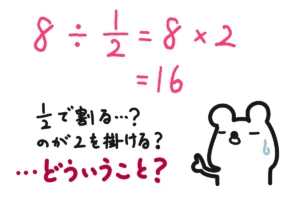PR
0で割れない理由?割ってみればわかる!?

四則演算で、唯一やっちゃいけないこと。それは「0で割る」という計算です。
小学生で習う(ハズ)ですが、まぁ正直あんまり意識することってないんですよね。そもそもそんな問題は中学まであまり無いと思います。
ですが、高校になると状況は一変。文字が大量に出てくる式の式変形をすることになります。このときに、「0で割ってはいけない」ルールが顔を出してきます。
かなり口すっぱく言うんですが、生徒はコレ、なかなか直らないんですよね。具体的には、式変形中に文字で割るときにその文字が0でないことをチェック、もしくは場合分けが必要なんですが、そこの確認をしないんですよ。
では、「なぜ0で割ってはいけないんだろう?」。
この疑問にお答えします。
 せんせ
せんせ今回は数学、というよりも、ちょっとコラム的な感じです。
0で割ったらダメ



せんせい、なんで0で割ったらダメなんですか?



じゃあ割ってみたら?



えっ…。(あいかわらず冷てぇな)
例えば、\( 3 \div 0 \)。答えは?「0」でしょうか?
答えは「そんな計算できない」です。



なんか、別に「答え0」とかでもいい気がするけどなぁ…。
では、少し割られる数を増やしてみましょうか。まずは割る数が0でない、普通の割り算を計算してみましょう。
例えば、\( 1564 \div 23 \)。どうぞ。



ちょっとまって。筆算じゃないと計算できない…。んー…。68?かな、多分。
正解。じゃあ、\( 1564 \div 0 \)。どうぞ。



ん…?



どうかしました?



せんせい、筆算がうまくできません…。ぜんぜん進まないんですけど。



そりゃそうだ。



…。なるほど、0で割ったらダメ、というか0で割る、という計算はできないんですね。
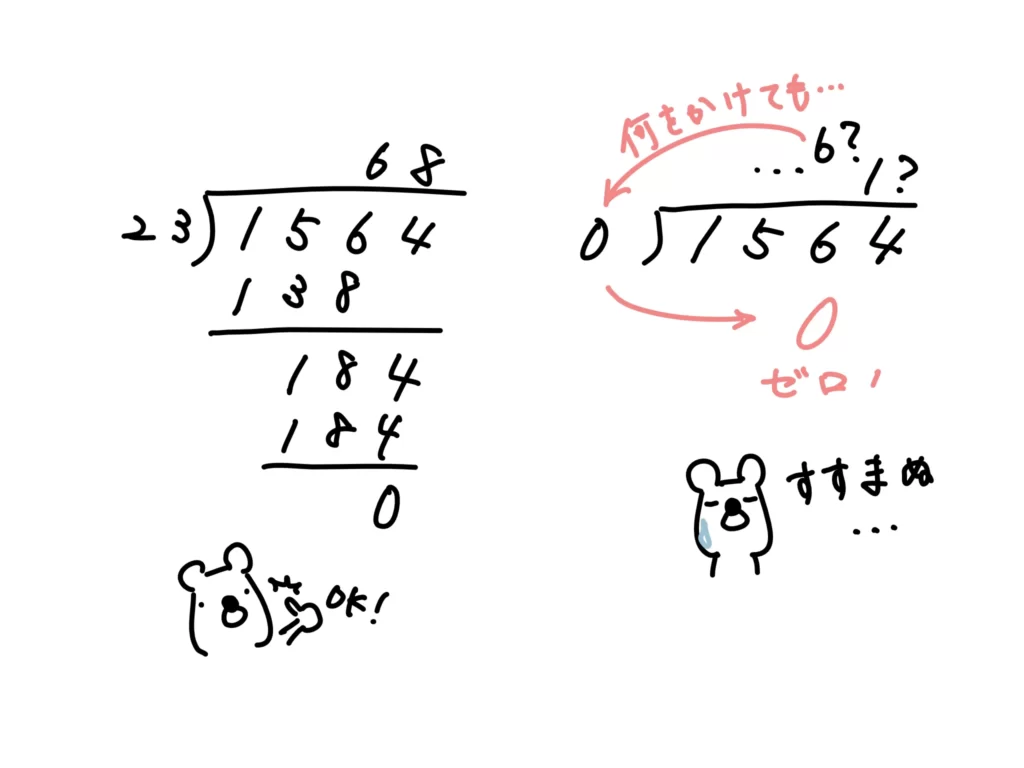
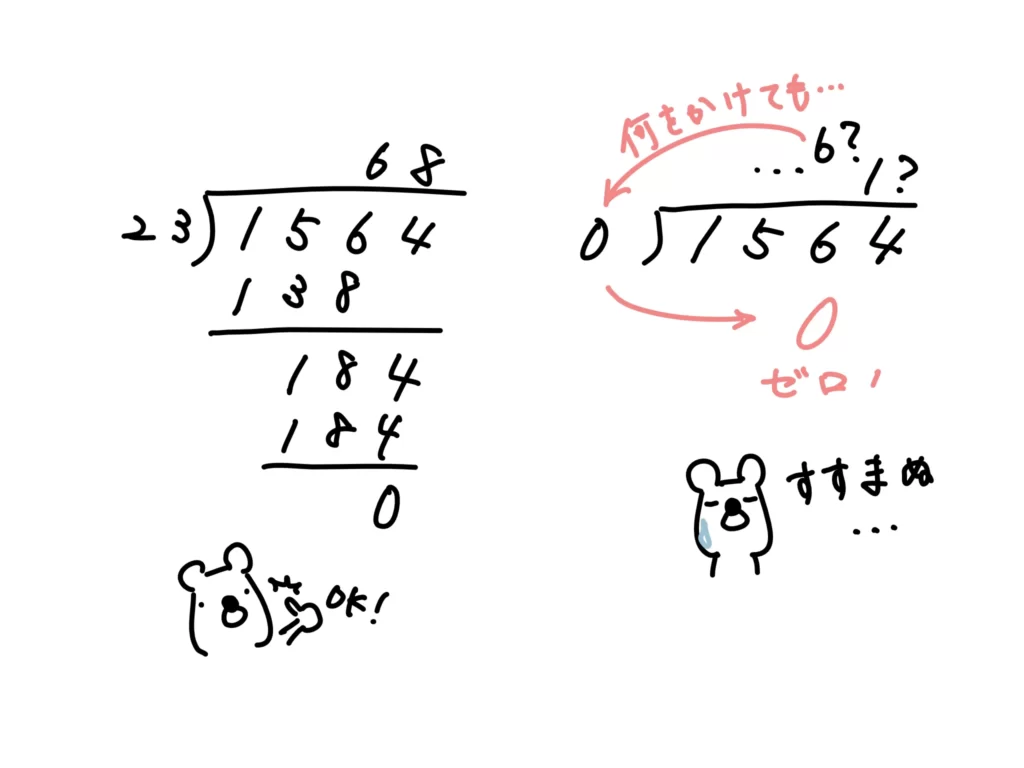
まぁ、ちょっと稚拙な感じがしますが、0で割るという計算が進まない理由がわかりやすいんじゃないでしょうか?
筆算にしてやれば一発ですね。0には何を掛けても0にしかならないので、筆算が進みません。
1=2?
先ほどの例は、実験的にやってみたら0で割るというのは計算できない、という話でしたが、もう少し別の角度からアプローチしてみましょう。
有名な話なのですが、0で割ることを認めてしまうと、おかしな式が導き出されるというものです。



いや、でも0で割る、というのを上手く定義してあげれば0で割る、という操作も可能なんじゃないですか?数学、というのは矛盾なく論理を積み上げることができれば、どんな世界を考えてもいいのでは?非ユークリッド幾何学みたいに平行線が交わる世界だってありうるでしょ?



(なんか急に知ったふうなことを…どうしたんだ、コイツ)でも、0で割ることを認めてしまった時点で、矛盾した式が出てくるんですよ?



…なんでじゃ。
話は変わりますが、数学、というのはとても自由な学問ですね。矛盾なく論理が組み立てられるなら、どんな世界を考えてもいいんだから。
虚数なんかもそうですよね。なんだ、「実在しない数」って。でも、それを定義しちゃうことで、現実世界でもとても役に立つツールになっています。
ただ、その世界が市民権を得るには「論理破綻がない」というのと「役に立つ」ことが必要です。



とりあえず0で割った式に答えを与えちゃうと、ソッコーで矛盾のある式ができちゃいます。だからダメです。



えー…。どんな矛盾が出てくるんですか?
そもそも「割る」ってなに?



そもそも「割る」ってなに?



えーっと…、例えば\( 6 \div 2 = 3 \)っていうのは、6つのモノを2人で分けたら一人3つずつ…みたいな。割る数で分けたら、一人当たりいくつずつに分けられますか?って計算方法だと思います。



25点。



欠点やないか…。
まず、割り算の計算方法には2つのイメージがあります。この2つ、イメージができますか?
1つ目が、たろう君が言った「割る数で等分に分けたら、一人当たりいくつずつにわけられますか?」という考え方です。別に人とは限らないですが、1単位あたりの配分、という意識はもっておいてください。
2つ目が、「割る数のカタマリがいくつできますか?」という考え方です。この例で言えば、「2というカタマリが3つできる」ともとれます。
「割り算」という呼び方なので、1つ目のイメージがパッと思い浮かぶかもしれませんが、実は2つ目のイメージもあります。「分数の割り算」なんかはこっちのイメージの方がわかりやすいですね。
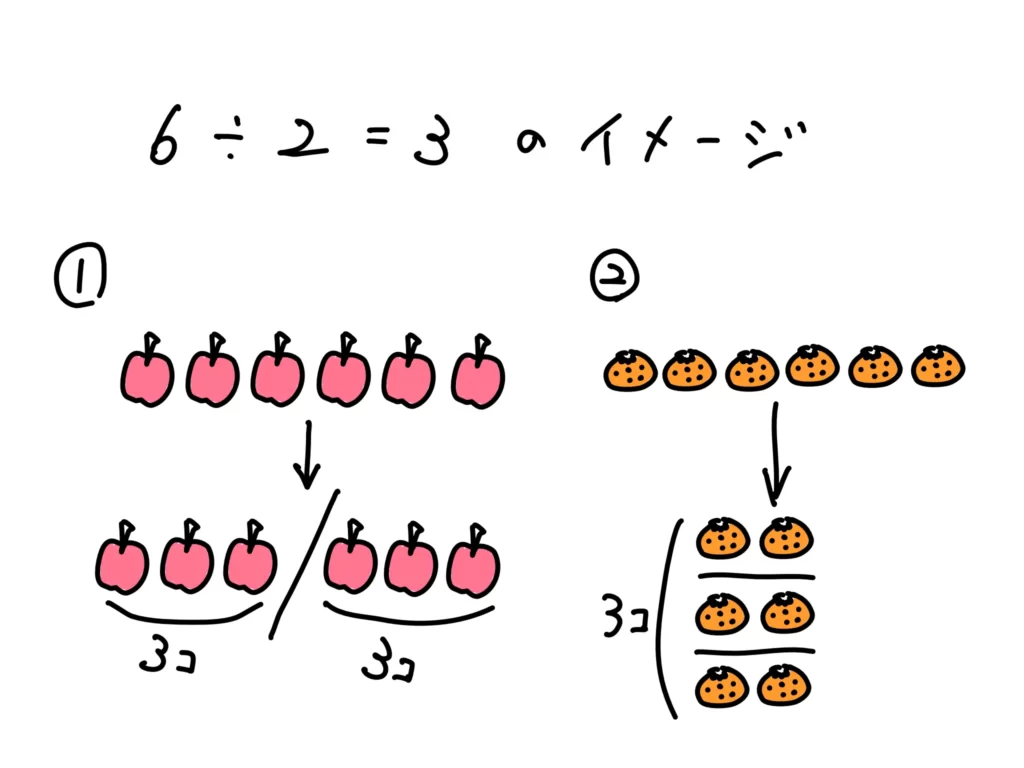
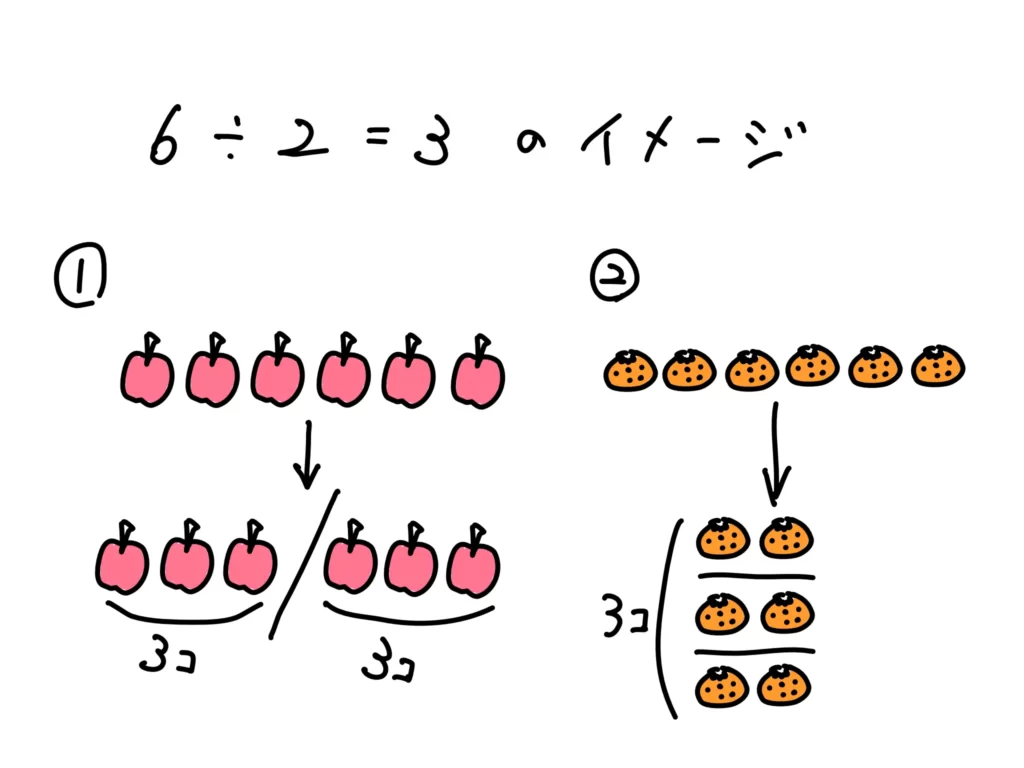



ただ、これは「割り算を計算するときのイメージ」です。正しいんですが、もう少し数学的なアプローチをしていきましょう。
もう少し数学的なアプローチをすると、割り算は掛け算の逆演算で、これをもう一歩進めると、割り算は逆数の掛け算でできる、ということですね。



ん?なんかちょっと急にわかりにくくなったぞ…。
すいません、内容自体は小学生レベルの話です。
割り算は掛け算の逆演算(逆の操作)というのはいいですか?



OKです!足し算に対する引き算、みたいな感じで、掛け算に対する割り算は逆の操作をしてる、ってことですよね?
その通りです。じゃあ、割り算は逆数の掛け算で表現できるってのはいいですか?



…ギリOKです。確か分数をひっくり返して掛けるってやつですよね?
そうですね。例えば、さっきたろう君が\( 6 \div 2 = 3 \)という例を出していました。
割る数2の逆数は\( \displaystyle \frac{1}{2} \)ですよね?つまり、この割り算は、\( \displaystyle 6 \div 2 = 6 \times \frac{1}{2} = 3 \)という風に割り算を逆数の掛け算、とみなすことができます。
ちなみに、「逆数」というのはある数にかけたときに1になる数のことです。(ここからは逆数の説明です。わかるよ、という人は飛ばしてください)



?(わかりにくいぞ)
例えば、「2の逆数は?」と聞かれたとき、先ほどたろう君が言ったように、分数の分母と分子をひっくり返したものが逆数、と言えます。
ex. 2の逆数→\( \displaystyle \frac{2}{1} \)なので、分母と分子をひっくり返すと\( \displaystyle \frac{1}{2} \)となります。
確かに、\( \displaystyle 2 \times \frac{1}{2} = 1 \)なので、この2つの数字はお互いに逆数の関係になります。
では矛盾した式1=2を導いてみましょう
さて、話を戻すと、割り算は逆数の掛け算、とみなすことができます。
ここで、0で割ることができるということを認めると、0の逆数を定義することができる、ということになります。
つまり、\( \displaystyle 0 \times \frac{1}{0} = 1 \)のような数\( \displaystyle \frac{1}{0} \)を認める、ということですね。



さて、じゃあ\( 0=0+0 \)という式を考えてみましょう。この式自体は全く問題ないですよね。



そうですね。



0で割ることを認めてしまうと、さきほど話したように\( \displaystyle \frac{1}{0} \)という数が作れちゃいます。



割り算はその逆数をかけることと同じだからですよね。



そうですね。では、\( 0=0+0 \)の両辺に\( \displaystyle \frac{1}{0} \)を掛けてみましょう。
\( \displaystyle 0 \times \frac{1}{0}=(0+0) \times \frac{1}{0} \)
\( \displaystyle 0 \times \frac{1}{0}=0 \times \frac{1}{0} + 0 \times \frac{1}{0} \) (展開)
\( 1=1 + 1 \)
\( 1=2 \)



…。おかしいですね。



それみたことか。



むぅ…。なぜこんなことが起きるんだ…。



じゃあ、それを考えてみようか。



さらに攻めてくるか…。厳しいな…。
さて、ここらへんまで解説しているサイトは結構あるのですが、せっかくなのでなぜこんなことになるのか考えてみましょう。
なぜこんな矛盾した式が出てくるかわかりますか?



ヒントは「0に何かの数を掛けたときにどうなるか」ですね。



0にはどんな数を掛けても0になるでしょう。\( 0 \times 1 = 0\)、\( 0 \times (-1) = 0 \)、\( 0 \times \displaystyle \frac{1}{2} = 0 \)、\( 0 \times \sqrt{2} = 0 \)、何を掛けても0になりますよ、そりゃ。当たり前です。



…0にはどんな数を掛けても0になりますよね?ですよね?



あ…。
ということで、わかりましたかね?
\( \displaystyle \frac{1}{0} \)という数は、\( \displaystyle 0 \times \frac{1}{0} = 1 \)を満たすので、0に掛けても0にならない数と言えます。
矛盾した式が出てくる理由。それは、0という何もない数に\( \displaystyle \frac{1}{0} \)という数をかけることで1という数が生み出されるからです。



手品の鳩のようなもんですね。
まとめ
0で割ってはいけない…まぁ、正直言って高校生か大学で数学を勉強している人以外は忘れているんじゃないかな、と思います。なぜなら、0で割るなんてことを普通はしないからです。
ただ、コラム的に知っておいて面白い話ですし、高校生は冒頭で言ったように、式変形をするときに必ず注意しないといけない部分になります。
ということで、「0で割ってはいけないんだ」ということは頭の片隅に置いておきましょう。