PR
グラフの平行移動はこれを押さえれば完璧!【二次関数の例で理解する】

さて皆さん、いきなりですが問題です。
関数\(y=(x-1)^2+1\)が表すグラフの頂点の座標を求めよ。
…答えは(1,1)ですね。
簡単に説明すると、
\(y=(x-1)^2+1\)の\( x-1\)を見て、頂点の\(x\)座標を\(1\)、
\(y=(x-1)^2+1\)の最後の\(+1\)を見て、頂点の\(y\)座標を\(1\)
と読みます。
しかし、ここで疑問に思うのは、
「なんで\(x-1\)を見て『頂点の\(x\)座標を\(1\)』と判断して、\(+1\)を見て『頂点の\(y\)座標を\(1\)』と判断するの?」
というところではないでしょうか。マイナスがついたり、つかなかったり…わかりにくいですよね?
 デカ丸
デカ丸なんで\(x-1\)を見て「頂点の\(x\)座標\(1\)」って読むんじゃい!
実はここが理解できると、この後「グラフ(や図)の平行移動」が全て同じように理解できます。
ということで、この記事ではグラフ(や図)の平行移動について話をしていきます。
グラフや図の平行移動をどう説明するか



…



どうかしましたか?



せんせい…なんで\(y=(x-1)^2+1\)のグラフの頂点の座標が(1,1)なんですか?\(x-1\)だから…\(x\)座標が1?最後の\(+1\)で\(y\)座標が1?…帰っていいですか?



確かに2次関数の頂点の座標は読みにくいですよね。実は数学IIの「軌跡」の話を知っていると理解がしやすいのですが、ついでだから説明しちゃいますか。



数学II…しまった



ヤブヘビだった、って顔してんな
実はこれ、数学IIの「軌跡」の話なんですが…そこは少し置いておいて、二次関数のお話をしましょう。
2次関数のグラフの平行移動をおさらい
二次関数の平行移動(頂点が原点以外のところに移動する)については、大体次のような流れで説明していきます。
例1.\(y=x^2+1\)の頂点は?
①大体こんな表をかかせる。
| x | … | -2 | -1 | 0 | 1 | 2 | … |
|---|---|---|---|---|---|---|---|
| y | … | 5 | 2 | 1 | 2 | 5 | … |
②表を元にこんなグラフをかかせる。
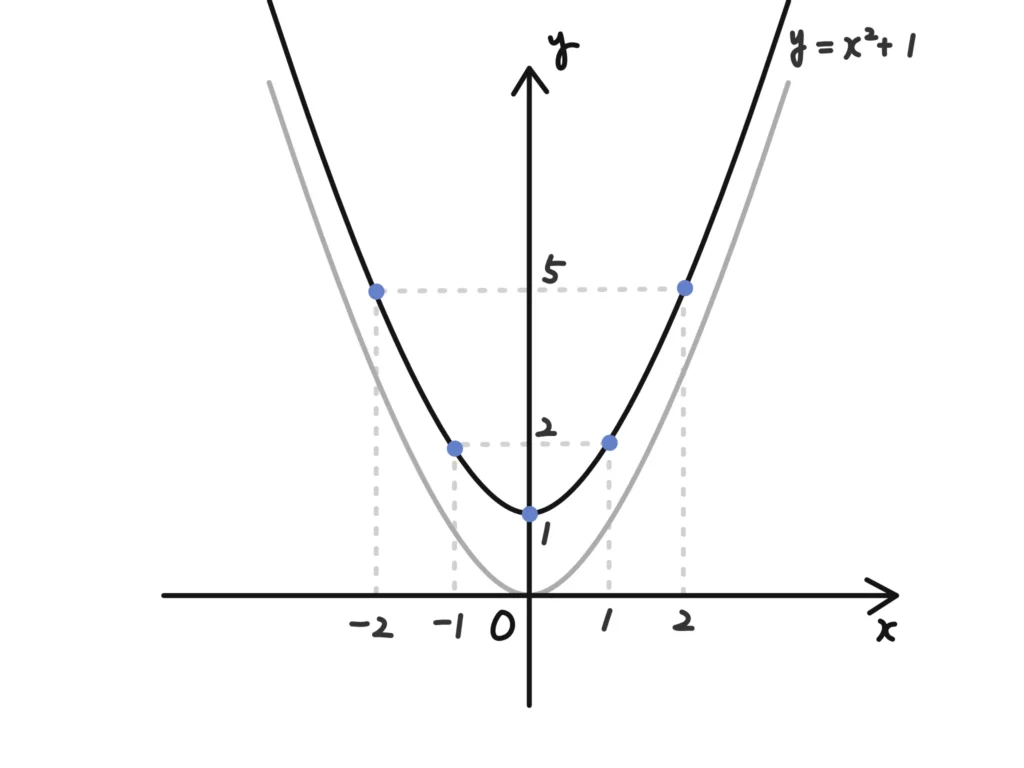

一般化して、
二次関数\(y=ap^2+q\)が表すグラフの頂点の座標は\( (0 , q)\)



まぁ\(+q\)を見て縦方向に\(q\)動くってのはまぁわかるかも。
例2.\(y=(x-1)^2\)の頂点は?
①大体こんな表をかかせる。
| x | … | -2 | -1 | 0 | 1 | 2 | … |
|---|---|---|---|---|---|---|---|
| y | … | 9 | 4 | 1 | 0 | 1 | … |
②表を元にこんなグラフをかかせる。
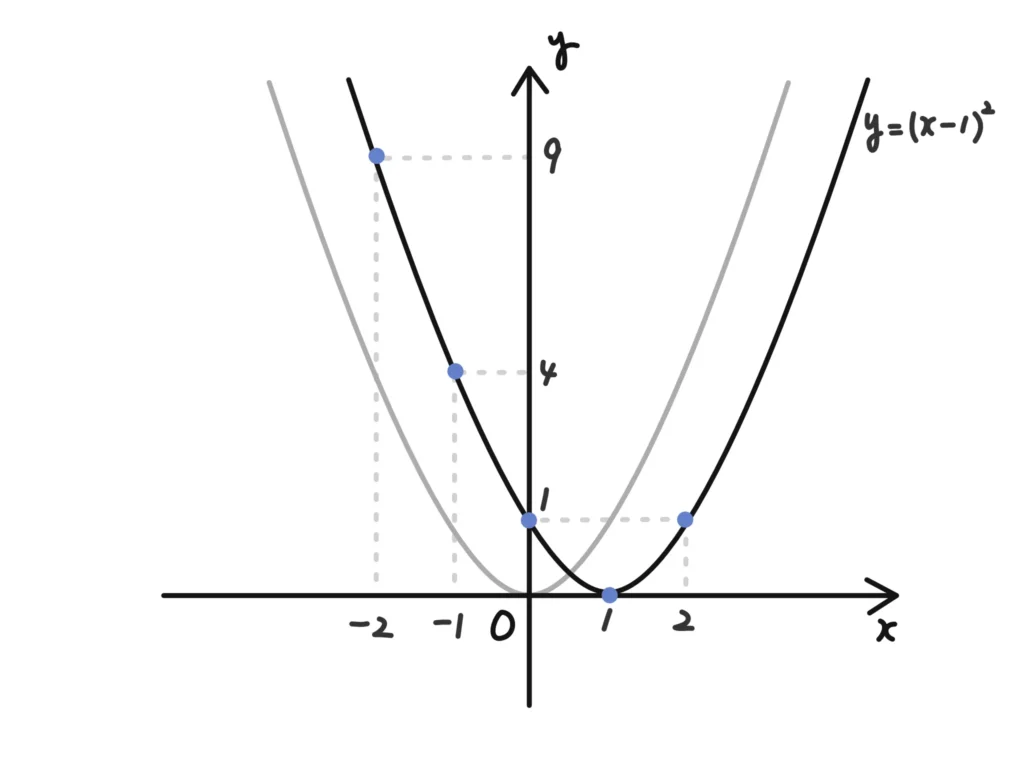

一般化して、
二次関数\(y=a(x-p)^2\)が表すグラフの頂点の座標は\( (p , 0)\)



…なんかこのあたりから騙されてる感が
大体納得いかなくなったくらいに、トドメの
例3.\(y=(x-1)^2+1\)の頂点は?
①大体こんな表をかかせる。
| x | … | -2 | -1 | 0 | 1 | 2 | … |
|---|---|---|---|---|---|---|---|
| y | … | 10 | 5 | 2 | 1 | 2 | … |
②表を元にこんなグラフをかかせる。
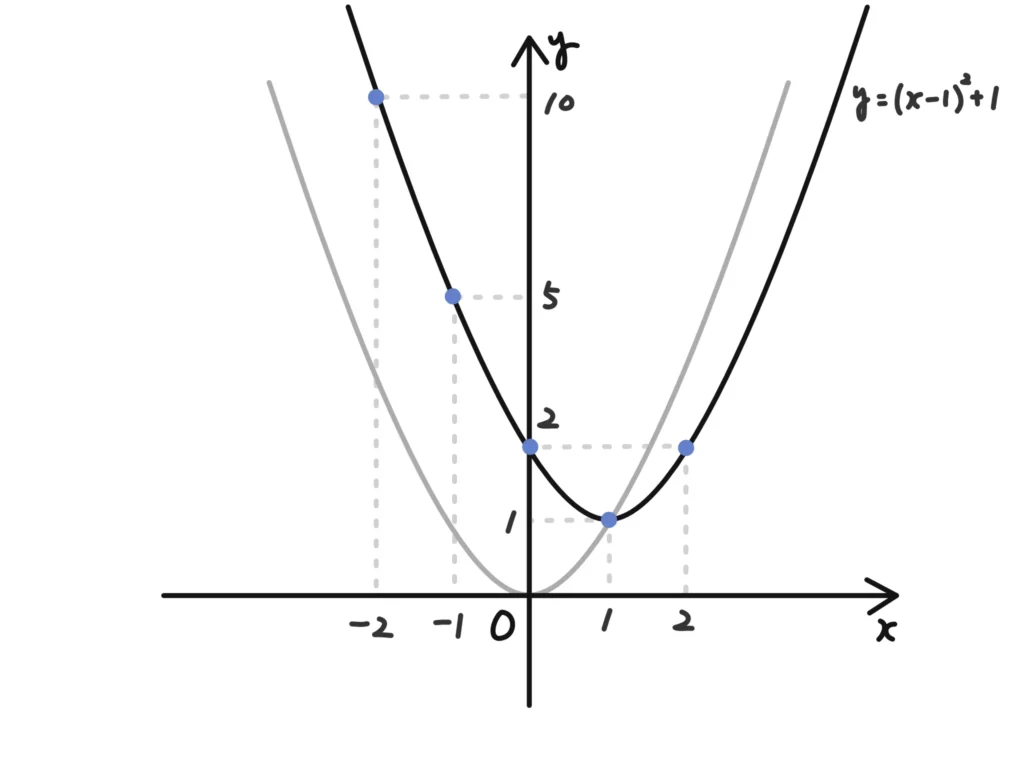

で、
二次関数\(y=a(x-p)^2+q\)が表すグラフの頂点の座標は\( (p , q)\)
と、一般化されます。まぁこれで「そんなもんか」と思ってくれればいいのですが…。



でもやっぱり違和感があるというか、騙された感があるというか…。
2次関数のグラフを平行移動する際のちょっと突っ込んだ考え方
ということで、少し一般的な考え方を説明します。
y軸(縦)方向の平行移動
例1’.\(y=x^2+q\)の頂点は?
ポイントは\(y=…\)の最後に\(+q\)されている、というところです。つまり、
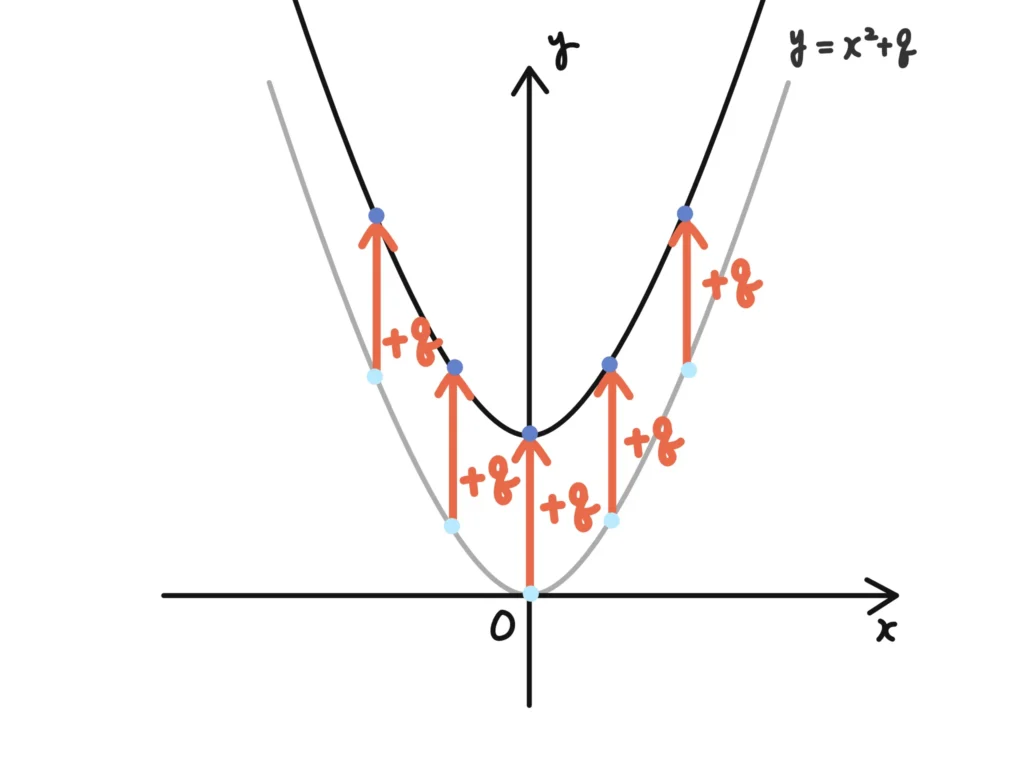

こんな感じになります。
要は、すべての\(x\)に関して、\(x^2\)を計算した上で\(+q\)するので、
\(y\)軸(縦)方向に\(+q\)平行移動する
ということになります。



なるほど、\(+q\)で底上げ(下げ)されるイメージなのか…。
x軸(横)方向の平行移動
例2’.\(y=(x-p)^2\)の頂点は?
ここらへんがちょっとわかりにくいのですが、先に\(x\)の部分を\(x-p\)にしています。つまり、
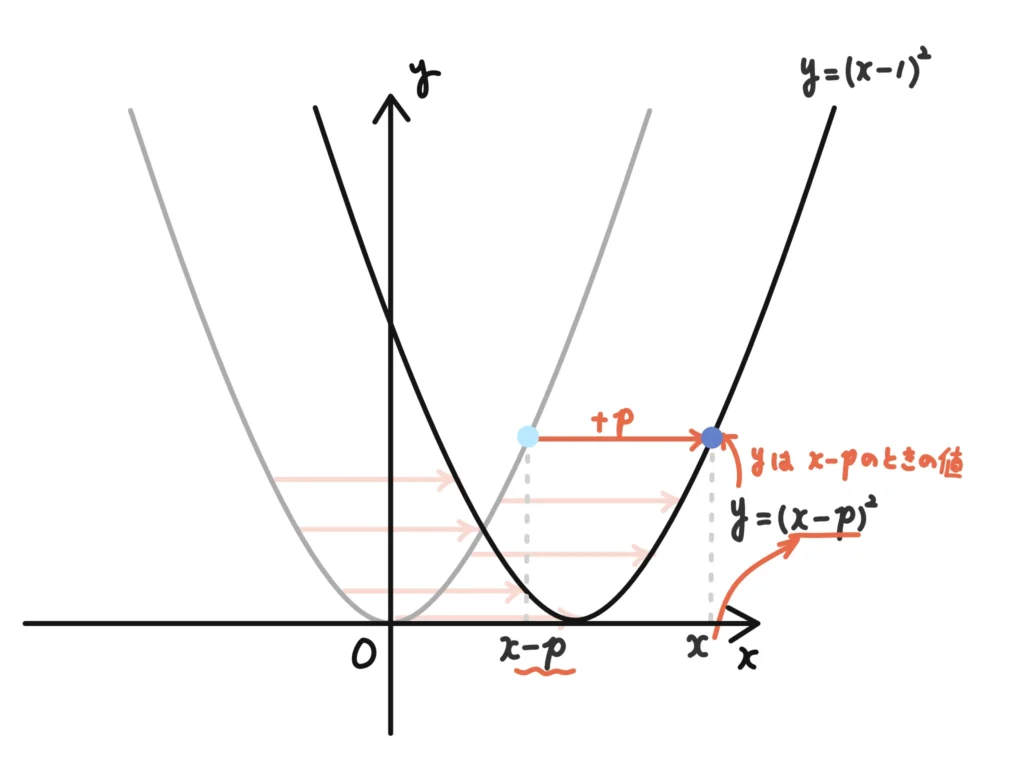

こんな感じになります。
要は、すべての\(x\)に関して、\(x-p\)を計算した段階で
\(x-p\)の位置の\(y\)の値を\(x\)にまでズラす感じ=\(x\)軸(縦)方向に\(+p\)だけ平行移動する
ということになります。



なるほど…元のグラフの\(x-p\)の位置にある点を\(x\)のところにもってくるから、\(+p\)だけ横にずれる…という感じかな?
注意点としては、先に\(x\)を\(x-p\)として計算しないといけないので、
\(y=x^2\)を平行移動させたいなら
\(x\)を\(x-p\) → 2乗 → \(y=(x-p)^2\)
となります。
合わせ技で平行移動
ここまでわかれば、あとはそんなに難しくないです。
例3’.\(y=(x-p)^2+q\)の頂点は?
- \(x\)を\(x-p\)とする → \(x\)軸(縦)方向に\(+p\)だけ平行移動
- \((x-p)^2\)を計算したあと\(+q\)する → \(y\)軸(縦)方向に\(+q\)平行移動する
なので、合わせ技で頂点が\( (p, q) \)に移動することになります。
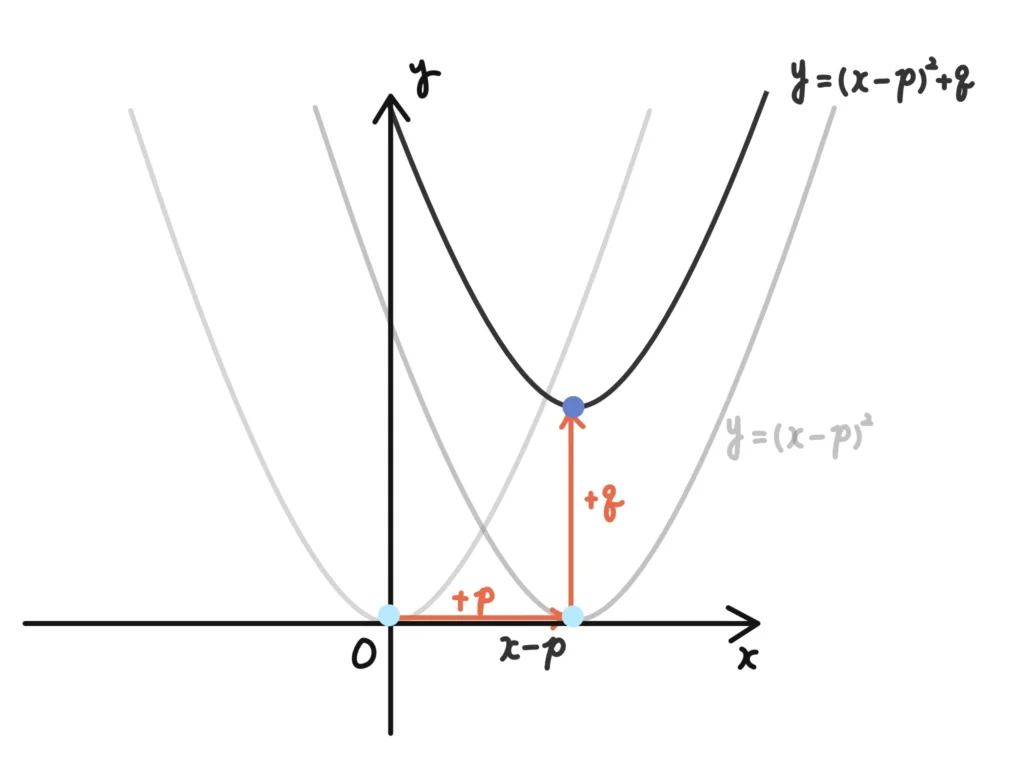




なるほど!わかったぞ!もう大丈夫です!



それじゃ軌跡の話をしますか。



もういいのに…



でもまぁ、軌跡の話を知っておくとすべてのグラフ(図)の平行移動の話が理解できるからオススメですよ。
グラフの平行移動を軌跡で理解する
とりあえずここまでで2次関数の平行移動が理解できればOKですが、後々のためにも軌跡の話を知っておくのをオススメします。



数学IIの話なので、まだ習ってないよ〜という人は無理しなくてもいいですが。
軌跡とは
軌跡は、「ある条件を満たしながら動く点」の「動く跡の方程式を求める」という話です。
やり方としては…
- 求める軌跡の動点の座標を\((x,y)\)とおく。
- その\(x\)、\(y\)の関係式を条件から求める。
という流れです。



本当は軌跡を求める際の注意点があるのですが、この記事のメインは「平行移動」なので、早速そっちの話を進めます。
ということで、平行移動したグラフを表す関数の軌跡を求めてみましょう。



まず、移動する前のグラフの関数を\(y=f(x)\)としましょう。
ゴールは、
\(y=f(x)\)を\(x\)軸方向に\(p\)、\(y\)軸方向に\(b\)だけ平行移動したグラフの軌跡を求める
ことです。
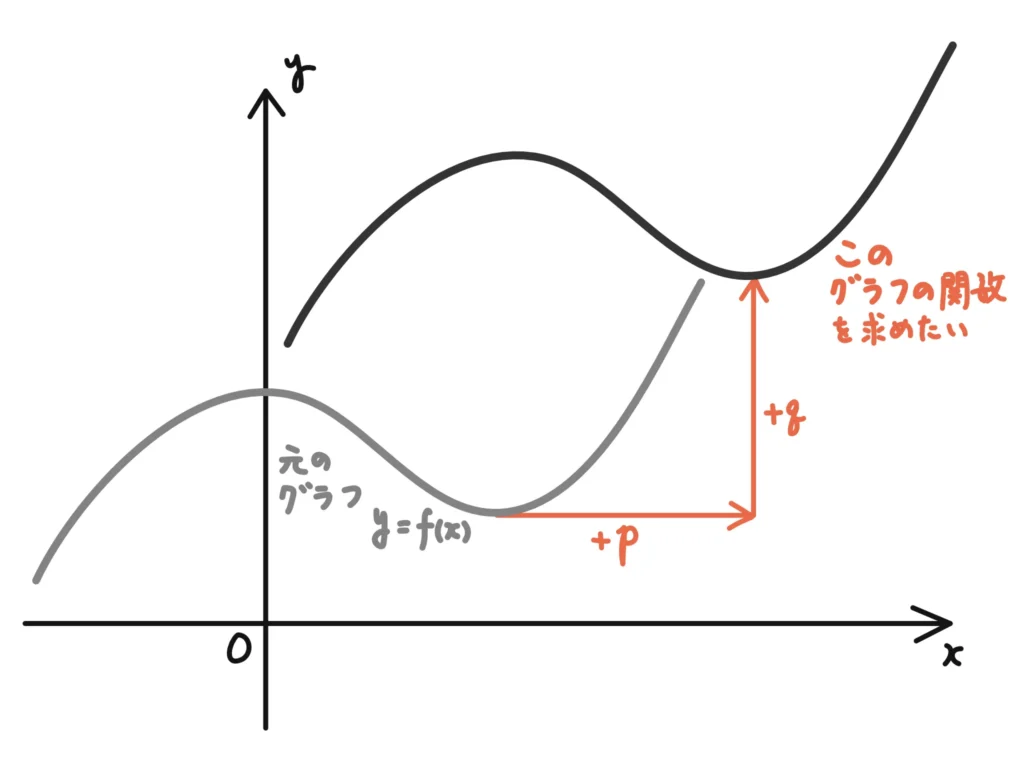

つまり、「元のグラフから\(x\)軸方向に\(p\)、\(y\)軸方向に\(b\)だけ平行移動した点」の「動く跡の方程式を求める」
というお話です。



\(y=f(x)\)とか出てきてちょっと抽象的な話になりますが、注釈を入れながら進めていきます。
ですが、このような抽象的な式を使った議論も数学では重要です。少しずつ慣れていきましょう。
① まず、求める軌跡(平行移動したグラフ)の点を\( P(X, Y) \)とします。
この\(X\)と\(Y\)の関係式を作れば、軌跡を求めたことになります。
これがこの問題のゴールです。覚えておきましょう。



点を\( (x,y) \)と置くのがセオリーですが、\(y=f(x)\)の\(x\)、\(y\)とごっちゃになるので「\(X\)と\(Y\)の関係式を求める」としておきます。
② 元のグラフを表す関数を\(y=f(x)\)として、Pの元(平行移動する前)を表す点を\(Q(a,b)\)とします。
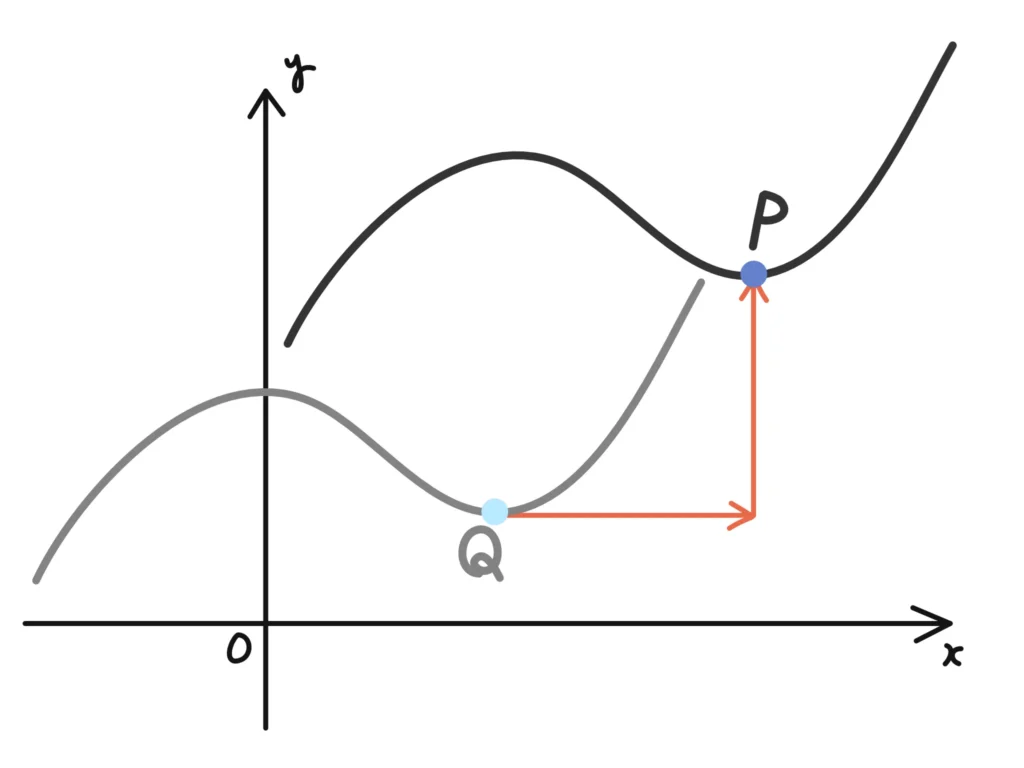

③ すると、\(Q(a,b)\)と\( P(X, Y) \)の間には、
\(X=a+p , Y=b+q\)
という関係式が成り立ちます。
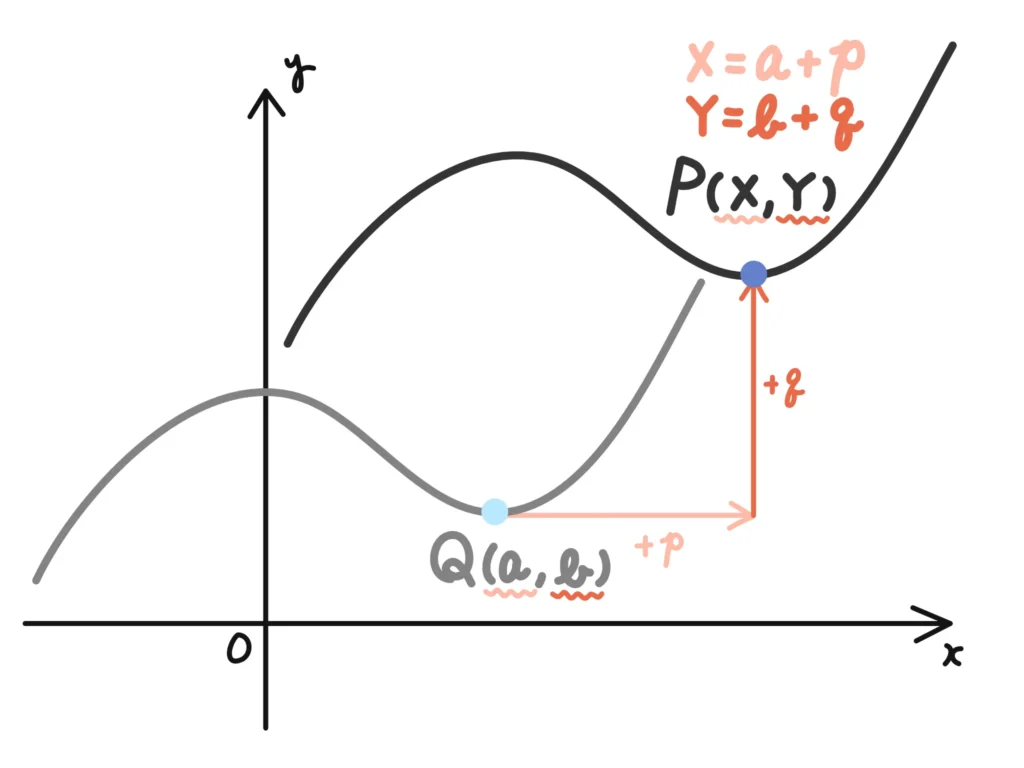

④ 一方、ゴールである\(X\)、\(Y\)の関係式は直接わかりませんが、関係式がある文字がこの中に存在します。
それは\(Q(a,b)\)の座標である\(a\)と\(b\)です。
\(Q\)は\(y=f(x)\)上にあるので、\(b=f(a)\)という関係式…※が成り立ちます。



ま、点がグラフ上にあれば、その座標を代入してもOKだからね。
⑤ ③で\(X=a+p , Y=b+q\)が成り立つことは確認しました。
ここから、式を変形して\(a = X-p , b = Y-q\)とします。



なんでわざわざこんな形に変形するんだ?
この\(a = X-p , b = Y-q\)を\(b=f(a)\)という関係式(※の式)に代入します。
すると、
\(Y-q=f(X-a)\)
という関係式が得られます。



ん?で?
…もう一度ゴールを思い出しましょう。ゴールは\(X\)と\(Y\)の関係式を作ることです。
この\(Y-q=f(X-a)\)は、まさに\(X\)と\(Y\)の関係式ですよね。



なるほど…なんかいつの間にか平行移動した点の座標の関係式が出てたのか…。
\(X\)、\(Y\)は軌跡を求めるためにわかりやすく設定した文字なので、実際には\(x\)、\(y\)としてOKです。
つまり、\(y=f(x)\)を平行移動したグラフの軌跡は\(y-q=f(x-a)\)として表すことができます。
\(y=f(x)\)を
\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動したグラフ(図)の方程式は
\(y-q=f(x-p)\)
と表すことができる。
言い換えると、
\(x \rightarrow x-p\)、\(y \rightarrow y-q \)と置き換えれば、平行移動したグラフを求めることができる。
この考え方はかなり使えます。必ず押さえておいてください。
もう一度2次関数のグラフの平行移動を考えてみよう



よし、じゃあもう一回2次関数のグラフに戻るよ〜。



もうお腹いっぱいザンス…
例3’.\(y=(x-p)^2+q\)の頂点は?
の結果を、軌跡を使った平行移動から説明してみましょう。



…無視ですか
\(y=(x-p)^2+q\)の頂点は\( (p, q) \)になる、というのは確認しました。
これを軌跡の平行移動、という目線で考えると、
\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動したグラフなので、
元の\(y=x^2\)を\(x \rightarrow x-p\)、\(y \rightarrow y-q \)と置き換えればよい、
ということになります。つまり、
\(y-q=(x-p)^2\)
とすれば、頂点\( (p, q) \)になります。



あら?なんか形が違うぞ?
関数は\(y=…\)の形にしておくのが基本なので、\(y-q=(x-p)^2\)の\(-q\)を移項します。すると、
\(y=(x-p)^2+q\)
となりますよね?



はぁ…この\(+q\)って、元々\(y\)を\(y-q\)に置き換えたときに\(y=…\)の形にする際に出てきたのか。
…という風に解釈することもできます!
つまり、平行移動の考え方だと、\(x-p\)よりも、むしろ\(+q\)の方がイレギュラーなんですね!



この\(x \rightarrow x-p\)、\(y \rightarrow y-q \)と置き換える考え方はすべてのグラフ(図)に使えます!
すごいぞ!置き換えによるグラフの平行移動!



それでは、「置き換えによる平行移動」の威力を見ていただきましょう!
直線の方程式(数学II)
点\( (p,q) \)を通る、傾き\(m\)の直線の方程式は
\( y-q = m(x-p) \)
これなんかはそのままですね。
原点を通る、傾き\(m\)の直線は\(y=mx\)です。
このとき、平行移動の点としてわかりやすいのは原点\((0,0)\)ですね。\((0,0)\)が\((p,q)\)に平行移動した、と考えます。
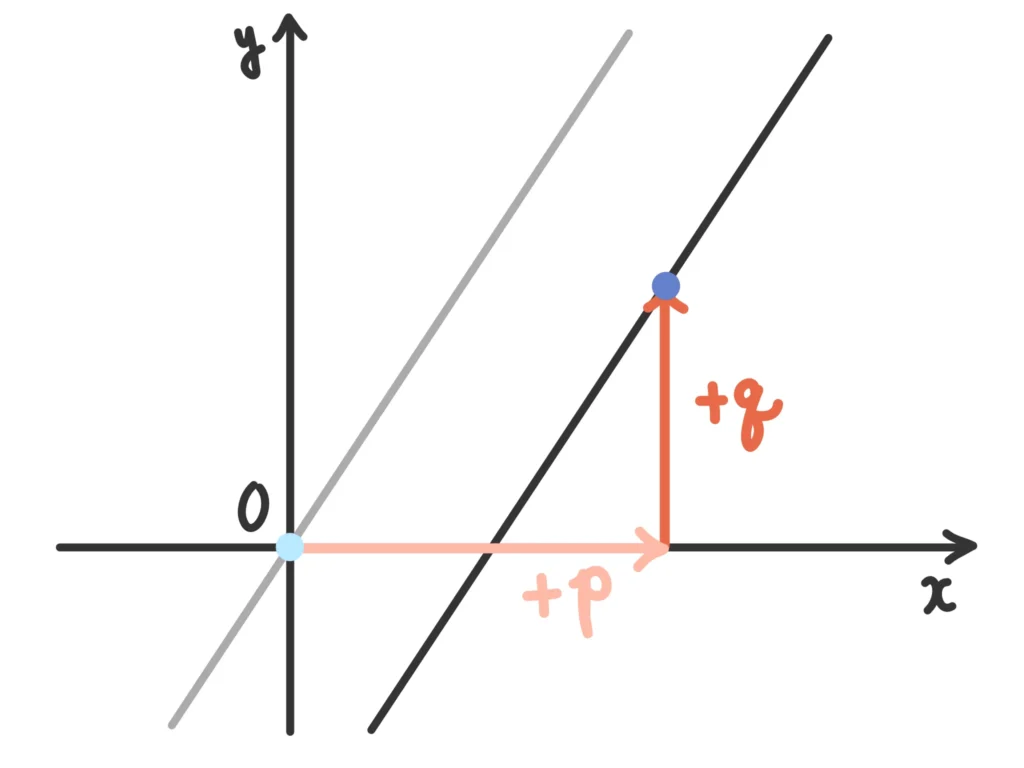

つまり、\(x \rightarrow x-p\)、\(y \rightarrow y-q \)と置き換えると先ほどの、
\( y-q = m(x-p) \)が得られます。



なるほど。
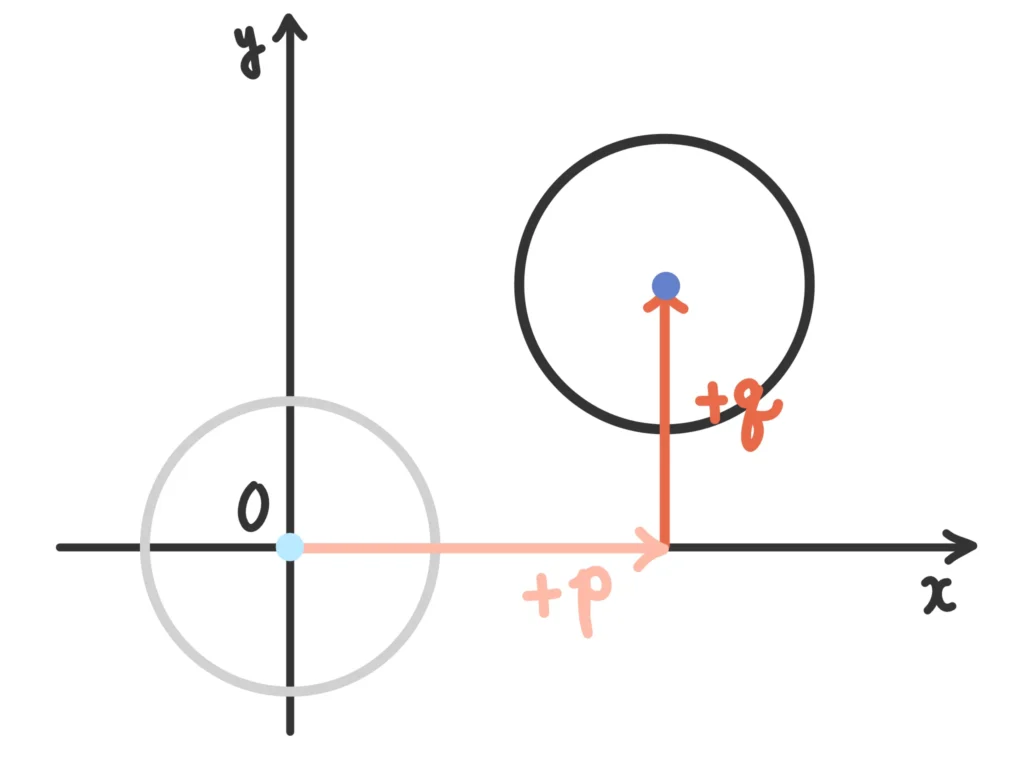
円の方程式(数学II)
原点中心、半径\(r\)の円の方程式は次のようになります。
\( x^2+y^2=r^2\)
中心が\((p,q)\)、半径\(r\)の円の方程式は次のようになります。
\((x-p)^2+(y-q)^2=r^2\)
これも平行移動ですね。\(x \rightarrow x-p\)、\(y \rightarrow y-q \)と置き換えていますね。



なるほど…。

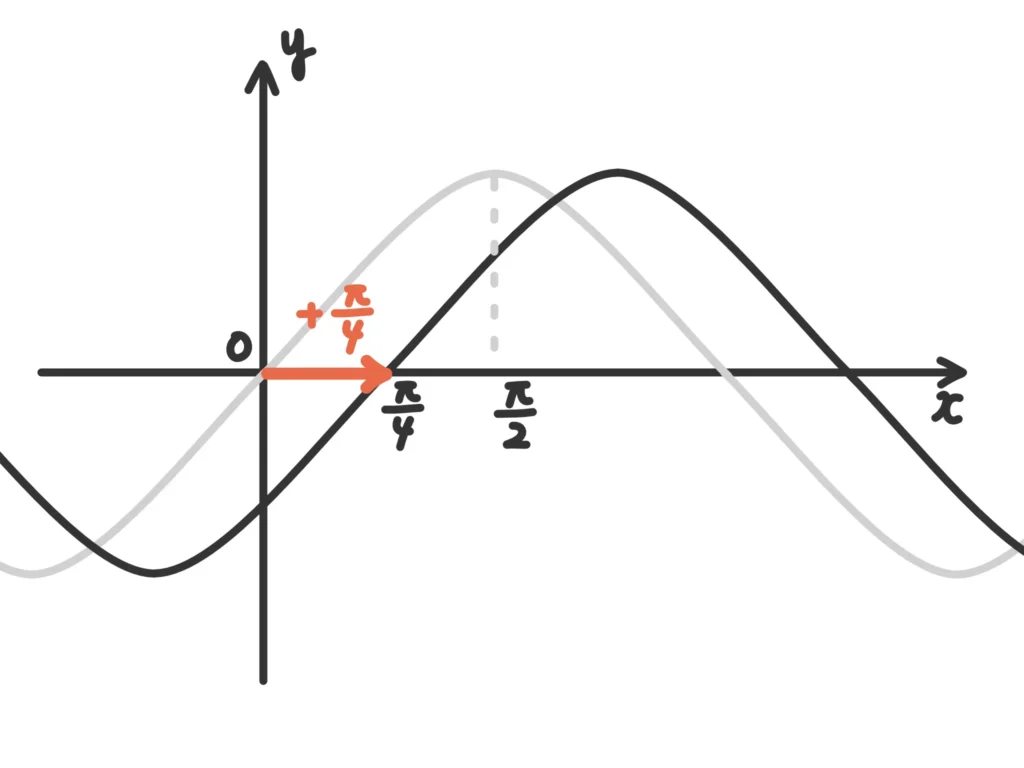
三角・指数・対数関数(数学II)
例えば、三角関数
\(\displaystyle y= \sin\Big(x-\frac{\pi}{4}\Big)\)は\( y=\sin{x}\)を\(x\)軸方向へ\( \displaystyle \frac{\pi}{4} \)平行移動したものとなります。




…ほう。
指数関数の\(y=2^{x-1}+1\)は\(y-1=2^{x-1}\)と変形することで、
\(y=2^x\)の\(x \rightarrow x-1\)、\(y \rightarrow y-1 \)と置き換えた形になる
ので、\(x\)軸方向に\(1\)、\(y\)軸方向に\(1\)だけ平行移動したものになります。
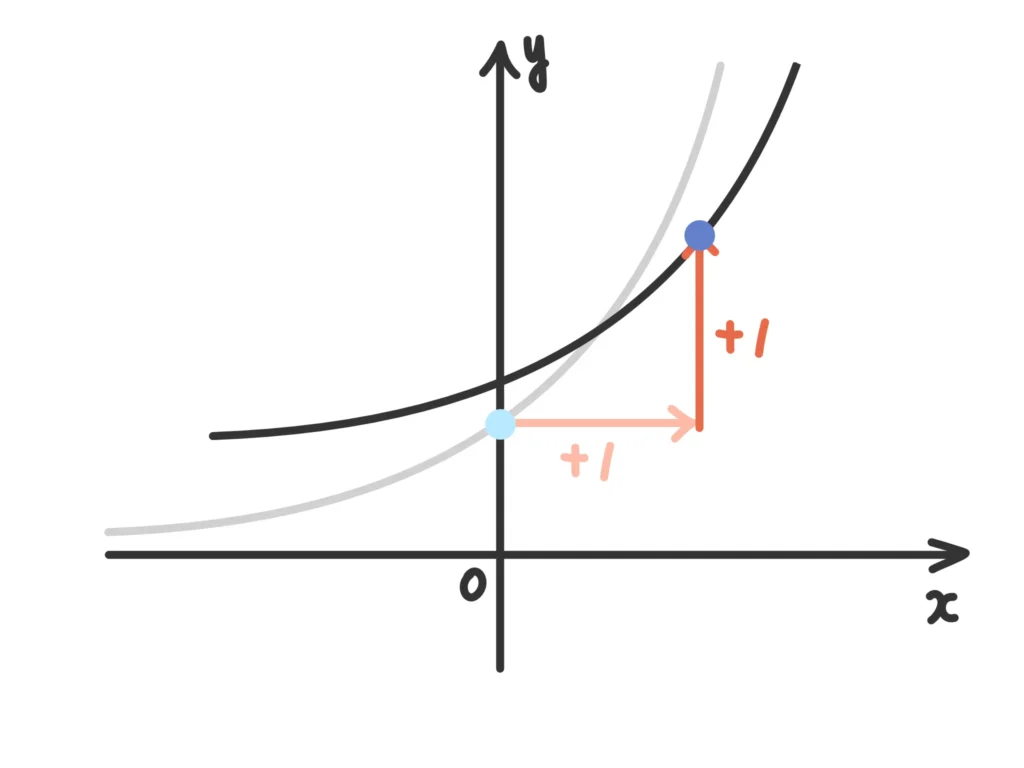




はぁ…。
対数関数の\(y=\log_2(x+1)\)は\(y=\log_2 x\)のグラフを
\(x \rightarrow x+1=x-(-1)\)に置き換えているので、
\(x\)軸方向に\(-1\)だけ平行移動したもの、となります。
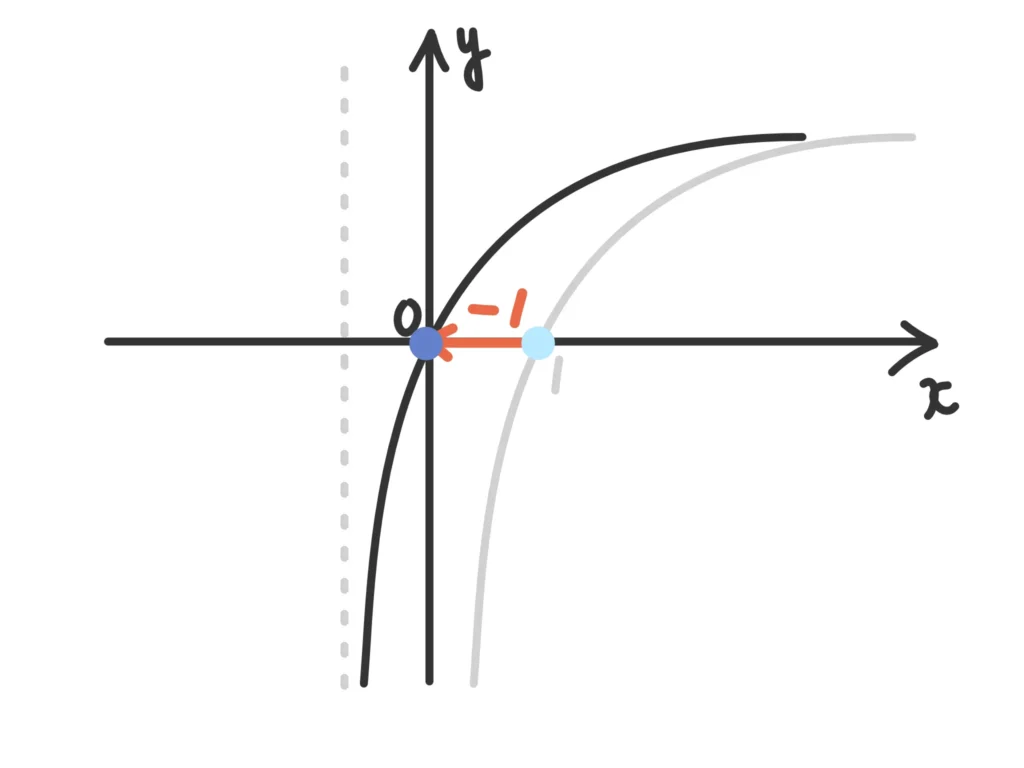




…そろそろよくない?
ちょっとくどいのでそろそろ止めますが、実はまだまだ他にも例があります。
置き換えによる平行移動は便利…というか色んなところに出てくるので慣れていきましょう!
慣れれば二次関数の頂点を読むのもカンタンになります!



数学道は険しい…。
まとめ
結構長くなりましたが、平行移動は実践的にもよく使う手段です。



\(x\)、\(y\)の置き換えで平行移動を表す!
これ大事!






