PR
多項式の割り算総まとめ【筆算から余りの性質、組み立て除法まで全解説!】

多項式の割り算は、筆算がわかれば比較的簡単に理解できます。
ですが、計算をする以上に重要な、押さえておかないといけないポイントがあります。
この記事では多項式の割り算の計算方法から組み立て除法、多項式の割り算の重要な表現方法について説明していきます。
 デカ丸
デカ丸多項式の割り算はただ割ればいいってもんじゃないんですよ
多項式の割り算



さて、今日は多項式の割り算の勉強をしましょう。まぁ、そんなに難しくはないですよ。小学校で習ったわり算の筆算ができれば大丈夫!(チラッ)



ん?今僕のこと見ました?いや、筆算くらいできますよ…。
ということで、多項式の割り算です。
多項式(\(a_n x^n + a_{n-1}x^{n-1} + \cdots + a_1 x + a_0\)の形をした整式)を多項式で割るのは、小学校で習う「筆算」ができれば比較的簡単です。
ただ、この記事の前半は実際に計算してみよう、という話ですが、多項式の割り算で重要なのはココの表現方法です。
ぜひ最後まで読んでみてください!



多項式の割り算は、各次数の項を筆算の各桁のように扱えば大丈夫です!
それでは実際に計算してみましょう!
数学をモチーフにしたオシャレなオリジナルグッズも販売中です!おかげさまで好評頂いてます!
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ!
多項式の割り算の計算方法「筆算」
例1.\(2x^3-3x+12\)を\(2x^2 +4x + 5\)で割る。
コツは抜けている次数の項を空けておく、ということです。



こうすることで計算しやすくなりますし、このあとの「係数のみ」の計算もわかりやすくなります。
(解答)
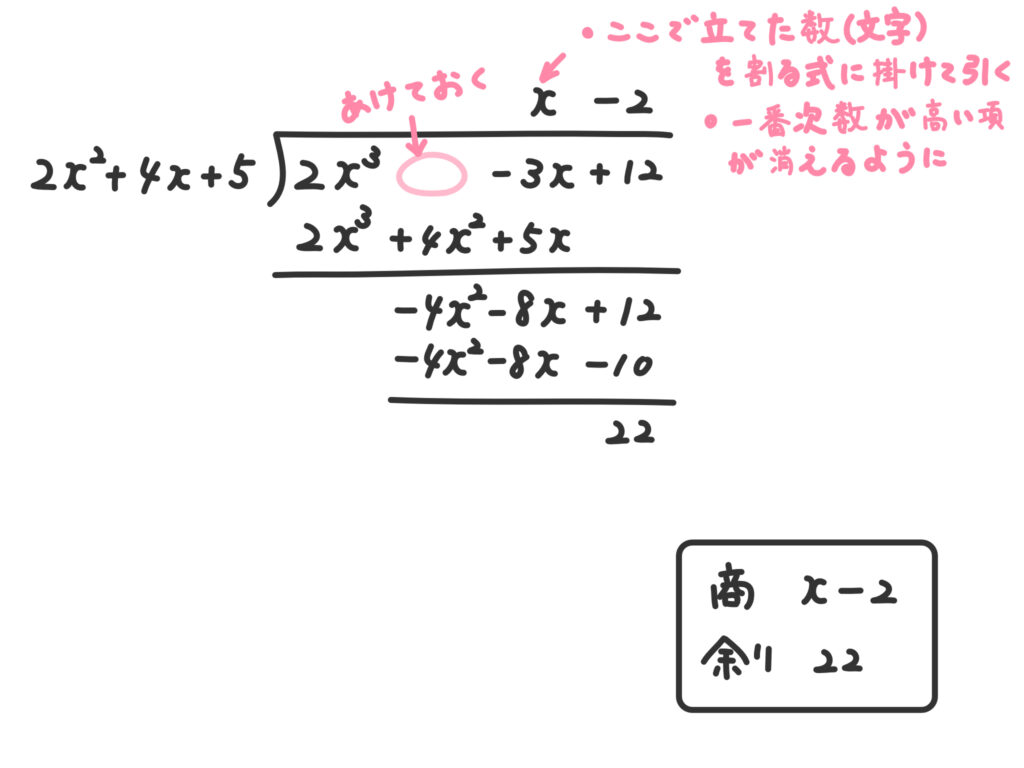

最初は全部書いてもいいですが、ちょっと慣れてくると、\(x\)とか\(x^2\)とかを書くのが面倒になります。実際に計算しているのは係数部分だけだからです。
ということで、できれば係数のみを抜き出して計算するのをオススメします!
このときのコツは、抜けている次数の項は「0」を書いておくことです。
(解答)
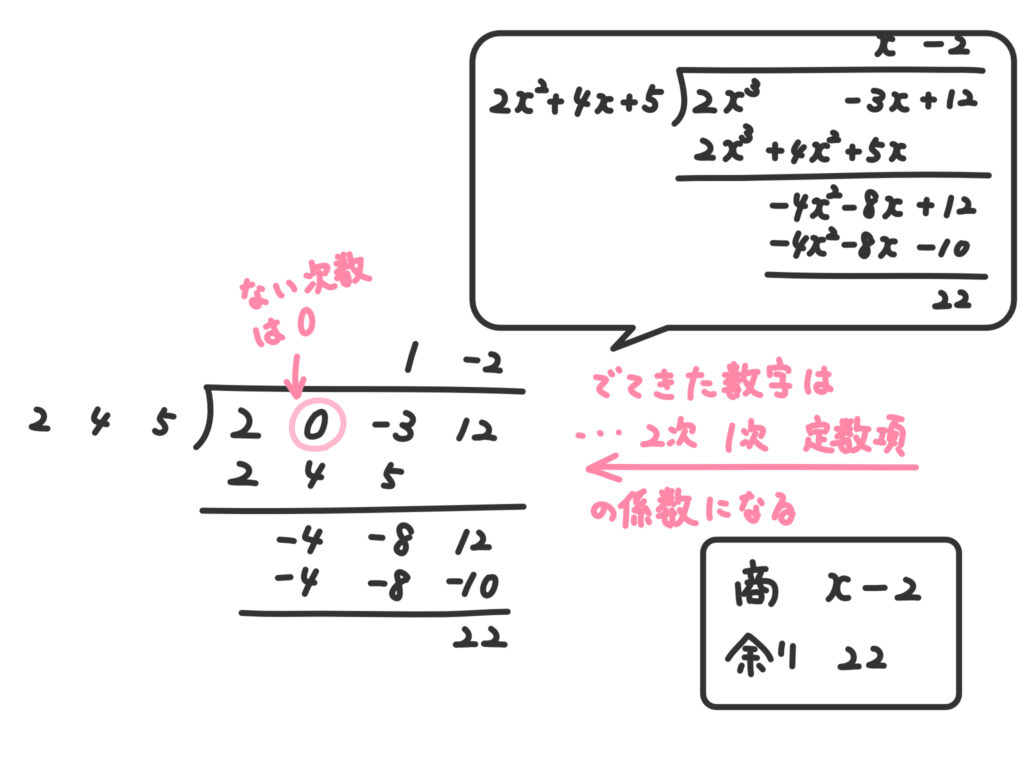

割る式の方に抜けている次数の項があるときも同様です。
例2.\(4x^3 -6x^2 -5\)を\(2x^2+1\)で割る。
(解答)
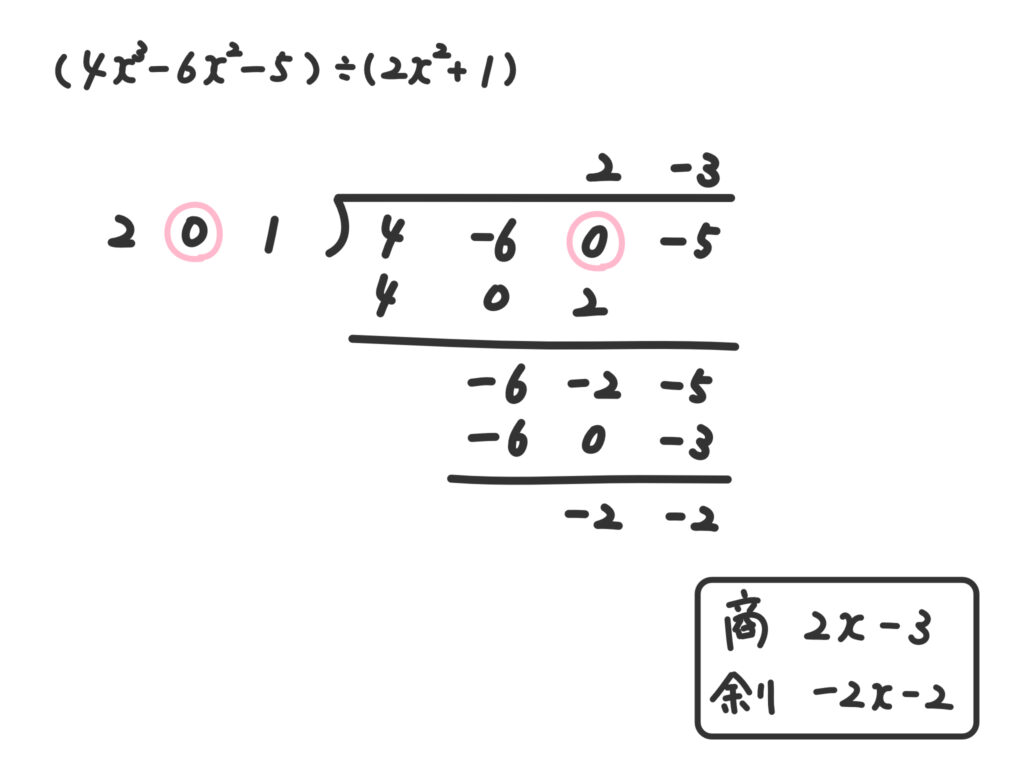




キレイに降べきの順に並べること、抜けている次数の項は係数が0であるとみなして計算すること、が重要です!なんでも整理は大事!
多項式の割り算の計算方法「組み立て除法」
割る式が1次式のときのみ「組み立て除法」という方法が使えます。



えー…これ、ちょっと言葉では説明しにくいんですよね。次の例と図を見ながら実際に手を動かしてみてください!
割る式の\(x\)の係数が\(1\)かそれ以外か、でアプローチの仕方も変わってくるので注意が必要です!
・割る式の\(x\)の係数が\(1\)のとき
例3.\( 2x^3 -x^2 -2x -8\)を\(x-2\)で割る。
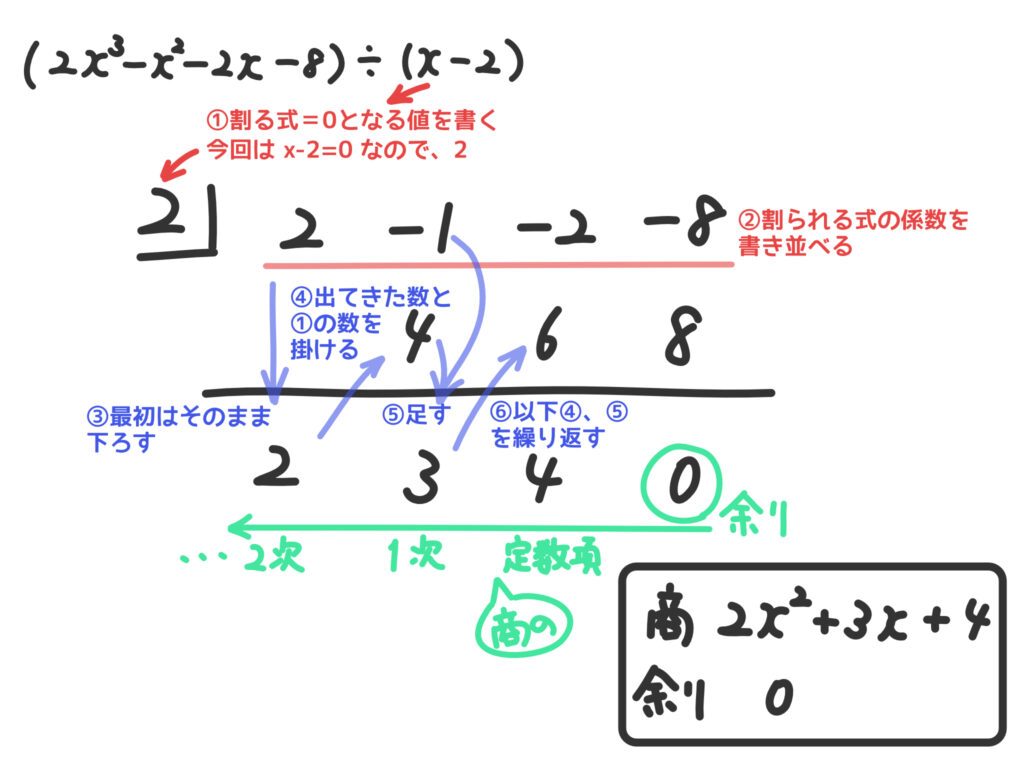

こんな感じで割ってくれればOKです。
・割る式の\(x\)の係数が\(1\)以外のとき
割る式の\(x\)の係数が\(1\)以外のときも同様に計算ができますが、最後に調整が必要です。
例4.\( 3x^3 -x^2 +6x +3\)を\(3x-1\)で割る。
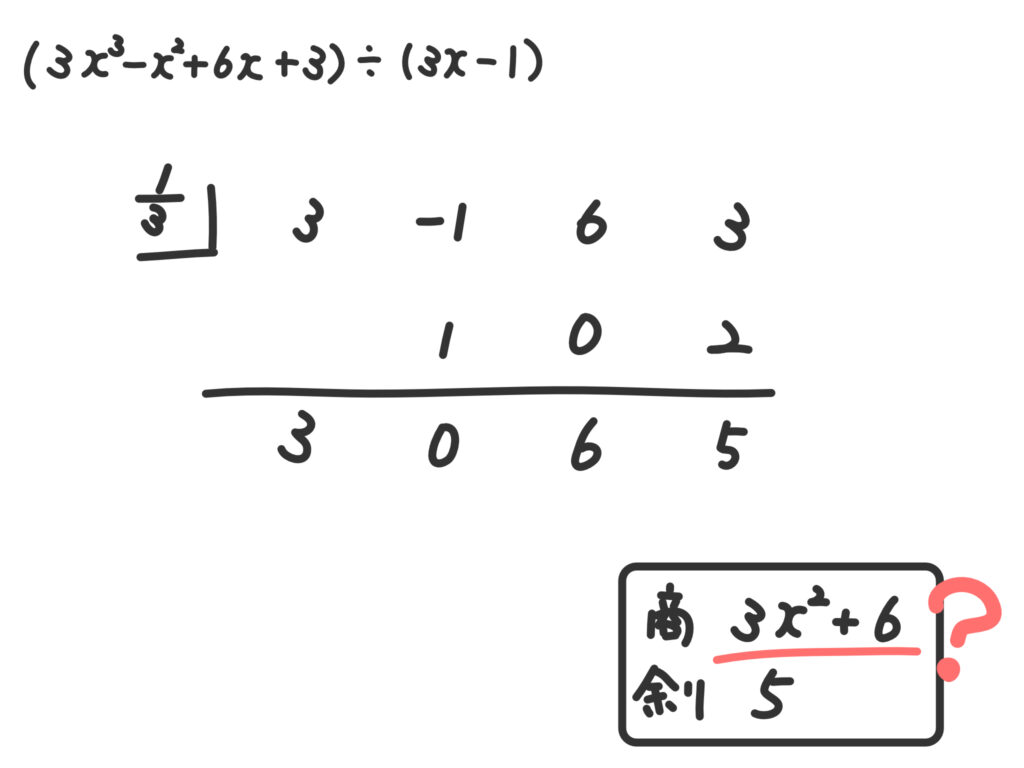
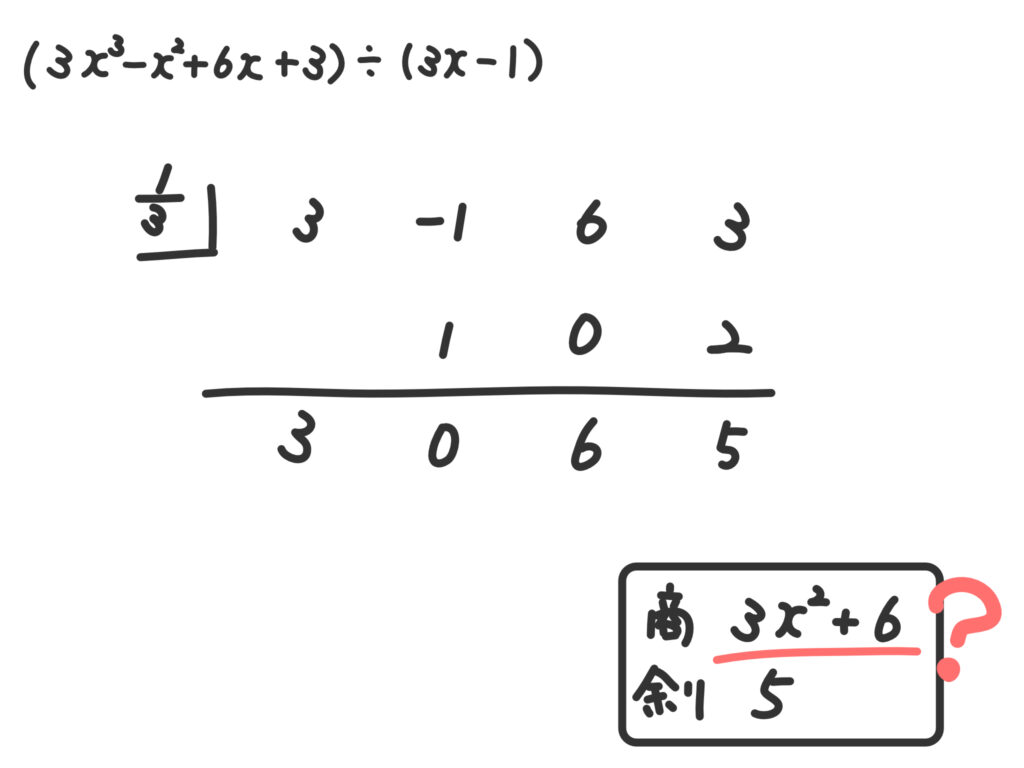
このときの組み立て除法の注意点としては、\(3x-1\)ではなく、\(\displaystyle x-\frac{1}{3} \)で割ったことになる、という点です。
つまり、このあと出てくる(元の式)=(割る式)×(商)+(余り)の形で表すと、
\(\displaystyle 3x^3 -x^2 +6x +3 = (x-\frac{1}{3})(3x^2 + 6) + 5\)
を計算したことになります。
当然\(3x-1\)で割った形になっていないので、修正が必要です。
ではどうするか?というと、\(\displaystyle x-\frac{1}{3} \)から\(\displaystyle \frac{1}{3}\)をくくり出します。その上で、商を調整します。
\(\displaystyle 3x^3 -x^2 +6x +3 = \frac{1}{3}(3x-1)(3x^2 + 6) + 5\)
\(\displaystyle \quad = (3x-1) \{ \frac{1}{3}(3x^2 + 6) \} + 5\)
\(\displaystyle 3x^3 -x^2 +6x +3 = (3x-1)(x^2 + 2) + 5\)
よって、商\(x^2+2\)、余りは\(5\)となります。



組み立て除法は3次式以上の因数分解をするためによく使いますが、割る式の\(x\)の係数が\(1\)以外のときは「どんな式で割ってやったのか?」という点を意識しないと間違えやすいですね。
組み立て除法ってどうなってるの?という仕組み



例3を、普通の割り算と組み立て除法を比較しながら計算してみましょう。
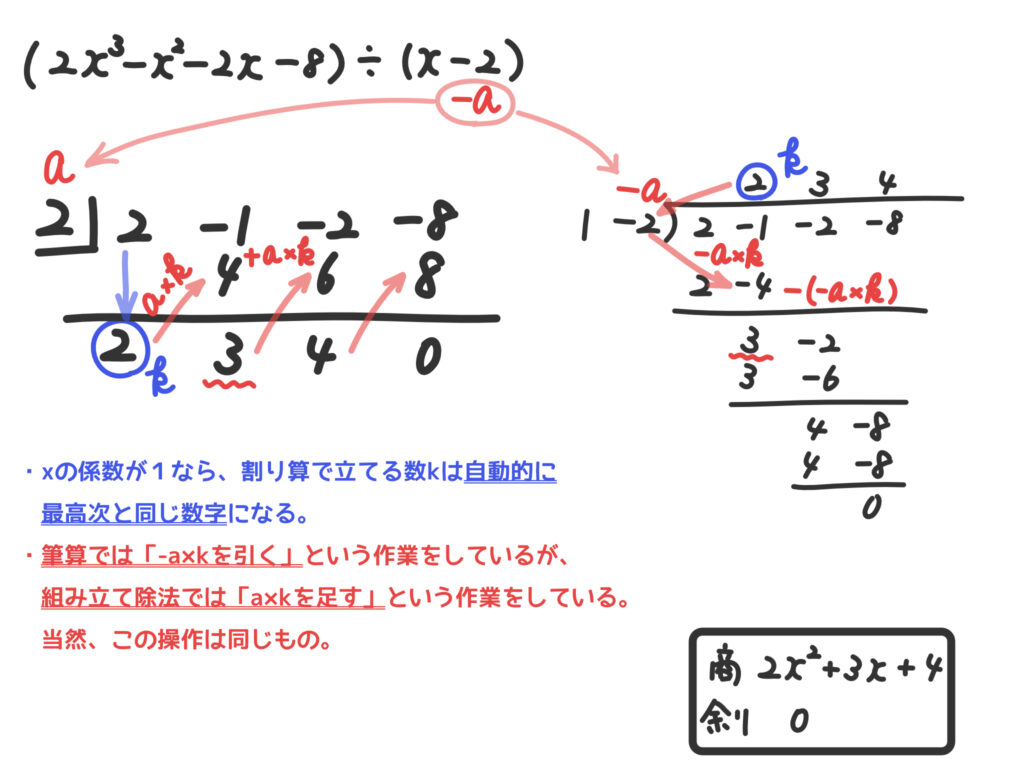

多項式の割り算は商と余りでこう表現する
多項式の割り算で重要なのは次の表現方法です。
多項式の割り算の商と余りを使った表し方
多項式\(P(x)\)を多項式\(A(x)\)で割ったとき、商が\(Q(x)\)、余りが\(R(x)\)であったとする。
このとき、
\(P(x) = A(x) Q(x) +R(x)\)
(元の式)=(割る式)×(商)+(余り)
と表すことができる。ただし、
(余り\(R(x)\)の次数)<(割る式\(A(x)\)の次数)
となる。



これも例を見ながら確認してみましょう!
例1.\(2x^3-3x+12\)を\(2x^2 +4x + 5\)で割る。
商が\(x-2\)、余りが\(22\)なので、
\(2x^3-3x+12 = (2x^2 +4x + 5)(x-2) + 22\)
と表すことができます。
意外と重要なポイントは(余り\(R(x)\)の次数)<(割る式\(A(x)\)の次数)という点です。
これは普通の数でも言えることです。
例.\(10 \div 3=3あまり1\)
(元の式)=(割る式)×(商)+(余り)を数で言い換えると、(元の数)=(割る数)×(商)+(余り)と変形できる、ということになります。
\(10 = 3 \times 3 + 1\)
このとき、最後の1を見れば「3で割った余り1」というのがわかります。
ただ、同じ等式でも、
\(10 = 3 \times 2 + 4\)
と、変形することもできますが、この4を見て「3で割った余り4」というのはおかしいですよね?
これは、余り(に見える)4はまだ3で割ることができるからです。余りがまだ割る数で割れるなら、限界まで割らないといけない、ということなんですね。
\(4 = 3 \times 1 + 1\)
つまり、
\(10 = 3 \times 2 + 3 \times 1 + 1\)
として「3で割った余りは1」と見ます。



割れる限界まで割る!当たり前に聞こえますが重要なポイントです!
なぜこの形が重要かというと、このあと出てくる剰余の定理や因数定理のイメージに繋がるからです。
剰余の定理や因数定理が苦手な人が結構いるのですが、それはこの
(元の式)=(割る式)×(商)+(余り)
の形がアタマの中に入っておらず、定理の式だけを見てどうにか覚えたり使ったりしようとするからですね。
また、多項式の割り算で余りを求める、という定番の問題でもこの形が重要になってきます。



「式が割り切れる」ことや「余りがどこから出てくるか?」などの本質を理解するためにもこの形は大事です!
数学をモチーフにしたオシャレなオリジナルグッズも販売中です!おかげさまで好評頂いてます!
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ!
多項式の割り算の練習問題
問.\(P(x) = x^4 + x^3 – 6 x^2 + 2x + 9\)について、
(1) \(P(x)\)を\((x+1)(x-1)(x+3)\)で割った余りを求めよ。
(2) \(P(x)\)を\((x-1)(x+3)\)で割った余りを求めよ。
(3) \(P(x)\)を\(x+3\)で割った余りを求めよ。
答え
(1) \(x^2 + 3x + 3\)
(2) \(x+6\)
(3) \(3\)
多項式の割り算まとめ
多項式の割り算についてでした。
計算方法と、組み立て除法はこのあと使うので、テクニックとして押さえておいて下さい。
ただ、もっと重要なのは
(元の式)=(割る式)×(商)+(余り)
の形をアタマの中に入れておくことです。



これはぜひ押さえておいて下さい!






