PR
ガウス積分の証明【重積分やベータ関数とガンマ関数の関係を使った証明】

この記事ではガウス積分という有名な積分の計算をしていきます。
ガウス積分は正規分布の確率密度関数を求めるときや、物理なんかでも使われる(らしい)、とても応用のきく積分です。
 せんせ
せんせ結果は覚えておいてソンはないと思います。
ちょっと高校範囲は逸脱しますが、標準正規分布の確率密度関数はなぜあんな形をしているのか?という話にも関わってきます。高校の教科書では「こうなる!」としか書いていないので、「標準正規分布の確率密度関数ってなんであんな形なの?」と思っている人は、少しずつ読み進めて理解してもらえれば、と思います。
この記事ではガウス積分の計算方法2パターンの解説と、おまけで標準正規分布との関わりについても少し紹介したいと思います。
ガウス積分とは?
そもそもガウス積分とは、次の積分の結果のことをいいます。
ガウス積分
\(\displaystyle \int_{-\infty}^{\infty}e^{-ax^2}dx=\sqrt{\frac{\pi}{a}}\)
特に\(a=1\)のとき、
\(\displaystyle \int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi}\)
積分区間が\((-\infty, \infty)\)となっていますね。
これは広義積分といわれるもので、ざっくり説明すると、グラフが切れている部分や\(\infty\)など普通の定積分では計算できない積分区間を、極限を取ることで計算する、という方法です。



もちろん、広義積分は収束したり発散したりします。収束する場合に、それを広義積分の値にしましょう、ということですね。
無限級数の「部分和→極限をとる」という話と考え方は似てます。
それでは、ガウス積分の証明をしていきましょう!
ガウス積分の証明
以下では\(\displaystyle \int_{-\infty}^{\infty}e^{-ax^2}dx=\sqrt{\frac{\pi}{a}}\)の証明をしていきます。
重積分を使った証明
「重積分」という2変数関数の積分を使っていきます。重積分の説明はこちらでしています。
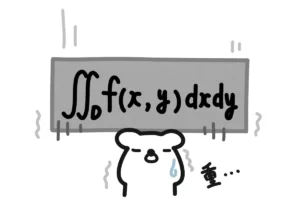




重積分は高校数学の範囲を超えますが、数学IIIの積分をしていれば、そんなに難しい考え方では無いです。2変数を順番に積分するよ、という話です。
ただ、計算上「重積分の置換積分とヤコビアン」という話が出てくるので、これはちょっとサクッと理解するのは大変かもしれません…。



まぁ、「そうなるんだぁ…」くらいに思っていただいても問題はないです。余裕があるときにこちらを読んで理解してもらえれば、と思います。
ヤコビアンのイメージを図にしているので、わかりやすいとは思いますよ。


【重積分を使った証明】
\(\displaystyle I = \int_{-\infty}^{\infty}e^{-ax^2}dx\)とおく。
\(\displaystyle I = \int_{-\infty}^{\infty}e^{-ay^2}dy\)としてもう一つ\(I\)を準備した上で、
\(\displaystyle I^2 = \int_{-\infty}^{\infty}e^{-ax^2}dx\int_{-\infty}^{\infty}e^{-ay^2}dy\)
\(\displaystyle \quad = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-a(x^2+y^2)}dxdy \)
ここで、\(x=r \cos\theta\)、\(y=r \sin\theta\)と極座標変換すると、ヤコビアンは\(||J|| = r\)なので(ヤコビアンの説明はこちらの記事を参照)、
\(dxdy = rdrd\theta\)
また、\( \{ x: -\infty \to \infty , y: -\infty \to \infty \} \)の表す領域は\( \{ r: 0 \to \infty , \theta: 0 \to 2\pi \} \)となるので、
\(\displaystyle \quad = \int_{0}^{\infty}\int_{0}^{2\pi} e^{-ar^2}rdrd\theta \)
\(\displaystyle \quad = \int_{0}^{\infty}e^{-ar^2}rdr \int_{0}^{2\pi} d\theta \)
\(\displaystyle \quad = \left[-\frac{1}{2a}e^{-ar^2} \right]_{0}^{\infty} \left[\theta \right]_{0}^{2\pi}\)
\(\displaystyle \quad = \frac{1}{2a}\cdot 2\pi=\frac{\pi}{a}\)
よって、\(\displaystyle I=\sqrt{\frac{\pi}{a}}\)すなわち、 \(\displaystyle \int_{-\infty}^{\infty}e^{-ax^2}dx=\sqrt{\frac{\pi}{a}}\)(終)
ベータ関数とガンマ関数の関係を使った証明方法



ベータ関数とガンマ関数の関係式を使います。
ベータ関数とガンマ関数の関係
\(p>0,q>0\)とすると、
\(\displaystyle B(p,q)=\frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)}\)
の関係が成り立つ。ただし、\(B(p,q)\)、\( \Gamma(p)\)はそれぞれベータ関数、ガンマ関数で、
\(\displaystyle B(p, q) = \int_0^1x^{p-1}(1-x)^{q-1} dx \)
\(\displaystyle \Gamma (p) = \int_0^\infty t^{p-1} e^{-t} dt \)
という関数です。
あと、こちらの記事でも説明していますが、\(\displaystyle B \left( \frac{1}{2}, \frac{1}{2} \right) = \pi \)という計算結果も使います。



まぁ、このベータ関数とガンマ関数の関係式を求めるためには重積分とその置換を使います。なので、元をたどってしっかり証明しようとすると、結局重積分とその置換の知識がいるんですけどね…。
こういう関係式があるんだよ、というのを認めてあげれば、証明は結構簡単です!
【ベータ関数とガンマ関数の関係を使った証明】
\(\displaystyle B\left( \frac{1}{2}, \frac{1}{2} \right) = \frac{\Gamma\left( \frac{1}{2} \right)\Gamma\left( \frac{1}{2} \right)}{\Gamma(1)}\)
\(\displaystyle \pi = \left\{ \Gamma\left( \frac{1}{2} \right) \right\}^2 \)…※(←ちなみに、\(\Gamma(1)=1\)です。こちらの記事を参照。)
ここで、\(\displaystyle \Gamma\left( \frac{1}{2} \right) \)について
\(\displaystyle \Gamma\left( \frac{1}{2} \right) = \int_0^\infty t^{-\frac{1}{2}} e^{-t} dt \)なので、
\(t=ax^2\)とおくと、\(t:0 \to \infty\)のとき\(x:0 \to \infty\)、
\(dt = 2axdx\)
よって、
\(\displaystyle \Gamma\left( \frac{1}{2} \right) = \int_0^\infty a^{-\frac{1}{2}}x^{-1} e^{-ax^2} 2axdx \)
\(\displaystyle \quad = 2 \int_0^\infty a^{\frac{1}{2}} e^{-ax^2} dx \)
\(\displaystyle \quad = \sqrt{a} \int_{-\infty}^\infty e^{-ax^2} dx \)(←\(e^{-ax^2}\)は偶関数だから)
ゆえに、※より、
\(\displaystyle \pi = \left\{ \sqrt{a} \int_{-\infty}^\infty e^{-ax^2} dx \right\}^2 \)
\(\displaystyle \int_{-\infty}^{\infty}e^{-ax^2}=\sqrt{\frac{\pi}{a}} \)(終)
おまけ.標準正規分布が確率密度関数になっていることの確認
標準正規分布の確率密度関数は、
\(\displaystyle f(X)=\frac{1}{\sqrt{2\pi}}e^{-\frac{X^2}{2}}\)
で与えられます。これが確率密度関数の条件を満たしていることを確認しましょう!



要はとりうる確率変数で積分すると、「1」になっていないとダメです。全事象の確率は「1」ですからね。
(確認)
\(\displaystyle \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{X^2}{2}}dX=1\)となることを確認する。
\(X = \sqrt{2}t\)とおくと、\(X: -\infty \to \infty \)のとき\(t: -\infty \to \infty \)、
\(dX = \sqrt{2}dt\)
よって、
\(\displaystyle \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{X^2}{2}}dX=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-t^2}\sqrt{2}dt\)
\(\displaystyle \quad = \frac{1}{\sqrt{\pi}} \int_{-\infty}^{\infty}e^{-t^2}dt\)
\(\displaystyle \quad = \frac{1}{\sqrt{\pi}} \cdot \sqrt{\pi} = 1 \)
したがって、\(\displaystyle f(X)=\frac{1}{\sqrt{2\pi}}e^{-\frac{X^2}{2}}\)は確率密度関数の条件を満たす。



まとめ
ガウス積分の計算についての説明、でした。
ガウス積分は重積分と置換積分が必要なので、実際には計算が結構大変です。
「こんな計算があるんだなぁ…」くらいの理解でもいいかもしれませんが、覚えておいてソンはない計算です!
余裕があれば少しずつ理解していきましょう。



重積分の練習にはなりますが…。
高校生の知識としては「なんで標準正規分布の確率密度関数ってあんな形なの?」という疑問の解決にはなるかな、と思います。







