PR
標準正規分布とは【正規分布との関係と標準正規分布表の見方を丁寧に説明】
こちらの記事で、世の中の現象は「二項分布」や「正規分布」と見なせるものが多い、という話をしました。

ですが、「二項分布」や「正規分布」はそのままでは計算しづらいので、標準正規分布に変換(標準化)して確率を求めたり、推定や検定を行っていきます。
この記事では、標準正規分布の説明と、正規分布との関係、標準正規分布表の見方・使い方についてまとめていきます。
 せんせ
せんせ今回はテクニック的なお話がほとんどです。でも、この「標準正規分布に変換して作業をする」という操作はかなり重要ですので押さえておいてください。
そもそも標準正規分布とは?
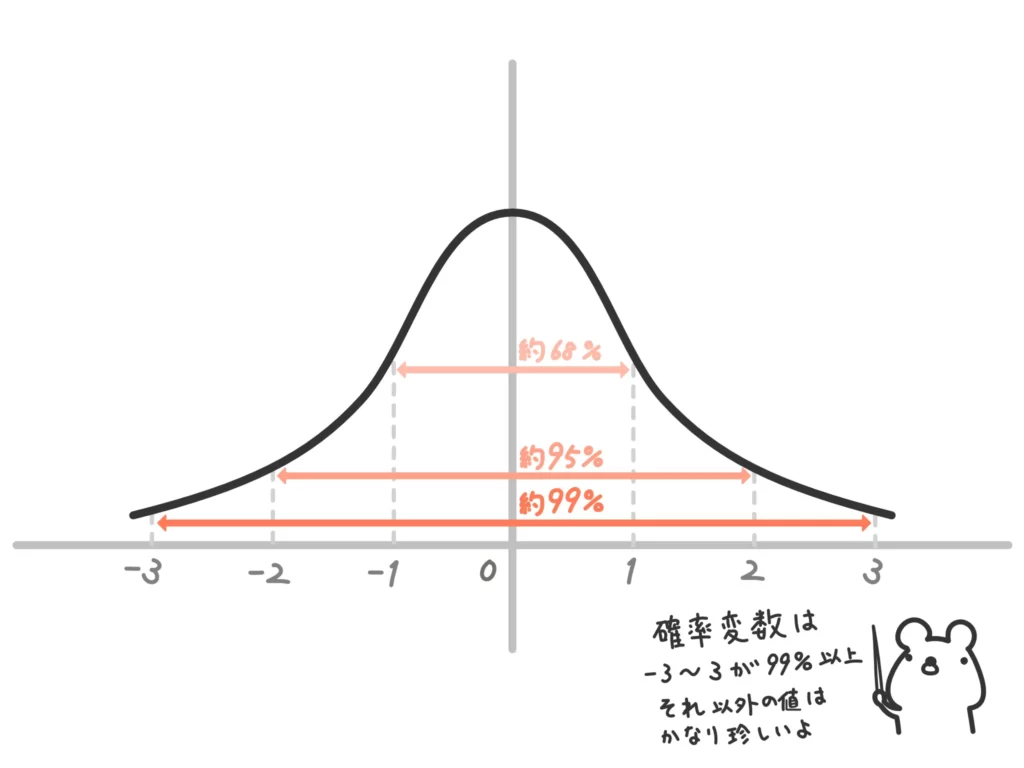
標準正規分布は平均0、分散1の正規分布のことです。
つまり、\(N(0,1)\)のことですね。山がちょうど0のところにきます。




ちなみに確率密度関数は次のようになりますが、正規分布同様、こちらも覚えなくて大丈夫です。
標準正規分布の確率密度関数\(f(X)\)は、
\(\displaystyle f(X)=\frac{1}{\sqrt{2\pi}}e^{-\frac{X^2}{2}}\)
正規分布\(N(m,\sigma ^2)\)の確率密度関数\(\displaystyle f(X)=\frac{1}{\sqrt{2\pi \sigma ^2}}e^{-\frac{(X-m)^2}{2\sigma ^2}}\)を\(m=0\)、\(\sigma = 1\)にしたものですね。
重要なことは、この標準正規分布が「平均0、分散1」でバランスよく固定された、とても都合のいい形だ、ということですね。
そして、この標準正規分布がとる確率は既に調べられていて、表になっています。



後ほど紹介しますが、この表は2種類あります。
つまり、「ある正規分布に従う確率変数について調べたい!」というときには、以下の流れで標準正規分布を利用していきます。
「正規分布を標準正規分布に変換(標準化)」→「標準正規分布表を使って、確率を求めたり推定や検定を行う」



元の正規分布の確率変数が標準正規分布でどの確率変数に相当するか変換(標準化)して標準正規分布上で色々調べるんですね。
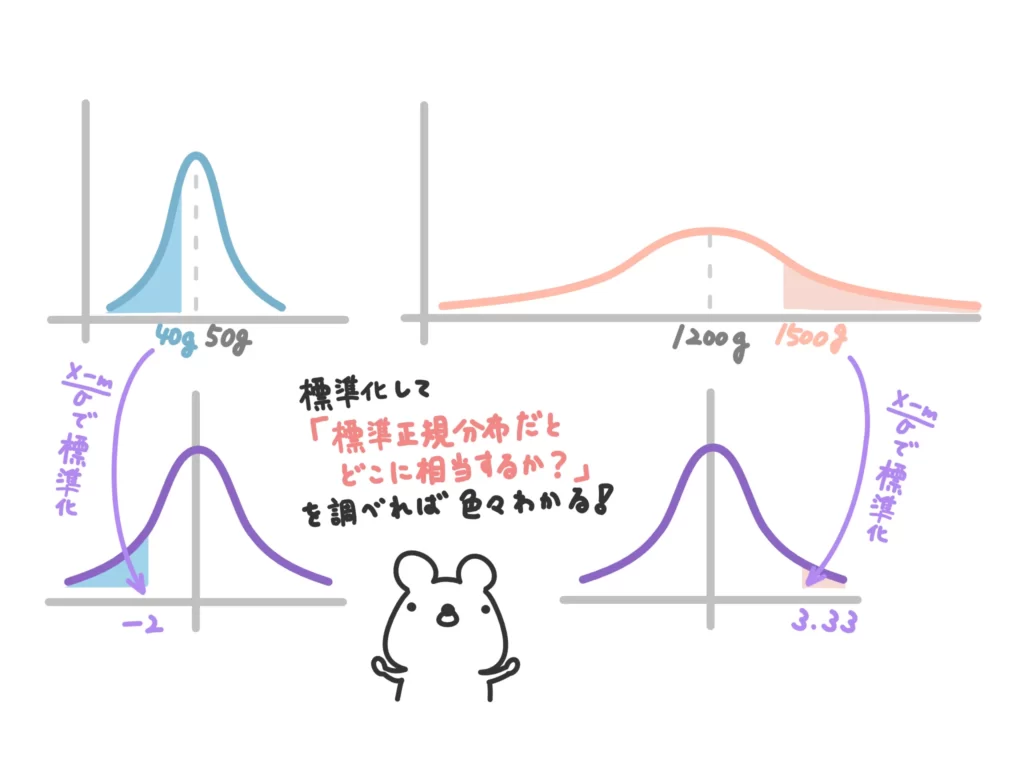

正規分布を標準化する
では、正規分布に従う確率変数\(X\)を標準正規分布に従うように変数変換、つまり標準化します。



いきなりですが、この変換、超重要です!
絶対押さえておいてください!
確率変数\(X\)が平均\(m\)、分散\(\sigma ^2\)の正規分布に従うとき、つまり確率変数\(X\)が正規分布\(N(m, \sigma ^2)\)に従うとき、
\(\displaystyle Z=\frac{X-m}{\sigma}\)
と確率変数\(X\)を\(Z\)に変数変換すれば、\(Z\)は標準正規分布に従う。
※ 間違えやすいですが、分母にくるのは\(\sigma\)、つまり標準偏差、です!「標準化だから標準偏差」とかこじつけでもいいので間違えずに覚えてください!
この変数変換で、正規分布\(N(m,\sigma)\)に従う\(X\)が、平均0・分散1の変数\(Z\)になります!



変数変換によって平均・分散がどのように変換されるか?というのがわかっていれば、平均が\(m \rightarrow 0\)、分散が\(\sigma^2 \rightarrow 1\)になるのがわかるはずです。



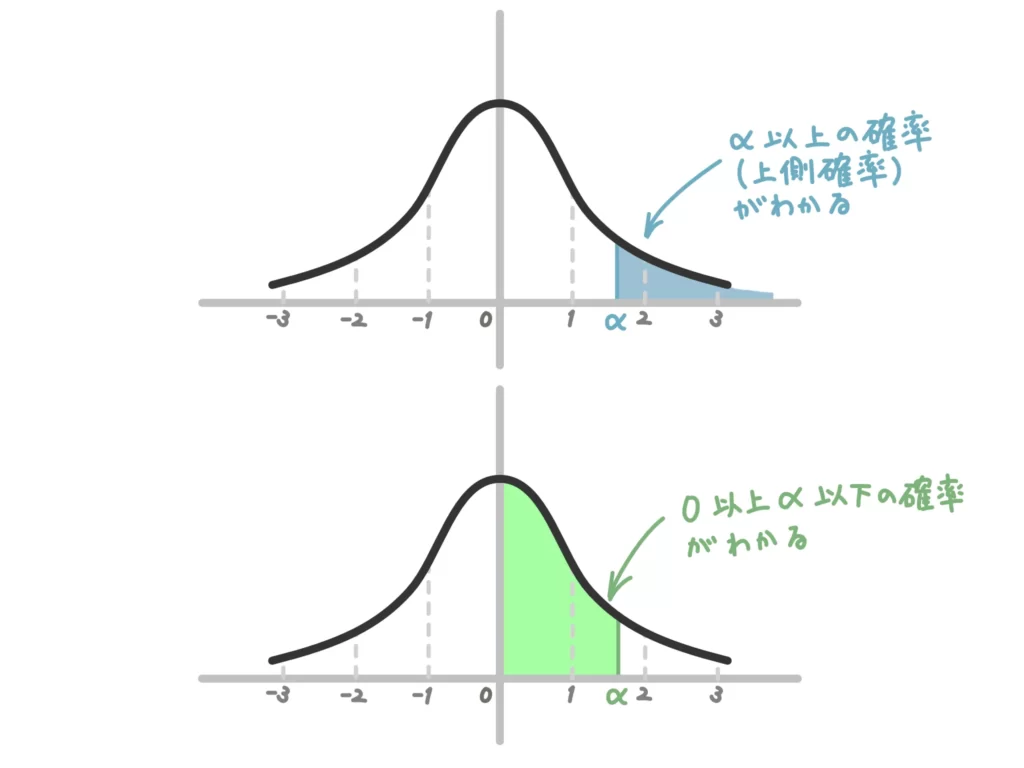
標準正規分布表の見方
正規分布を標準化したら、標準正規分布表を使って確率を求める作業などをしていきます。
標準正規分布表は2種類あります。

また、標準正規分布は左右対称なので、0以上の確率変数(分布の山の右側の裾)のみ与えられます。0以下の確率変数はひっくり返したときに該当する0以上の確率変数を使って読んでいきます。
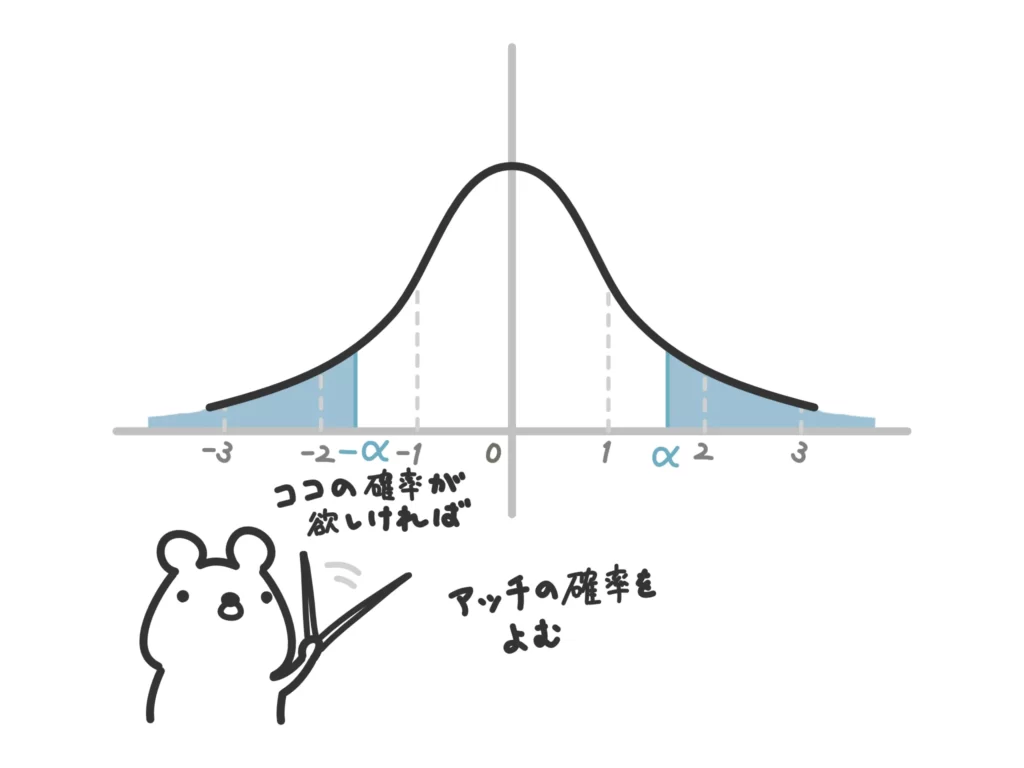

あとは、パズルのように確率を足し引きしながら欲しい確率を求めていきます。



それでは具体的な標準正規分布表の読み方を確認しましょう!
例.あるドーナツ屋さんのドーナツの重さは、平均50g、分散10です。このドーナツ屋さんでドーナツを1つ買ったときに55g以上である確率はいくらでしょう?
(解答)
欲しい確率はこの部分ですね。
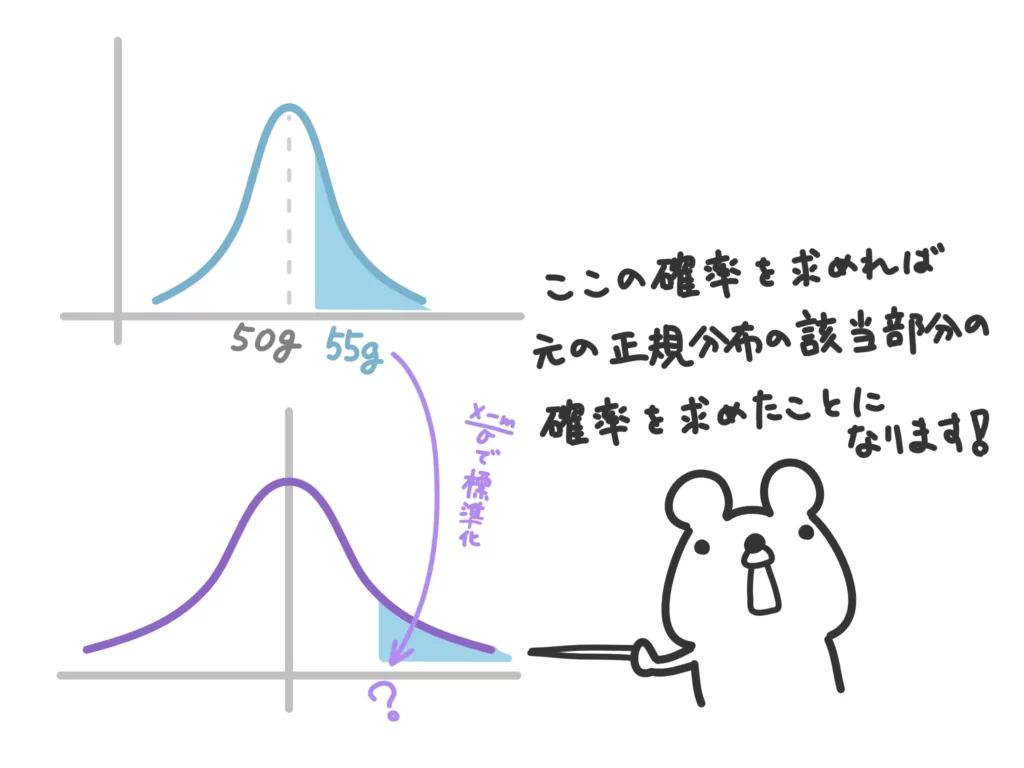




まずはデータを標準化します。
55gという境目が標準正規分布の変数でいくらに相当するか?を計算します。
\(\displaystyle Z=\frac{55-50}{\sqrt{10}}=1.58\cdots \)
この1.58を小数第1位までと小数第2位に分けます。1.5と0.08ですね。
これで、表のクロスした部分を読みます。
① \(\alpha\)〜の確率が求められる表(上側確率表)の場合



統計検定や一般的にはこちらのタイプの標準正規分布表が多いです。
| .00 | .01 | … | .08 | .09 | |
| 0.0 | 0.5000 | 0.4960 | … | 0.4681 | 0.4641 |
| 0.1 | 0.4602 | 0.4562 | … | 0.4286 | 0.4247 |
| … | … | … | … | … | … |
| 1.1 | 0.1357 | 0.1335 | … | 0.1190 | 0.1170 |
| 1.2 | 0.1151 | 0.1131 | … | 0.1003 | 0.0985 |
| 1.3 | 0.0968 | 0.0951 | … | 0.0838 | 0.0823 |
| 1.4 | 0.0808 | 0.0793 | … | 0.0694 | 0.0681 |
| 1.5 | 0.0668 | 0.0655 | … | 0.0571 | 0.0559 |
| … | … | … | … | … | … |
| 3.0 | 0.0013 | 0.0013 | … | 0.0010 | 0.0010 |
今回の標準正規分布表は\(\alpha\)〜の確率が得られるので、そのまま読んだ0.0571=5.71%が答えになります。
② 0〜\(\alpha\)の確率が求められる表の場合



高校の教科書や共通テストはこのタイプの標準正規分布表が多いですね。
得られる確率は違いますが、読み方は同じです!
| .00 | .01 | … | .08 | .09 | |
| 0.0 | 0.0000 | 0.0040 | … | 0.0319 | 0.0359 |
| 0.1 | 0.0398 | 0.0438 | … | 0.0714 | 0.0753 |
| … | … | … | … | … | … |
| 1.1 | 0.3643 | 0.3665 | … | 0.3810 | 0.3830 |
| 1.2 | 0.3849 | 0.3869 | … | 0.3997 | 0.4015 |
| 1.3 | 0.4032 | 0.4049 | … | 0.4162 | 0.4177 |
| 1.4 | 0.4192 | 0.4207 | … | 0.4306 | 0.4319 |
| 1.5 | 0.4332 | 0.4345 | … | 0.4429 | 0.4441 |
| … | … | … | … | … | … |
| 3.0 | 0.4986 | 0.4986 | 0.4989 | 0.4990 |
これで、0.4429という値は求められましたが、これはあくまで0〜1.58までの確率です。
欲しいのは55g以上、つまり標準正規分布では1.58以上の部分の確率です。



ここで作業が必要になります。
標準正規分布表で与えられているのは標準正規分布の右半分なので、この右全体の確率は0.5です(全体の確率は1で、標準正規分布は左右対称だから、確率はちょうど半分)。実際に3.09(表の一番右下)の確率を読むと0.4990とほぼ0.5に近い値になっています。
つまり、1.58以上の部分が欲しければ、0.5から先ほど読んだ0.4429を引けばいい、ということになります。
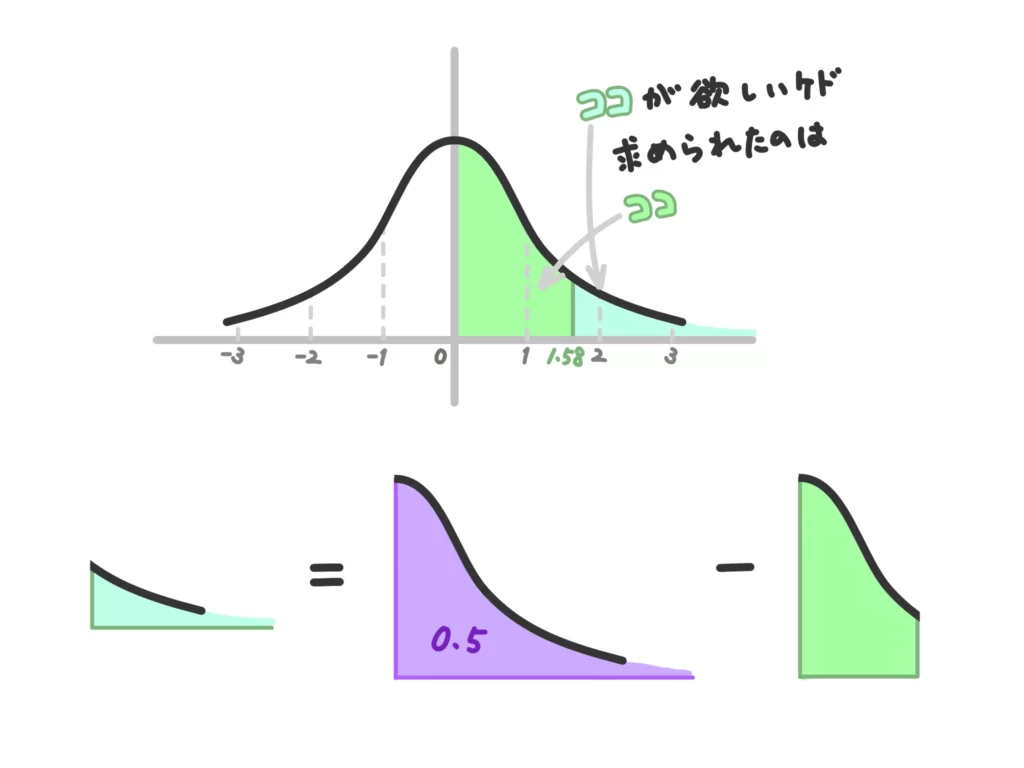

0.5-0.4429=0.0571。5.71%、となります。先ほどの答えと一致しましたね!
ということで、重要なポイントは「どこの確率が欲しいのか?」「与えられた標準正規分布表でどのように読むか?場合によっては計算操作が必要か?」を考えて臨機応変に対応することです。
ちなみに、スプレッドシートで標準正規分布表を作ってみましたので、使いたい人はどうぞ!PDF形式です。
標準正規分布表(上側確率)・標準正規分布表(教科書・共通テストの形式)
まとめ
標準正規分布と標準正規分布表の使い方の説明でした。
標準正規分布表の使い方はもちろん重要ですが、その前の標準化の式、
\(\displaystyle Z=\frac{X-m}{\sigma}\)
は色々なところに顔を出すのでしっかり押さえていきましょう。
正規分布から標準正規分布に標準化して確率を求めたり推定をすることはよくあるので、まずはこの標準正規分布に慣れていきましょう!