正規分布とは？【例もあげながら統計初心者でもわかりやすく丁寧に説明！】

正規分布…統計ではずせない確率分布の一つです。

簡単に説明すると、真ん中の確率が大きく、左右対称に広がっていく確率分布のことです。

という人のために、この記事では正規分布で押さえておくべき点について説明していきます。

正規分布とは？

ということで、今回のテーマは正規分布です。世の中の様々な現象はこの正規分布に従うことが多いです。ドーナツの重さも（恐らく）正規分布に従います。

この正規分布、平均が山の頂上にきていて、その山から離れるほど確率が０に近づく、左右対称の確率密度関数をもつ分布です。

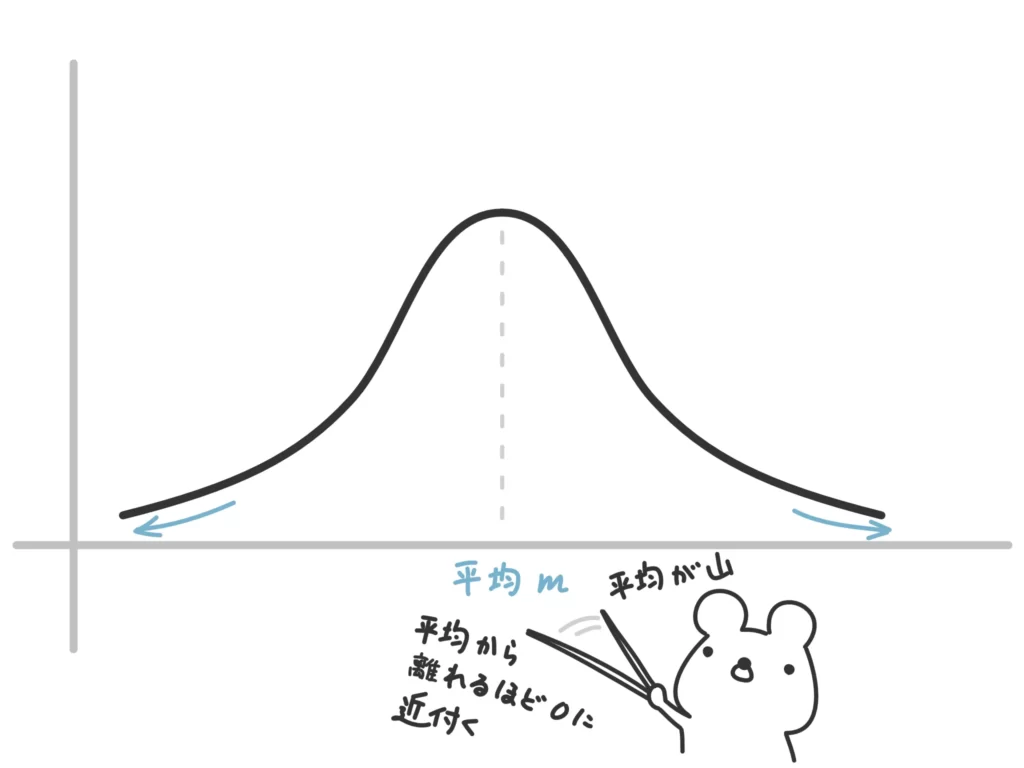
いわゆる「釣鐘（つりがね）型」と言われる形です！あまり釣鐘には見えませんが！

とてもシンプルで自然な確率密度関数ですね。平均の確率変数の確率が一番大きく、そこから離れるにつれて確率が小さくなります。

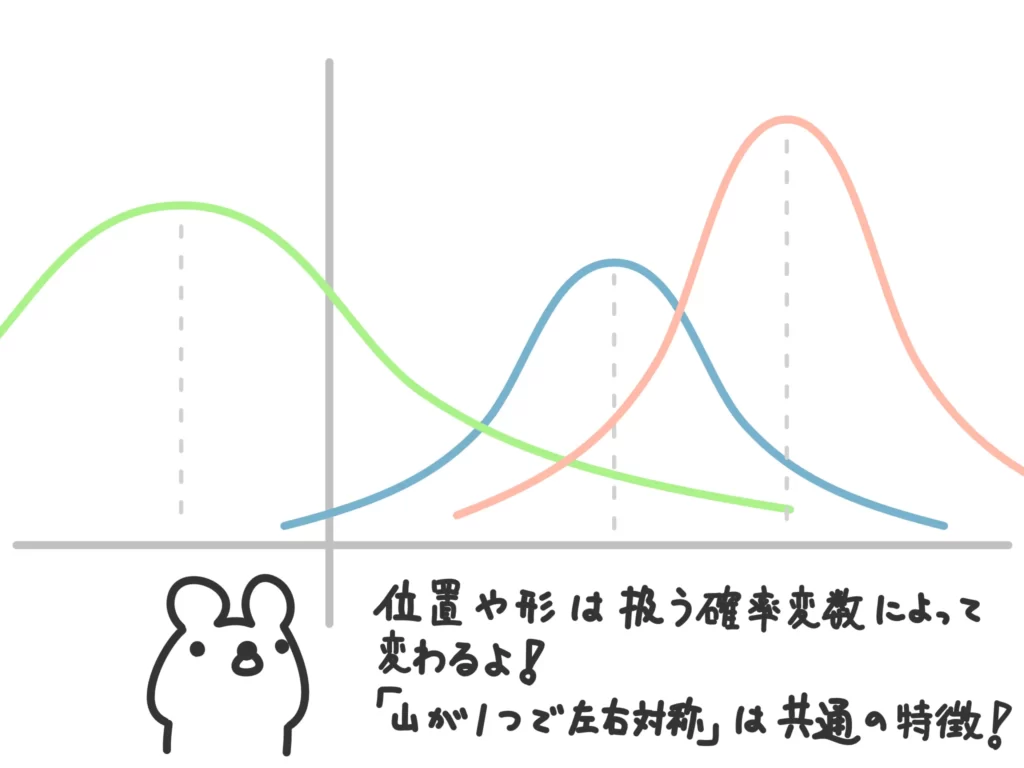
「山が一つで左右対称。」

これが正規分布の特徴です。

正規分布は「山が一つで左右対称」という特徴を持ちますが、この特徴を維持しつつ、２つの要素によって位置と形が変わります。

その二つの要素は平均と分散です。

確率変数\(X\)が、平均\(m\)、分散\(\sigma ^2\)の正規分布に従うとき、「正規分布\(N(m, \sigma ^2)\)に従う」と書きます。

言いたいことはわかります。ですが、安心してください。この確率密度関数を覚える必要はありません。

あくまでこういう確率密度関数になるよという紹介で、これを使って何か問題を解く、ということはありません。

ここで覚えておかないといけないことは、

• 確率変数\(X\)が、平均\(m\)、分散\(\sigma ^2\)の正規分布に従うとき、「正規分布\(N(m, \sigma ^2)\)に従う」と書く。
• 形は釣鐘型で平均\(m\)と分散\(\sigma ^2\)の値によって、位置と形が変わる。

という点です。

正規分布と標準正規分布

「色々な現象が正規分布に従う」という話をしましたが、正規分布はキレイな釣鐘型をしている、というだけで形は様々です。

例えば、

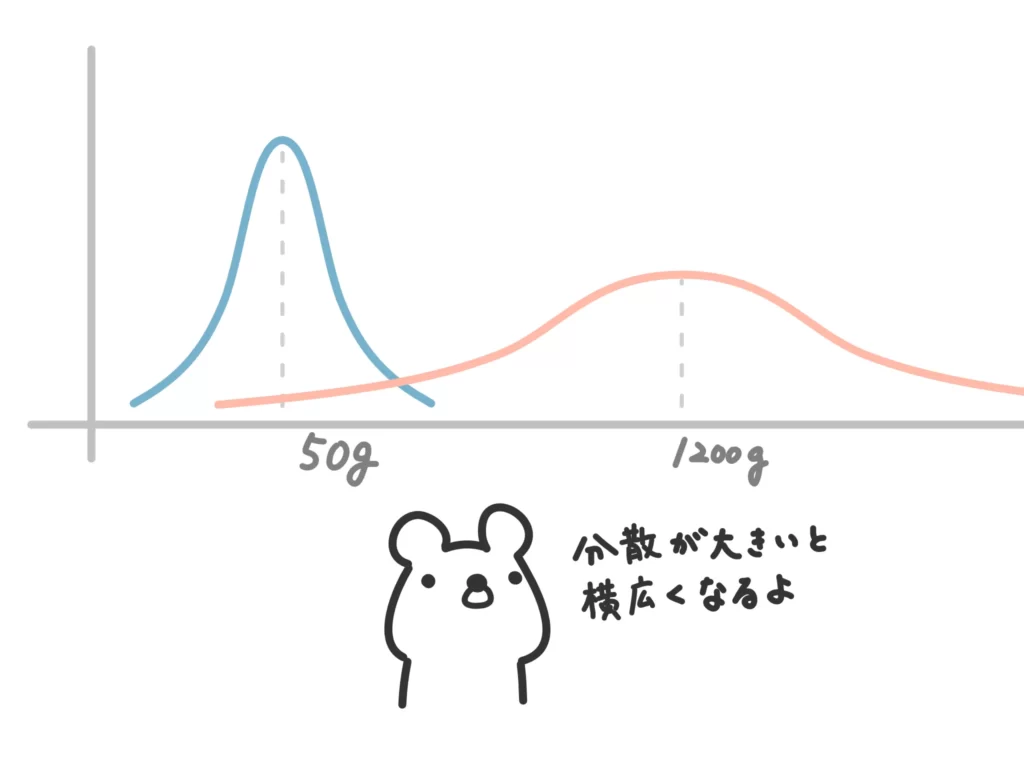
こんな感じで、形は様々です。ただ、ここで

と聞かれたら、いくらキレイな釣鐘型とはいえ、直接計算することは難しいです。

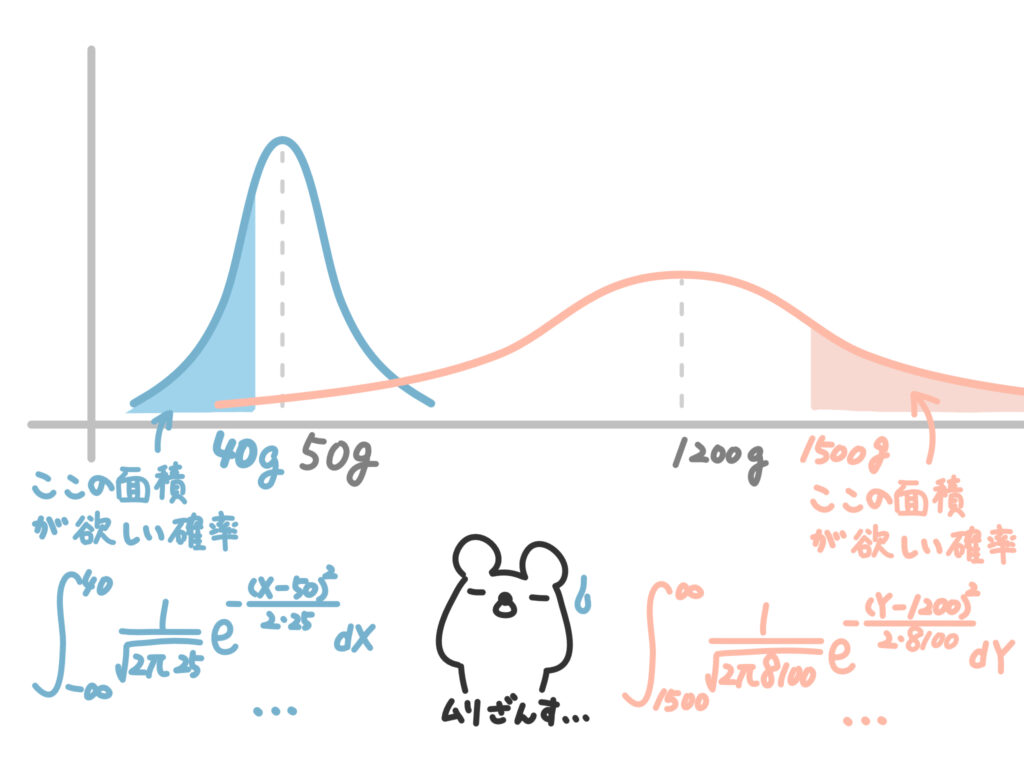
じゃあどうするか？というと、正規分布を標準正規分布に変換して確率を求めます。

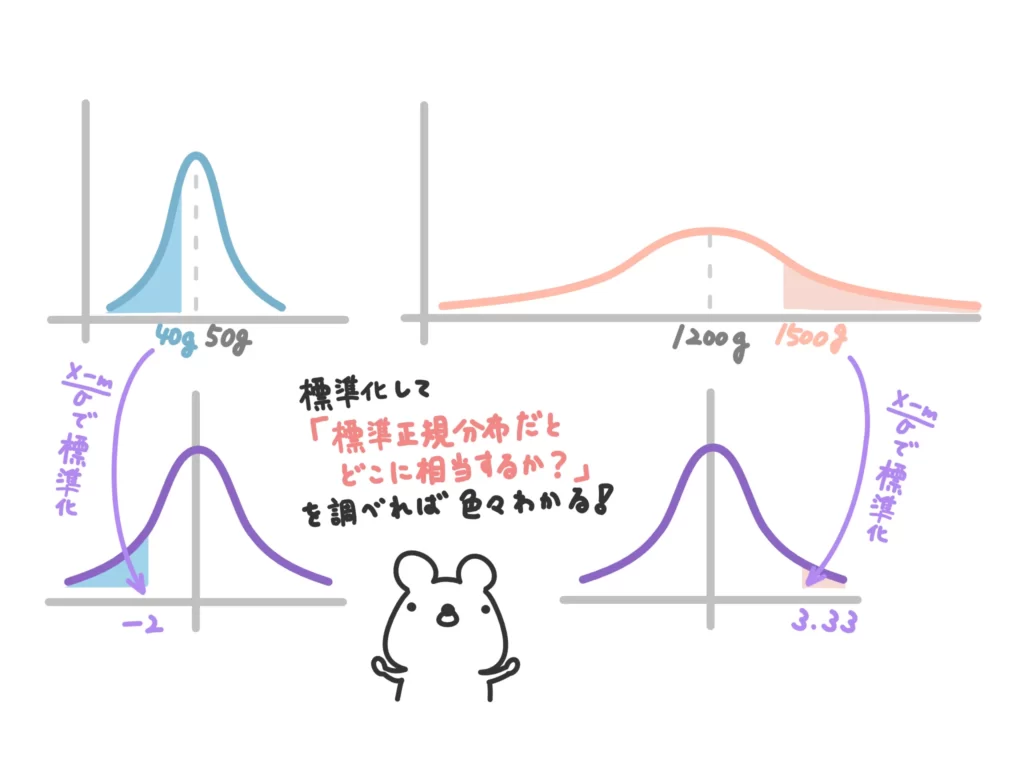
ですので、「正規分布」→「標準正規分布に変換（標準化）」→「標準正規分布上で欲しい確率や検定を行う」という流れで正規分布を処理していきます。

二項分布と正規分布の関係

実は二項分布は正規分布と深い関係にあります！

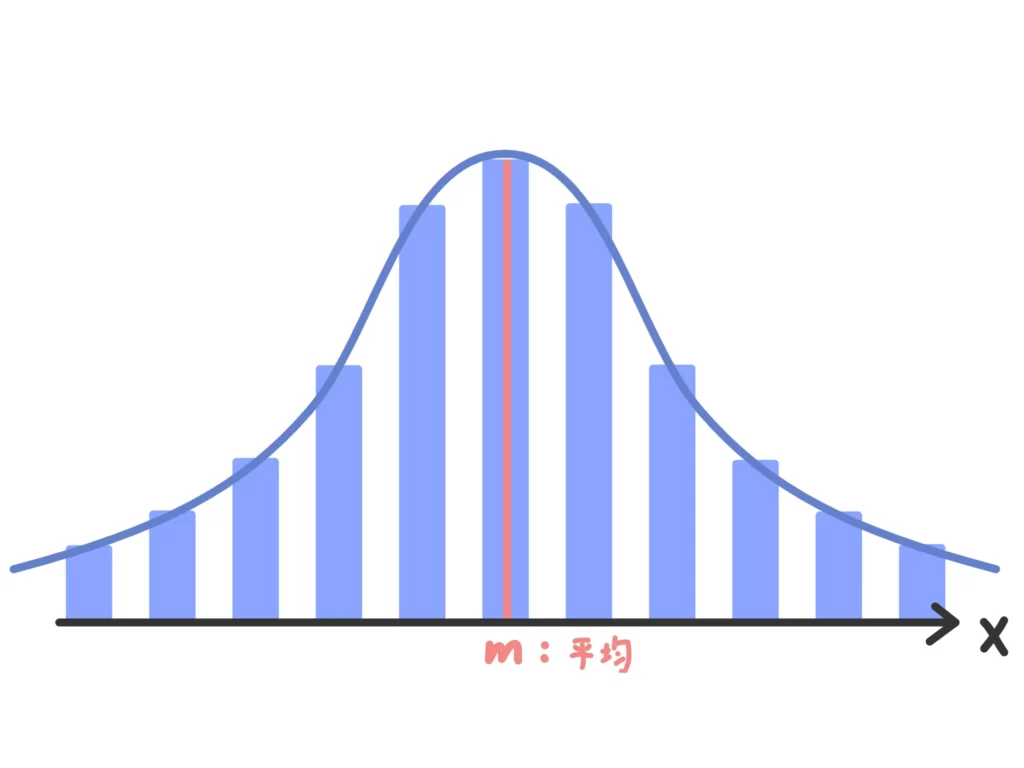
二項分布は離散型ですが、

「中央に山がある」「山を軸に左右対称」である、と正規分布に似た性質を持ちます。

そして、実際に二項分布の試行回数が多ければ、二項分布は正規分布で近似できる、という性質があります。

ですので、二項分布についても、「二項分布」→「正規分布に近似」→「標準正規分布に変換（標準化）して解析」の流れで確率を求めたり、推定や検定を行ったりします。

まとめ

正規分布についての説明でした。

正規分布は重要ですが、「そういうものがある」というのと「実際の計算は標準正規分布に標準化して行う」という点を押さえておけばOKです。

あと、「平均と分散で形が決まるから\(N(m,\sigma ^2)\)と書くんだな」という表現の仕方は覚えておいてください。