重積分のやり方を基本から丁寧に！積分範囲や重積分のイメージも図解！

2023年4月1日2023年9月17日

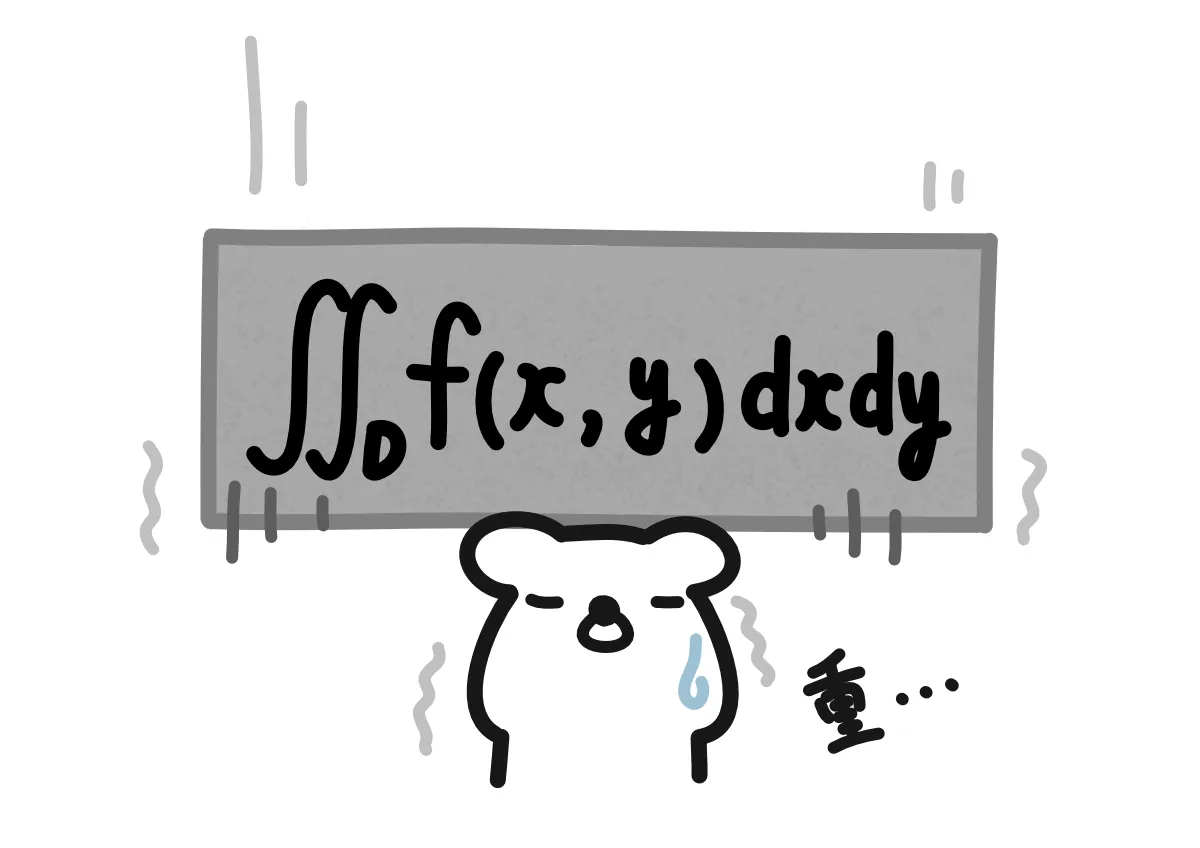
重積分は2変数関数の積分方法です。

大学で学ぶ範囲ですが、イメージを捉えるだけだったらそんなに難しくありません。高校の積分がわかっていれば理解できると思います。

この記事では重積分の基本について解説していきます。

このブログで活躍してるクマのLINEスタンプもあります！

重積分とは？

まず断っておきますが、この記事では、高校で習う１変数の積分を２変数に拡張した「２重積分」の説明をしていきます。ですので、この記事内では「重積分」は「２重積分」のことだと思ってください。

せんせ

ま、実際に２重積分のことを「重積分」と呼んだりもします。
これ以降３変数、４変数、…と続いても、イメージはしにくくなりますが、考え方は一緒ですね。

それでは、重積分の基本についてサクッと理解していきましょう！

２変数関数

重積分は２変数の関数を積分するので、２変数関数\(z = f(x, y)\)という関数が必要になります。

この\(z = f(x, y)\)は\(xyz\)空間上の平面を表す関数だと思っておいてください。

せんせ

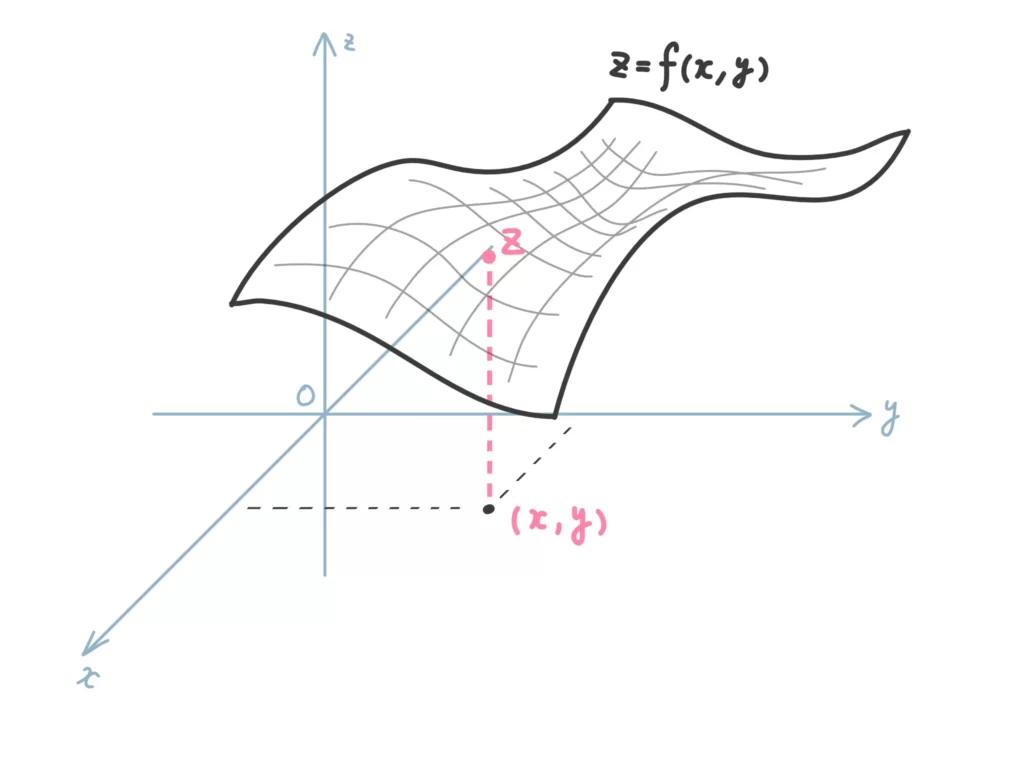
\((x,y)\)という\(xy\)平面上の点によって\(z\)（高さ）がただ一つ決まる、と思えば、それの集まりは\(xyz\)空間上の平面になりますよね。

重積分の範囲とイメージ

この\(xyz\)空間上の平面について、ある領域\(D\)に対して積分計算をしていくことを重積分といいます。

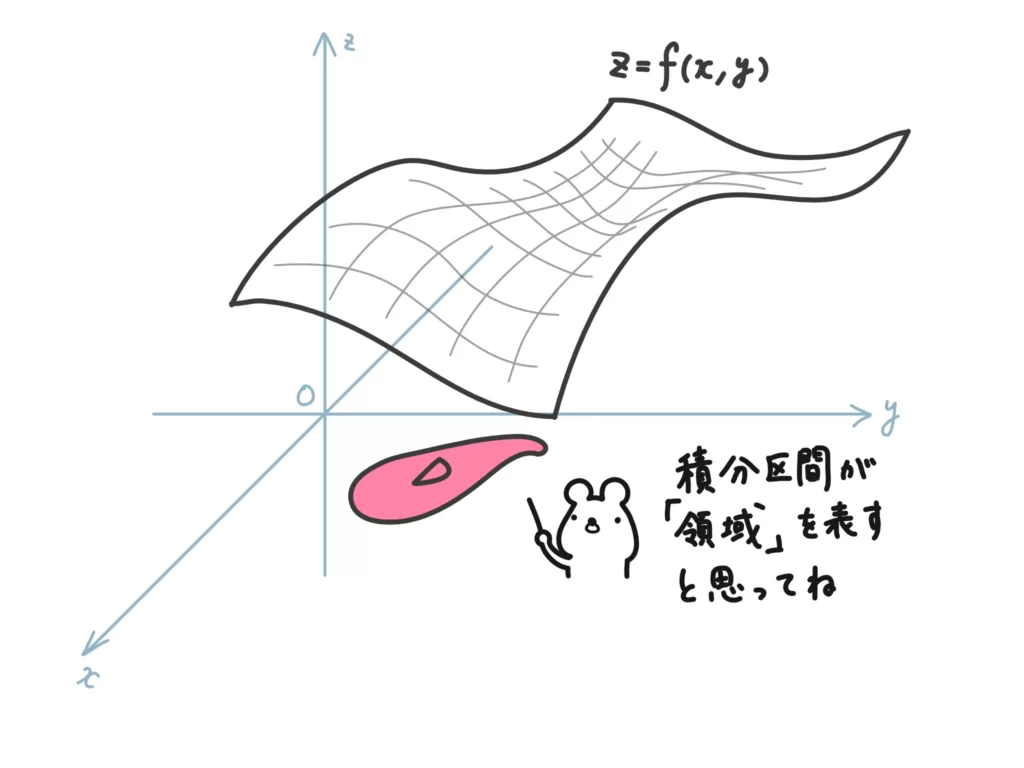
重積分は\(x\)、\(y\)について順次、積分をしていくのですが、この　\(x\)と\(y\)の範囲が領域\(D\)になる、ということですね。

せんせ

積分ですから「\(x\)と\(y\)の範囲」があります。この「\(x\)と\(y\)の範囲」が\(xyz\)空間で言うと「領域」になるということですね。

この領域と\(z = f(x, y)\)に囲まれた空間の体積を求める計算が重積分になります。

せんせ

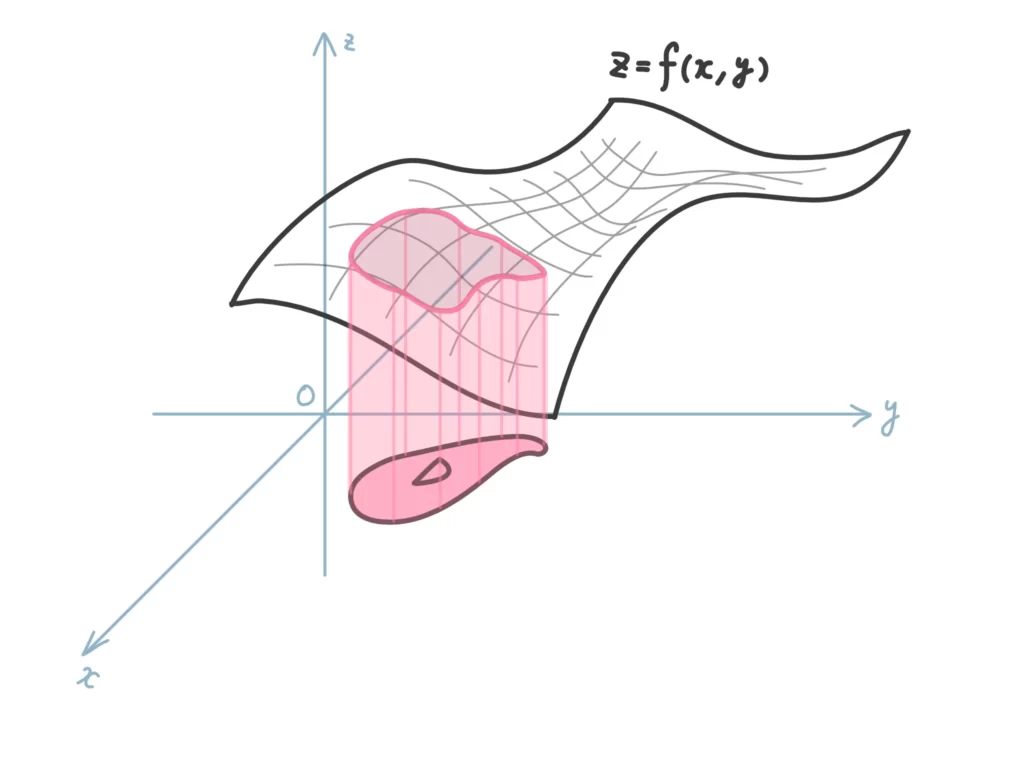
「体積」はイメージの話です。１変数の定積分が、計算上負の値になることもあるように、２変数の重積分が計算上負の値になることもあります。

感覚としては、１変数の定積分（平面）のときに細ーい短冊の和で面積を計算したのを、２変数（空間）に拡張した感じですね。

重積分の表現方法と計算方法

ここまでは重積分の「イメージ」の話でしたが、ここからは表現方法と計算方法です。

せんせ

ただ、こちらは全然難しくないです！

重積分

\(xy\)平面上の領域\(D\)において、\(z = f(x, y)\)に対する重積分を

\(\displaystyle \int\!\!\!\int_D f(x,y)dxdy\)

と書く。\(dxdy\)は面積要素ということもある。

重積分の計算については、累次積分（るいじせきぶん）といって、簡単に言うと「順番に積分（着目している文字以外は定数とみなす）」していきます。

例題．領域\(D=\{ (x,y)|0 \leq x \leq 1, 0 \leq y \leq x \} \)における\(f(x,y)=x+y\)の重積分を求めよ。

方法としては、

(i) \(y\)を積分（\(x\)固定）→\(x\)を積分

(ii) \(x\)を積分（\(y\)固定）→\(y\)を積分

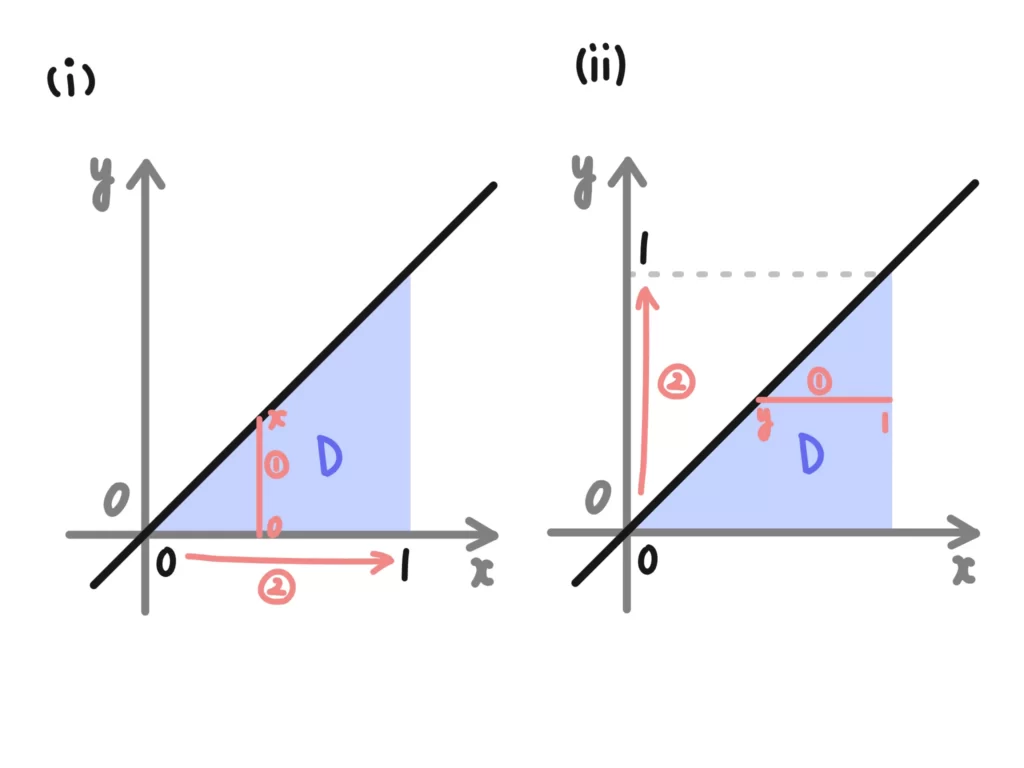
の２パターンあります。

（iの解）

求める重積分\(V\)は

\(\displaystyle V=\int\!\!\!\int _D f(x,y)dxdy\)

\(\displaystyle \quad = \int_0^1 \left\{ \int_0^x(x+y)dy \right\} dx\)

\(\displaystyle \quad = \int_0^1 \left[ xy + \frac{1}{2}y^2 \right]_0^x dx\)

\(\displaystyle \quad = \int_0^1 \left( x \cdot x + \frac{1}{2}x^2 \right) dx\)

\(\displaystyle \quad = \int_0^1 \frac{3}{2}x^2dx\)

\(\displaystyle \quad = \left[ \frac{1}{2}x^3 \right]_0^1 = \frac{1}{2}\)…（答）

（iiの解）

\(0 \leq x \leq 1, 0 \leq y \leq x \)より、\(0 \leq y \leq 1, y \leq x \leq 1\)なので、

求める重積分\(V\)は

\(\displaystyle V=\int\!\!\!\int _D f(x,y)dxdy\)

\(\displaystyle \quad = \int_0^1 \left\{ \int_y^1(x+y)dx \right\} dy\)

\(\displaystyle \quad = \int_0^1 \left[ \frac{1}{2}x^2 + yx \right]_y^1 dy\)

\(\displaystyle \quad = \int_0^1 \left\{ \frac{1}{2} + y – \left( \frac{1}{2}y^2 + y^2 \right) \right\} dy\)

\(\displaystyle \quad = \int_0^1 \left( -\frac{3}{2}x^2 + y + \frac{1}{2} \right) dy\)

\(\displaystyle \quad = \left[ -\frac{1}{2}x^3 + \frac{1}{2}y^2 + \frac{1}{2}y \right]_0^1 = \frac{1}{2}\)…（答）

せんせ

当たり前ですが、どちらも答えは同じですね。

重積分の性質

基本的に１変数の積分のような性質です。

\(\displaystyle \int\!\!\!\int_D \{ kf(x,y) \pm l g(x, y)\}dxdy\)\(\displaystyle \quad = k \int\!\!\!\int_D f(x,y)dxdy \pm l \int\!\!\!\int_Dg(x, y)dxdy\)
領域\(D\)を\(D_1\)、\(D_2\)に分割する場合、

\(\displaystyle \int\!\!\!\int_D f(x,y)dxdy=\) \(\displaystyle \int\!\!\!\int_{D_1} f(x,y)dxdy+\int\!\!\!\int_{D_2} f(x,y)dxdy\)

のように計算できます。１変数のときに積分区間を分けるのと同じ要領ですね。

また、\(D\)が長方形領域（\(x\)、\(y\)の積分区間がそれぞれ定数\(a \leq x \leq b\)、\(c \leq y \leq d\)）で、\(f(x,y)\)が\(x\)のみの関数\(g(x)\)と\(y\)のみの関数\(h(y)\)の積\(f(x,y)=g(x)h(y)\)に分けられるとき、

\(\displaystyle \int\!\!\!\int_D g(x)h(y)dxdy= \int_a^b g(x)dx \int_c^d h(y) dy \)

のように、\(x\)、\(y\)それぞれの積分の積に分解できます。

せんせ

最後の性質は２変数ならでは、ですね。ガウス積分を求めるときに使ったりします。

勉強が終わったらちょっと一息…Youtubeもやってます！バイクで走りながら大分を楽しく紹介中！ぜひご覧ください。