ヤコビアンによる重積分の変数変換を図と例題でわかりやすく！

重積分の変数変換（置換）について説明しますが、まずは１変数の積分の変数変換について押さえておくと理解しやすいと思います。

この記事の\(g'(t)\)の意味のところですね。ここの感覚がわかっていると、重積分の変数変換も理解しやすいです。

この記事では重積分の変数変換、特にヤコビアンについて詳しく説明していきます。

重積分の変数変換

ヤコビアンは行列\(\begin{pmatrix} \frac{\partial g}{\partial u} & \frac{\partial g}{\partial v} \\ \frac{\partial h}{\partial u} & \frac{\partial h}{\partial v} \end{pmatrix} \)の行列式に絶対値をつけたものです。ちなみに、この行列のことをヤコビ行列といいます。

という方はこちらの記事をご覧下さい。

行列式を理解しなくても、偏微分（\(\displaystyle \frac{\partial x}{\partial u}\)は「\(x=g(u,v)\)の\(v\)を定数として変数\(u\)で微分する。」の意味。他も同様。）の計算方法さえわかれば計算はできます。

ただ、行列と行列式の意味を押さえておいた方がヤコビアンのイメージが理解しやすいかな、と思います。

そもそも\(dxdy\)は面積要素と言われるもので、重積分は領域に関して積分する計算です。

その面積要素を補正するものがヤコビアンだと思ってください。

ここで、２変数関数\(z=f(x,y)\)の全微分は次のように計算されます。

\(\displaystyle dz = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy\)

つまり、今回の話では\(x = g(u, v) \)とおくと、その全微分は、

\(\displaystyle dx = \frac{\partial g}{\partial u} du + \frac{\partial g}{\partial v} dv \)…①

となります。\(y=h(u, v)\)についても同様に、

\(\displaystyle dy = \frac{\partial h}{\partial u} du + \frac{\partial h}{\partial v} dv \)…②

となります。

行列の積を使えば、①、②の式は

\(\begin{pmatrix} \frac{\partial g}{\partial u} & \frac{\partial g}{\partial v} \\ \frac{\partial h}{\partial u} & \frac{\partial h}{\partial v} \end{pmatrix} \begin{pmatrix} du \\ dv \end{pmatrix} =\begin{pmatrix} dx \\ dy \end{pmatrix} \)

とまとめることができます。ここで、こちらの記事でも説明していますが、行列は、ベクトルに掛けるとベクトル変換を表し、その行列式は拡大倍率を表します。

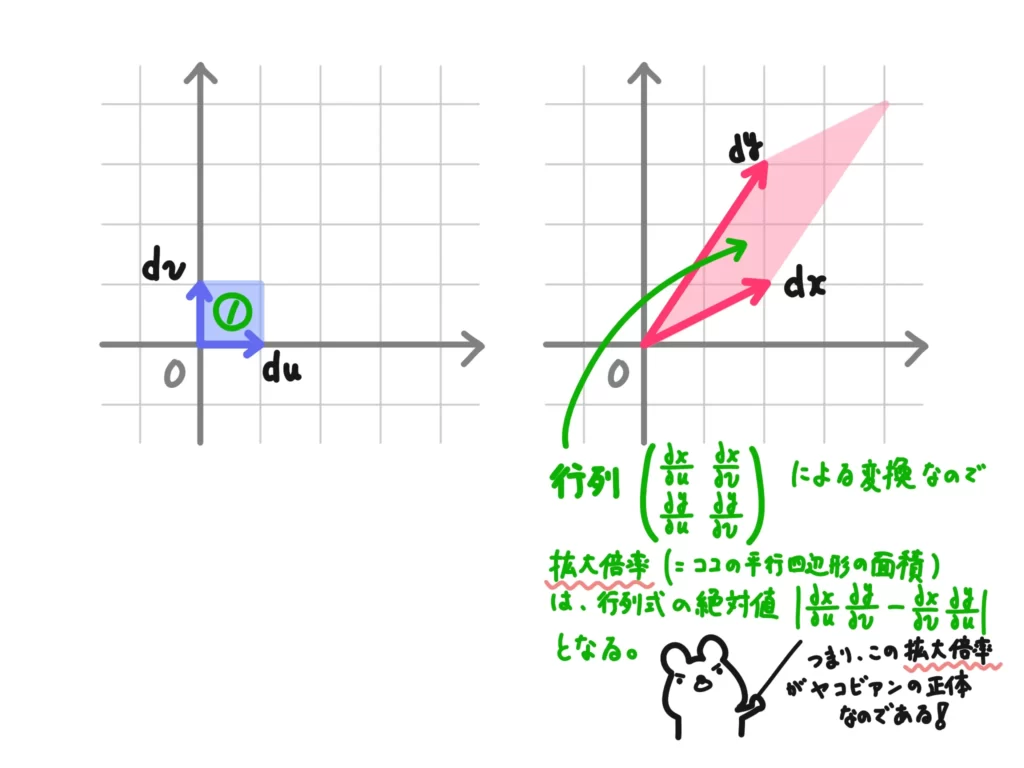
元の話は\(x\)、\(y\)を\(u\)、\(v\)に置き換えているので、この行列の計算では一見逆方向に変換しているように見えます。

ですが、今やりたいことは「\(dudv\)をどのように補正したら\(dxdy\)になるか？」ですので、この補正分のヤコビアンを掛けることで\(dxdy\)を\(dudv\)で上手く表現できることになります。

この、置換積分の補正の感覚については、こちらでも説明していますので、合わせて見ていただけると嬉しいです。

この記事の\(g'(t)\)の役割がヤコビアンなんですね。

ド定番！ヤコビアンで極座標に変換！

これはどこのサイトでも解説しているのですが、\(x\)、\(y\)を極座標（変数\(r\)、\(\theta\)）に変換してみます。

例．領域\(D=\{ x^2 + y^2 \leq 1 \} \)における\(f(x,y) = e^{-x^2-y^2}\)の重積分を求めよ。

この関数、「\(-x^2-y^2=-(x^2+y^2)\)」が見えるので、極座標で考えたくなります。

まずは変数を置き換えます。

極座標表示なので、\(x=r\cos{\theta}\)、\(y=r\sin{\theta}\)と置きます。

ここで、\(x\)、\(y\)をそれぞれ\(r\)、\(\theta\)で偏微分すると、

\(\displaystyle \frac{\partial x}{\partial r} = \cos{\theta}\)

\(\displaystyle \frac{\partial x}{\partial \theta} = -r\sin{\theta}\)

\(\displaystyle \frac{\partial y}{\partial r} = \sin{\theta}\)

\(\displaystyle \frac{\partial y}{\partial \theta} = r\cos{\theta}\)

となります。なので、ヤコビ行列\(J\)とヤコビアン\(||J||\)は、それぞれ

\( J = \begin{pmatrix} \cos{\theta} & -r\sin{\theta} \\ \sin{\theta} & r\cos{\theta} \end{pmatrix}\)

\(||J|| = | \cos{\theta}\cdot r\cos{\theta} – ( -r\sin{\theta})\cdot \sin{\theta}| = |r(\cos^2{\theta}+\sin^2{\theta})|\)

\( \quad = r\)

となります。ちなみに、極座標における\(r\)は、普通は一意性を保つために\(r \geq 0\)で定義します（\(r<0\)まで認めちゃうと、各点(\(x\),\(y\))をいろんなパターンで表せてしまいます。同様に\(\theta\)についても普通は\(0 \leq \theta < 2\pi\)で定義します）。

つまり、極座標変換をしたときのヤコビアンは\(||J|| = r\)となります。

まとめ

重積分の変数変換の解説でした。

ヤコビアン、という行列式まで持ち出して変数変換をしないといけないのは大変ですが、その意味がわかってくると、色々な知識と結びついてくるので面白いです。

ぜひ、一つずつじっくりと勉強してみてください。