“役に立つ”行列の基本と考え方のコツをわかりやすく説明

2023年3月21日2023年9月22日

「行列」…今の高校の教育課程では習いませんが、大学の「線形代数」という分野で出てきます。

実は、行列はAIで必須の学習分野で、今ちょっとしたブームになっています。

ちなみに、昔は高校で行列を習っていた時期もありました。正直「なんでこんなこと勉強するんじゃ！」と思っていましたが、後々ベクトルや解析と結びつくので、考え方を理解していると応用範囲が広く、使いやすい武器です。

この記事では、「行列とは？」という説明から、行列の基本的な計算方法の解説をしていきます。

このブログで活躍してるクマのLINEスタンプもあります！

行列とは？

行列とは「数の組を行と列に並べて表現したもの」です。

せんせ

言葉で説明してもわかりにくいですね…。百聞は一見にしかず。とりあえず次の行列の表し方を見てください！

\(A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\)

こんな感じですね。数字（or当然文字でもOK）を縦と横に書き並べて、それを一組として扱います。

また、行列は\(A\)などアルファベットの大文字で表し、それぞれの数字（or文字）の間はスペースをとって区切りを表現します。カンマなどで区切ることはしません。

せんせ

ではまず、基本的な行列の用語から押さえていきましょう！

行列の形

先ほど、

\(A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\)

という行列の例をあげましたが、行列のサイズは２×２とは限りません。

\(B = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}\)

こんな形もアリです。

行列がどんなサイズか？を、「\(m \times n\)行列」または「\(m\)行\(n\)列の行列」と言って表します。横方向が行、縦方向が列です。

せんせ

ですので、上記の例の\(A\)は「\(2 \times 2\)行列」、\(B\)は「\(2 \times 3\)行列」といいます。

私はなんとなく「行」→「横書きの教科書とかの１行目などのイメージ」、「列」→「教室の席の縦列のイメージ」ですね。教員生活が長かったので…。

せんせ

まぁ、なんでもいいので覚えてくれればOKです笑

ちなみに、\(m \times m\)行列（行と列の数が同じ）を\(m\)次正方行列といいます。

せんせ

行と列の数が同じだったら行列が正方形になりますよね。先ほどの\(A\)は「２次正方行列」です。

行列の成分

行列の、\(i\)行\(j\)列の値を\((i,j)\)成分、といい、\(a_{ij}\)と表します。

\( \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}\)

具体的に書くとこんな感じですね。

行列の基本的な計算

まだまだ基本的な用語が出てくるのですが、先に行列の計算について話をしておきます。

足し算・引き算

行列の足し算・引き算は簡単です。

結論から言うと「同じ成分を足したり引いたりする」だけ。ですので、サイズが同じ行列同士でないと足し算・引き算はできません。

例．\(A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\)、\(B = \begin{pmatrix} 3 & 4 \\ 2 & 1 \end{pmatrix}\)とすると、

\(A + B = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} + \begin{pmatrix} 3 & 4 \\ 2 & 1 \end{pmatrix}\)

\(\quad = \begin{pmatrix} 1+3 & 2+4 \\ 3+2 & 4+1 \end{pmatrix} = \begin{pmatrix} 4 & 6 \\ 5 & 5 \end{pmatrix}\)

引き算も同じ要領ですね。

\(A – B = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} – \begin{pmatrix} 3 & 4 \\ 2 & 1 \end{pmatrix}\)

\(\quad = \begin{pmatrix} 1-3 & 2-4 \\ 3-2 & 4-1 \end{pmatrix} = \begin{pmatrix} -2 & -2 \\ 1 & 3 \end{pmatrix}\)

実数倍（スカラー倍）

実数倍（スカラー倍）は、それぞれの成分をその実数倍します。

例．\(A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\)とすると、

\(2A = \begin{pmatrix} 2 \times 1 & 2 \times 2 \\ 2 \times 3 & 2 \times 4 \end{pmatrix} = \begin{pmatrix} 2 & 4 \\ 6 & 8 \end{pmatrix}\)

ここまでは直感的で簡単ですね。

ちなみに、この「足し算・引き算」「実数倍」の計算は、カンのいい人なら「ベクトルに似てるな」と思えるはずです。

あとで説明しますが、実はベクトルも行列として表現することができます。逆に行列はベクトルを拡張したもの、と思っておいてください。

そうすると、次の「掛け算」も理解しやすいはずです。

掛け算

ということで、掛け算ですが、これは足し算や引き算のように「同じ成分を掛け算する…わけではない」です！

先ほど「ベクトルも行列として表現することができる」とちょっとだけ言いましたが、「ベクトルの内積」を成分同士の掛け算で計算しないように、行列でも積の計算のときに単純に成分同士を掛け合わせることはしません！

この掛け算（積）が行列の特徴的な演算になります。

せんせ

では、具体的にどのように行列の積を計算するか、見てみましょう！

\(A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\)、\(B = \begin{pmatrix} p & q \\ r & s \end{pmatrix}\)とすると、行列の積\(AB\)は

\(AB = \begin{pmatrix} ap+br & aq+bs \\ cp+dr & cq+ds \end{pmatrix}\)

と計算します。

たろぅ

（なんのこっちゃ…）

という声が聞こえてきそうですが、よくみると、積\(AB\)のそれぞれの成分は、ベクトルの内積のような形（成分を掛けて足す）になっていることがわかります。

文字だとわかりにくいので、具体的な数字で表して、計算方法のコツを図にしておきます。

せんせ

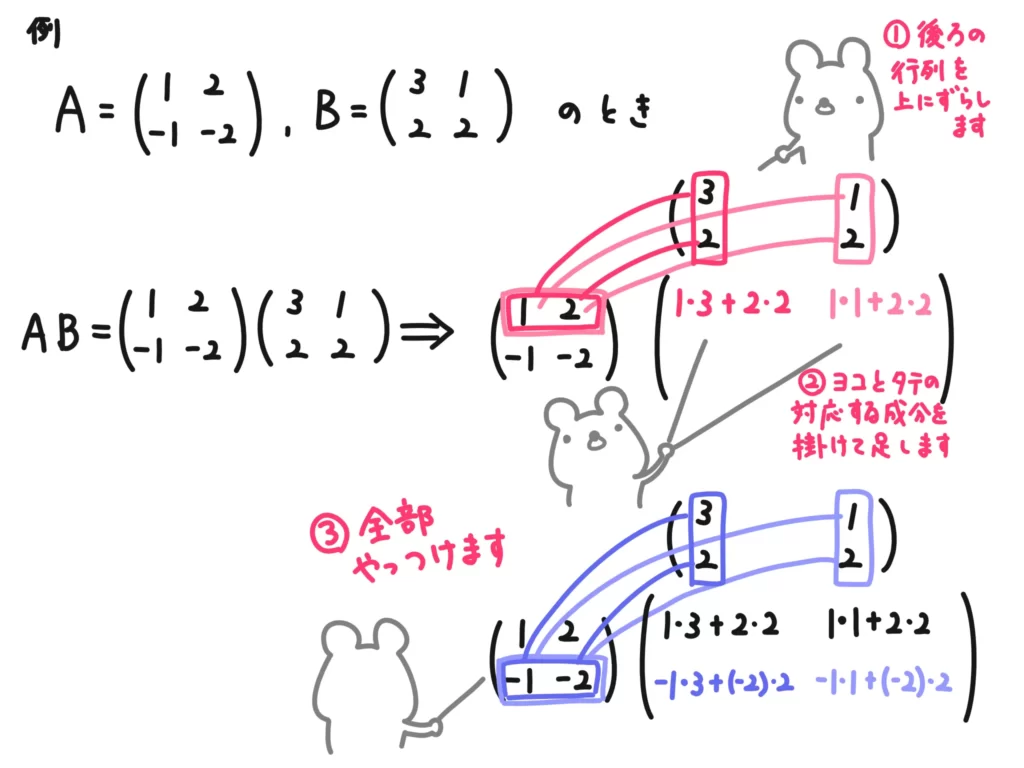
どんなサイズの行列でも積の計算ができるとは限りません。まぁ、やってみて計算できるやつはできるし、計算できないものは物理的に計算できません。

例．\( P = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\)、\( Q = \begin{pmatrix} 3 \\ 4 \end{pmatrix}\)という行列があったとします。\(Q\)もこんな形ですが、\(2\times 1\)行列という立派な行列です。

この行列について、積\(PQ\)は

\(PQ = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \begin{pmatrix} 3 \\ 4 \end{pmatrix} = \begin{pmatrix} 1 \times 3 + 2 \times 4 \\ 3 \times 3 + 4 \times 4 \end{pmatrix} = \begin{pmatrix} 11 \\ 25 \end{pmatrix} \)

と計算できますが、積\(QP\)は

\(QP =\begin{pmatrix} 3 \\ 4 \end{pmatrix} \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} = \cdots ?\)

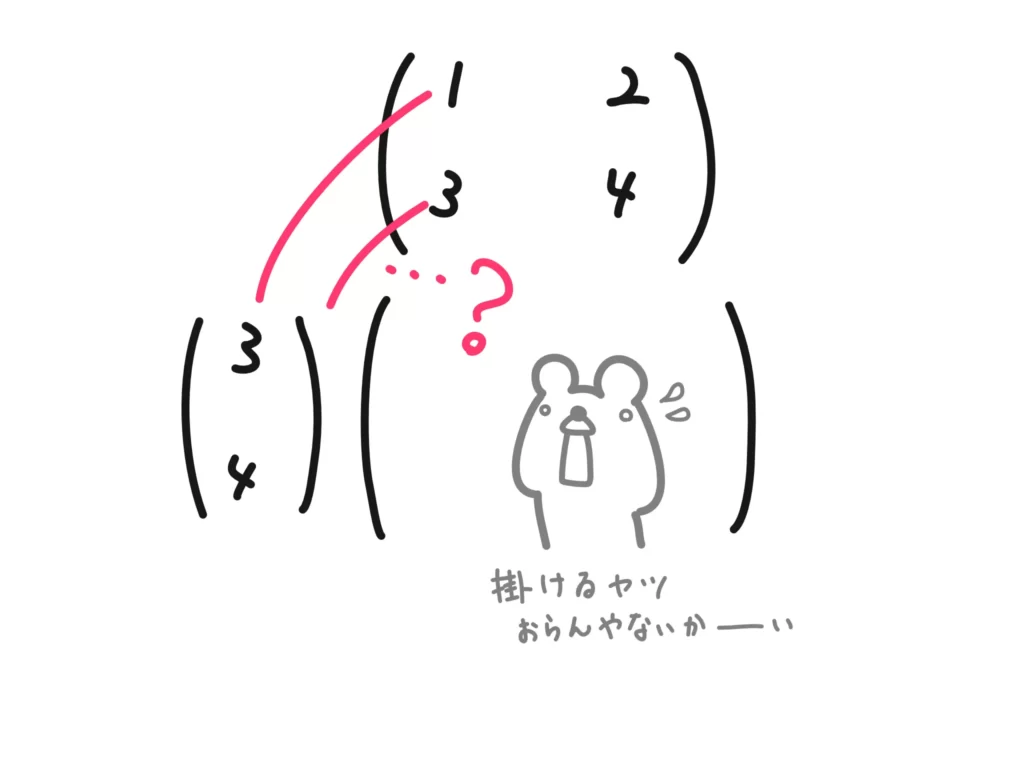
となり、計算できないことがわかります。

せんせ

このように、行列の積は\(PQ\)と\(QP\)で、計算できるかできないかが変わってきます。

また、次のように、積の順番を交換したときに、例え計算できたとしても同じ結果になるとは限りません。

例．\( R = \begin{pmatrix} 1 & 2 \\ 1 & 2 \end{pmatrix}\)、\( S = \begin{pmatrix} -1 & -2 \\ 1 & 2 \end{pmatrix}\)という行列があったとします。

これらの積\(RS\)と\(SR\)はそれぞれ次のようになります。

\(RS = \begin{pmatrix} 1 & 2 \\ 1 & 2 \end{pmatrix}\begin{pmatrix} -1 & -2 \\ 1 & 2 \end{pmatrix}\)

\( \quad = \begin{pmatrix} -1+2 & -2+4 \\ -1+2 & -2+4 \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 1 & 2 \end{pmatrix}\)

\(SR = \begin{pmatrix} -1 & -2 \\ 1 & 2 \end{pmatrix}\begin{pmatrix} 1 & 2 \\ 1 & 2 \end{pmatrix}\)

\( \quad = \begin{pmatrix} -1-2 & -2-4 \\ 1+2 & 2+4 \end{pmatrix} = \begin{pmatrix} -3 & -6 \\ 3 & 6 \end{pmatrix}\)

\(RS \neq SR\)

積\(RS\)と\(SR\)は結果が全然違います。つまり、一般的に行列の積は交換法則が成り立ちません。

せんせ

積の交換法則が成り立たない…というのは高校までの他の分野ではないですよね。この辺りが行列の特徴になります。

ということで、行列の積に関しては「左から掛ける」「右から掛ける」をしっかりと区別します。

それらの積が計算できない可能性もあるし、できたとしても、左から掛けるのと右から掛けるのでは一般的に計算結果が違う、というのは重要な特徴なので押さえておいてください。

零行列と単位行列

せんせ

ここは「こういうものがあるよ」という話です。零行列と単位行列は普通の数（スカラー）の0と1に相当します。

零行列

すべての成分が0である行列を零行列といい、\(O\)と書きます。

例．\(O = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}\)

せんせ

２次正方行列ですが、こんな感じですべての成分が0である行列のことですね。

行列\(A\)と零行列\(O\)に関して、\(AO = OA =O\)となることはすぐにわかるはずです。

そしてもう一つ、実は零行列に関して面白い性質があります。

せんせ

とりあえず、次の行列の積を計算してみてください。

例．\( A = \begin{pmatrix} 1 & 2 \\ 2 & 4 \end{pmatrix}\)、\( B = \begin{pmatrix} -2 & 2 \\ 1 & -1 \end{pmatrix}\)の積\(AB\)

（解答）

\( AB = \begin{pmatrix} 1 & 2 \\ 2 & 4 \end{pmatrix}\begin{pmatrix} -2 & 2 \\ 1 & -1 \end{pmatrix}=\begin{pmatrix} -2+2 & 2-2 \\ -4+4 & 4-4 \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}=O\)

この例でわかるように、\(A \neq O\)、\(B \neq O\)でも、その積\(AB\)は\(AB=O\)になることがあります！

せんせ

これも普通の数ではありえない、行列の特徴ですね！このように、今までの数で常識的だったことが行列になると通用しない、ということが行列の面白いところです。

ちなみに、今の\(A\)、\(B\)の積\(BA\)（左右ひっくり返した）は

\( BA = \begin{pmatrix} -2 & 2 \\ 1 & -1 \end{pmatrix}\begin{pmatrix} 1 & 2 \\ 2 & 4 \end{pmatrix}=\cdots=\begin{pmatrix} 2 & 4 \\ -1 & -2 \end{pmatrix}\)

となり、零行列とはなりません。

せんせ

不思議ですねぇ。

単位行列

正方行列の左上から右下の成分のことを対角成分、といいます。

例1．\( \begin{pmatrix} \color{red}{a_{11}} & a_{12} \\ a_{21} & \color{red}{a_{22}} \end{pmatrix}\)

２次正方行列であれば、この\(a_{11}\)、\(a_{22}\)のことです。

この対角成分以外の成分が0である行列を対角行列、といいます。

例2．\( \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}\)

例3．\( \begin{pmatrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & -1 \end{pmatrix}\)

この対角行列同士は、積の計算がとても簡単にできます。

例えば、

\( \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}=\begin{pmatrix} 2 \cdot (-1) & 0 \\ 0 & 3 \cdot 1 \end{pmatrix} = \begin{pmatrix} -2 & 0 \\ 0 & 3 \end{pmatrix}\)

実際に計算してくれればわかりますが、こんな感じで対角成分だけ掛ければOKです。

そして、この対角成分がすべて1である対角行列を単位行列といって、\(E\)と書きます。

例4．\(E= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\)

例5．\( E=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}\)

これらはどちらも（２次、３次の）単位行列です。

単位行列を掛けてもその行列は変わらない、という性質があります。しかも、左から掛けても右から掛けても結果は同じです。

せんせ

なので、単位行列は普通の数の1にあたります。

例6．\(A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \)、２次の単位行列を\(E= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\)とすると、

\(EA =AE=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} =\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}=\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\)

おまけ「行列とベクトル」

ベクトルは「いくつかの成分を一組として扱う（２つの成分であれば平面ベクトル、３つの成分であれば空間ベクトル）」ので行列の一種とみることができます。

せんせ

行列でベクトルを表現する際は、縦の行列で表すことが多いです。

例1．\( \overrightarrow{a} = (1, 2)\)と成分表示で書くところを、\( \overrightarrow{a} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\)と書きます。

せんせ

縦書きにしていたら、成分計算もしやすいです！

例2．\( \overrightarrow{a} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\)、\( \overrightarrow{b} = \begin{pmatrix} -2 \\ 1 \end{pmatrix}\)のとき、

\(\overrightarrow{a}+2\overrightarrow{b} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}+2\begin{pmatrix} -2 \\ 1 \end{pmatrix}= \begin{pmatrix} -3 \\ 4 \end{pmatrix}\)

例3．片方を縦の行列ではなく横の行列にすれば、内積の計算も行列の積の計算で可能です。

\( \overrightarrow{a} = \begin{pmatrix} 1 & 2 \end{pmatrix}\)、\( \overrightarrow{b} = \begin{pmatrix} -2 \\ 1 \end{pmatrix}\)とすると、

\( \overrightarrow{a} \cdot \overrightarrow{b} = \begin{pmatrix} 1 & 2 \end{pmatrix}\begin{pmatrix} -2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \cdot (-2) + 2 \cdot 1 \end{pmatrix} = \begin{pmatrix} 0\end{pmatrix}\)

せんせ

まぁ、行列とみれば正確には\(1 \times 1\)行列になるんですけどね。でも、内積も行列の積で計算できるのは面白いですね。

まとめ

思った以上に長文になってしまいましたので、ポイントをまとめておきます。

行列とは、数の組を長方形状（もしくは正方形状）に並べて一組にしたもの。
行列の足し算・引き算、実数倍は成分同士の計算で行う。積は成分同士を掛けて足す、というちょっと特殊な計算になる。
行列の積は交換法則が基本的に成り立たない。また、\(A \neq O\)、\(B \neq O\)でも、その積\(AB\)が\(AB=O\)となることがある。
対角行列は後々出てくるので頭の片隅に置いておいてください。