PR
数列の基本!等比数列を基礎から徹底的に解説【公式の覚え方のイメージも】

数列の基本、等比数列…。
基本ではあるのですが、数列は公式が複雑になりがちです。
この記事では、等比数列の基本と公式のイメージを図を使いながら説明していきます。
等比数列とは?
 たろぅ
たろぅなんじゃ…このでかい紙は…。(嫌な予感がする…)



あ…たろう君。ちょうどいいところに来たわね。



イヤです!絶対にイヤです!



このA1サイズの紙5枚が生徒会室から出てきたんだけど、今度の文化祭企画で投票用紙が必要なんだよねぇ…。
で、このA1の紙を切ってA8サイズまで小さくしてね。
あと、A8まで切ったら枚数を数えておいてちょうだい。



あれ?ボクの「イヤです」のくだりは無視?そしてその作業は決定事項?
ということで等比数列です。
「A1」は紙のサイズですね。大きさは594mm×841mmです。
このA1を半分に切るとA2になります。
そしてA2の半分がA3、A3の半分がA4…と、半分のサイズに切る度にA○の◯の数字が増えていきます。



日頃よく目にする紙のサイズはA4ですね。
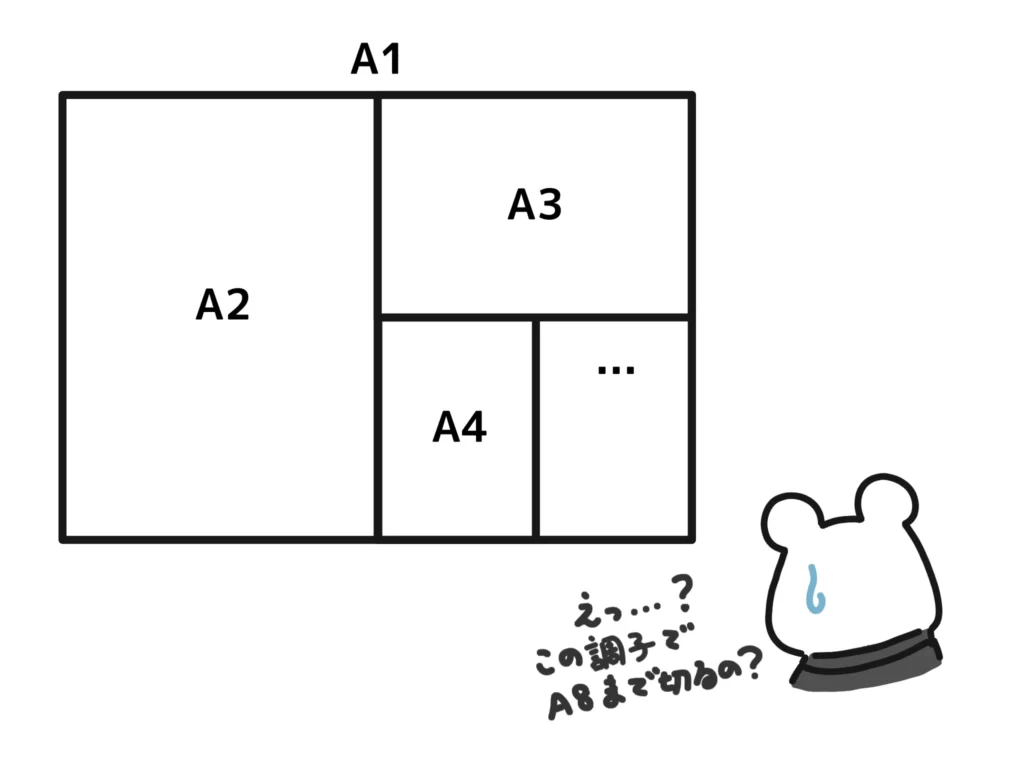

ちなみにA8のサイズは52mm×74mmです。かなり小さいですが、投票用紙くらいの使い道なら十分でしょう。
さて、このA1の紙5枚をA8サイズまで切ると何枚になるでしょうか?
まず、A2サイズに切ると、5枚の紙が10枚になります。そして、A3サイズに切ると、さらにその倍の20枚になりますよね?
この調子でA4→A5→…→A8まで切っていくと、枚数はどんどん倍になっていくのがわかります。
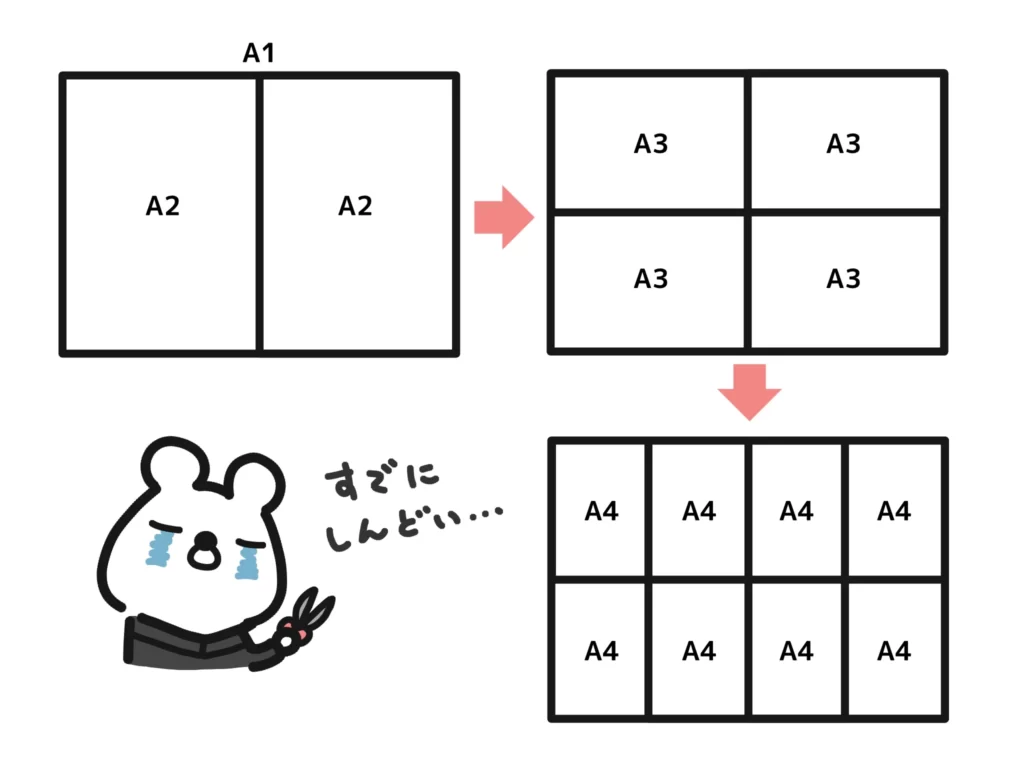

ということで、A8まで切ると枚数は次のように計算することができます。
\(5 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 =5 \times 2^7=640\)
A\(n\)サイズの枚数を\(a_n\)とすると、\(a_n\)は次のようになります。
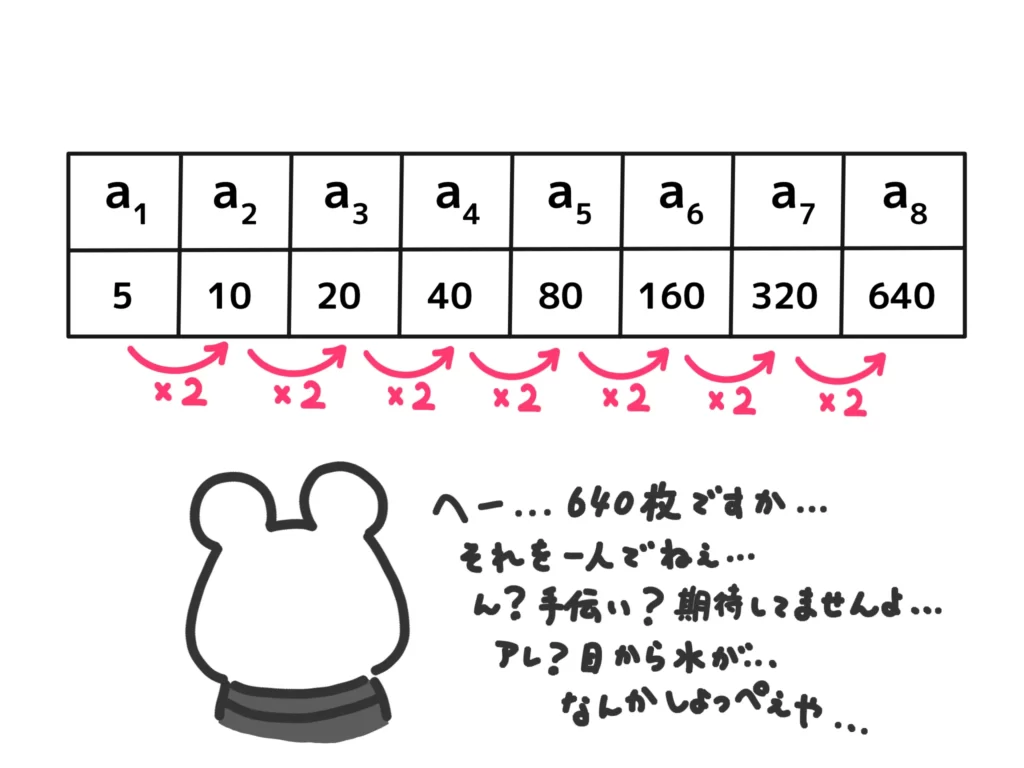

このように「前の項に、ある一定の数を掛けることで次の項が得られる」。このように作られる数列を等比数列、といいます。
等比数列を決定するのは、初項\(a\)と掛けていく「一定の数」\(r\)です。この「一定の数」のことを公比といいます。
等比数列の一般項の公式
等比数列の一般項(第\(n\)番目の項)は次のようになります。
等比数列の一般項
初項\(a\)、公比\(r\)の等比数列\( \{ a_n \} \)の一般項\(a_n\)は、
\(a_n = a \cdot r^{n-1}\)



公比\(r\)が\( (n-1) \)乗である、というところがポイントですね!
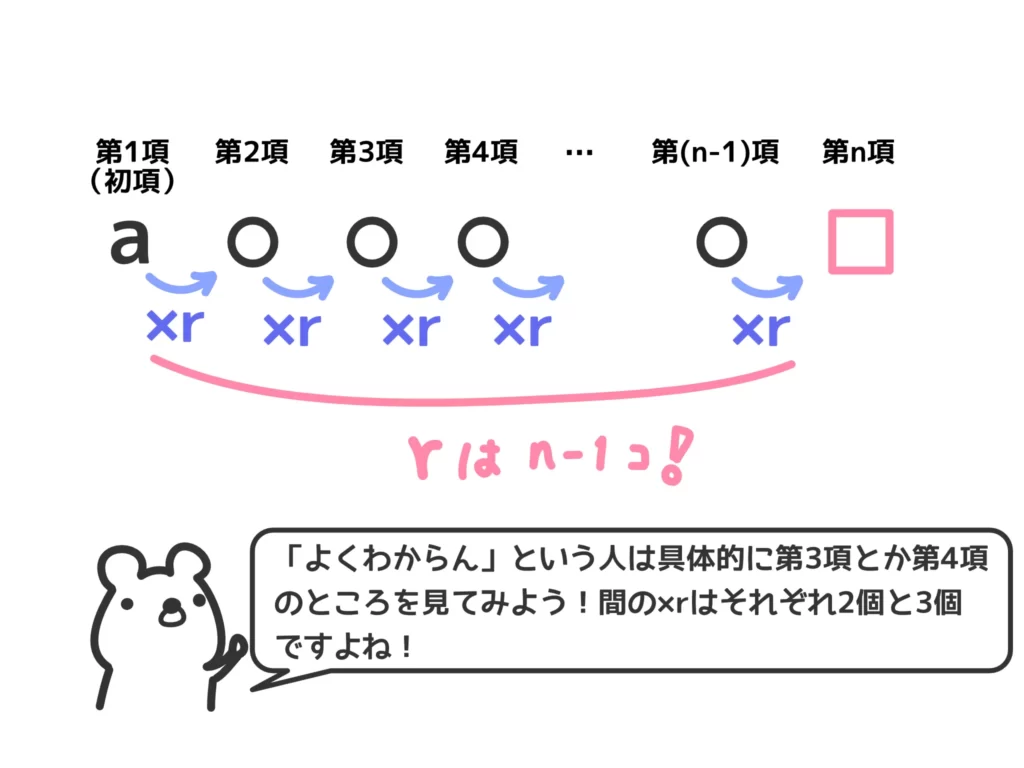

イメージは等差数列とほぼ一緒です。


計算方法が掛け算なので、一般項(第\(n\)番目の項)は\(a_n = a \times r \times r \times r \times \cdots \times r = a \cdot r^{n-1} \) となります。
等比数列の「等比」は「比が等しい」という意味です。
公比\(r\)の等比数列では、どんな自然数\(n\)に対しても、\(a_n\)と\(a_{n+1}\)の間には次のような関係が成り立っています。
\(a_{n+1} = a_n \cdot r\)
\(\displaystyle \frac{a_{n+1}}{a_n} = r\)



ということで、隣の項との比が常に等しい数列ということがわかります。
ちなみに、「この形のどこが比なんじゃい!」と思う人もいるかもしれません。
実は「分数は比を表す」という側面があります。



詳しくはこちらの記事をご覧ください。


ということで、この\(\displaystyle \frac{a_{n+1}}{a_n} = r\)は「比が等しい」という意味を表しています。
等比数列の和の公式
数列では、初項から第\(n\)項までの和もよく求めます。
等比数列の第\(n\)項までの和の公式は次のようになります。
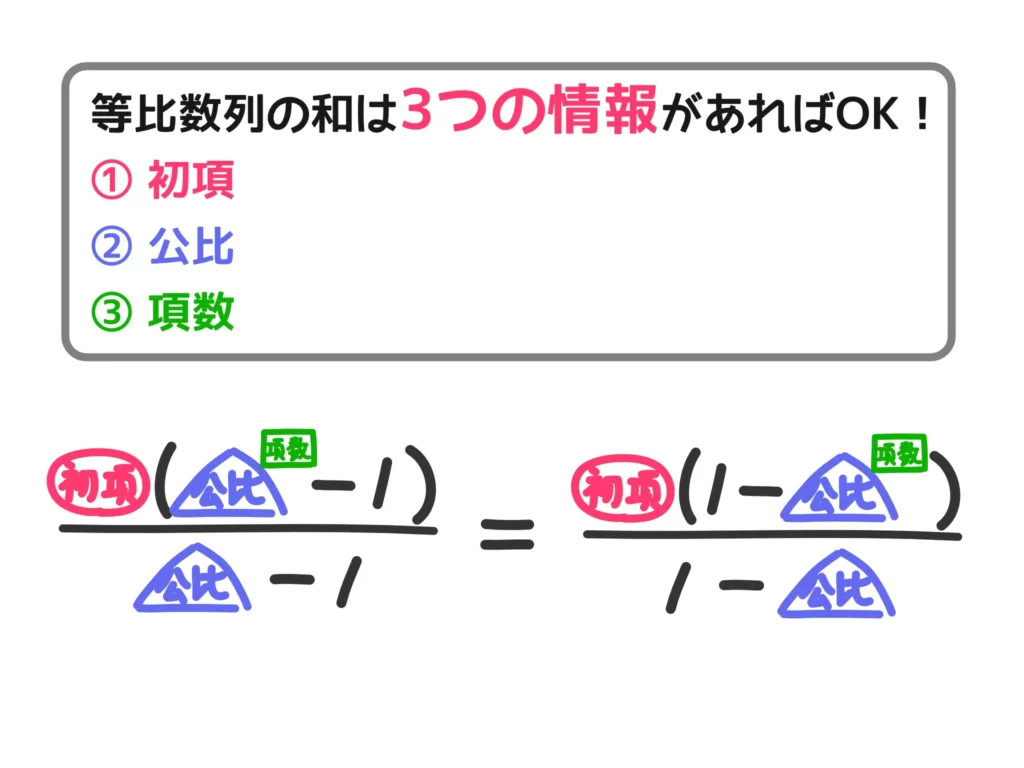
等比数列の和
初項\(a\)、公比\(r\)、項数\(n\)の等比数列\( \{ a_n \} \)の和\(S_n\)は、
\(r \neq 1\)のとき
\(\displaystyle S_n = \frac{a(r^n-1)}{r-1} = \frac{a(1-r^n)}{1-r} \)
\(r = 1\)のときは
\(S_n = na \)




この等比数列の和は公式も重要ですが、導出も重要です!この後、ド定番の応用問題「(等差数列)×(等比数列)の和」を求める際に同じ方法を使います。ある式操作でキレイに求められるので面白いですよ。
(証明)
「導出が重要」と言いましたが、ポイントだけ押さえておけばOKです。
\(S_n = a + ar + ar^2 + ar^3 + \cdots + ar^{n-2} + ar^{n-1} \)
ポイントは「この\(S_n\)に公比\(r\)を掛けたものを用意して引く」という操作です。
ちょっと丁寧に計算しましょう。\(S_n\)に公比\(r\)を掛けたものは次のようになります。
\(rS_n = r( a + ar + ar^2 + ar^3 + \cdots + ar^{n-2} + ar^{n-1} ) \)
\(rS_n = ar + ar^2 + ar^3 +ar^4 + \cdots + ar^{n-1} + ar^n \)(←右辺は分配法則で計算)
これを先ほどの\(S_n\)から引きます。
\(\quad S_n = a + ar + ar^2 + ar^3 + \cdots + ar^{n-2} + ar^{n-1} \)
\(-) rS_n =\quad ar + ar^2 + ar^3 + \cdots + ar^{n-1} + ar^n \) …※
※を1項ずつずらしているのがミソです。
そうするとわかりやすいですが、真ん中の\(ar + ar^2 + ar^3 +ar^4 + \cdots + ar^{n-1}\)の部分が、引くことで全部消えてしまいます!
なので、残るのは
\(S_n-rS_n = a -ar^n \)
\( (1-r)S_n = a(1-r^n) \)
\(r \neq 1\)のとき、両辺を\( (1-r) (\neq 0)\)で割れば、
\(\displaystyle S_n = \frac{a(1-r^n)}{1-r} \)(終)
分母、分子を「ー(マイナス)」でくくれば、それぞれ\(-(r-1)\)、\(-a(r^n-1)\)となるので、
\(\displaystyle S_n = \frac{-a(r^n-1)}{-(r-1)} = \frac{a(r^n-1)}{r-1} \)(終)
また、\(r = 1\)のときは、等比数列\( \{ a_n \} \)は\(a , a , a, \cdots , a\)という、初項\(a\)が並ぶ定数数列になります。
よって、このとき、\(S_n = a + a + \cdots +a = na\)(終)
問.初項\(a\)、公比\(r\)の等比数列\(\{a_n\}\)の一般項\(a_n = ar^{n-1}\)について。
\(a_n = ar^{n-1}= Ar^{n-1}-Ar^{n-2}\)となる\(A\)を\(a\)と\(r\)を用いて表せ。
また、\(a_k = ar^{k-1}= Ar^{k-1}-Ar^{k-2}\)に\(k=1,2,3,\cdots,n\)を代入した式を用いて\(\displaystyle a+ar+ar^2+\cdots+ar^{n-1} = \frac{a(r^n-1)}{r-1} \)となることを示せ。ただし、\(r \neq 1\)かつ\(r \neq 0\)とする。
答え
\(\displaystyle A=\frac{ar}{r-1}\)、証明は省略。
等比数列の和の公式を使う際のコツ
等比数列の和の公式は\(\displaystyle \frac{a(r^n-1)}{r-1}\)と \(\displaystyle\frac{a(1-r^n)}{1-r} \)のどちらを使うのか?
どちらを使っても問題なく計算できるのですが、
公比\(r\)について、\(r > 1\)のときは\(\displaystyle \frac{a(r^n-1)}{r-1}\)、\(r<1\)(「ー(マイナス)」も含む)のときは\(\displaystyle\frac{a(1-r^n)}{1-r} \)を使った方が計算しやすいです。
理由は簡単、分母(分子も、ですが)が「+」になるからです。



ま、どっちでもいいなら、どっちか覚えておけばいいや。
ではなく、どちらも使えるようにしておきましょう。



「ー(マイナス)」がからむと計算ミスしやすくなります。なるべくミスをしにくい計算方法で計算するように心がけましょう!計算も考えながらやると格段に計算ミスが減ります。ま、計算ミスをそのまま放置しておきたいなら別にいいですけどね。



…。
r=1のときの和naの意味は?
「等比数列の和の公式」と言っているのに\(r=1\)を考えるのはナンセンスな気もします…。
\(r=1\)のときは等比数列でもなんでもなく、定数数列になるからです。
ですが、導出方法を見たらわかりますが、どうしても\(S_n=\cdots\)の形にするために\((1-r)\)で割る必要があります。
ですので、一応\(r \neq 1\)のときに使える公式だ、というのは頭の片隅に入れておきましょう。



ちなみに、数学IIIの「極限」の分野で無限等比級数という話がでてきます。このとき、\(r=1\)で場合分けをする、という際に\(S_n=na\)という式を使ったりもします。
まとめ
等比数列の基本と公式の確認でした。
特に公式は「覚えるのが苦手…」という人も多いです。
文字の羅列ではなく、イメージを押さえながら実際に使って覚えていきましょう。



等比数列の和は導出も重要です。導出方法を覚えるついでに公式をしっかりと定着させましょう。






