複素数平面とベクトルの関係（内積まで）を解説！

2022年9月20日

複素数とベクトル…無関係に見えて、実は密接に関係してます。

この記事では、複素数とベクトルの関係について解説していきます。

ただし、押さえなければいけないポイントはそこまで多くありません。

複素数とベクトルの対応をサクッと把握しつつ、二つの異なる分野の結びつきを楽しみましょう！

複素数とベクトル「和・差」

たろぅ

せんせい！複素数平面とベクトルって関係しているってホントですか？

せんせ

んー…まぁそうですね。複素数平面での計算にベクトル的要素があるということがわかっていると理解しやすい部分があります。和や差はわかりやすいですね。

たろぅ

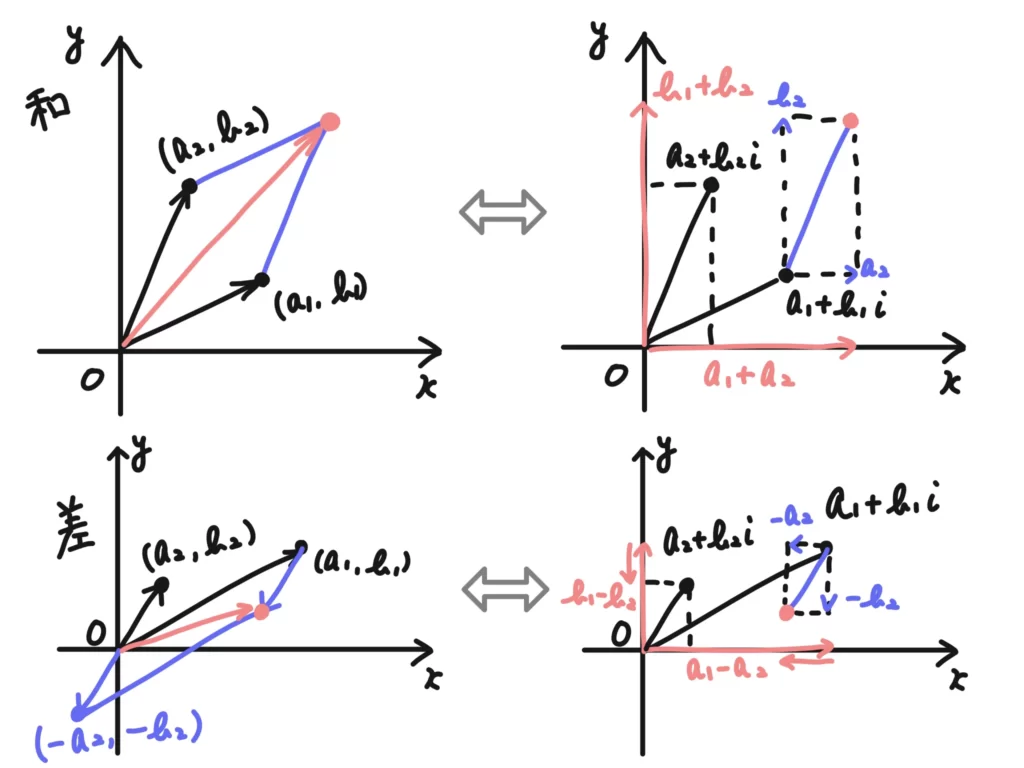
なるほど！

複素数とベクトル「実数倍」

せんせ

実数倍もわかりやすいです。複素数の実数倍とベクトルの実数倍は計算上しっかりリンクしてますね。

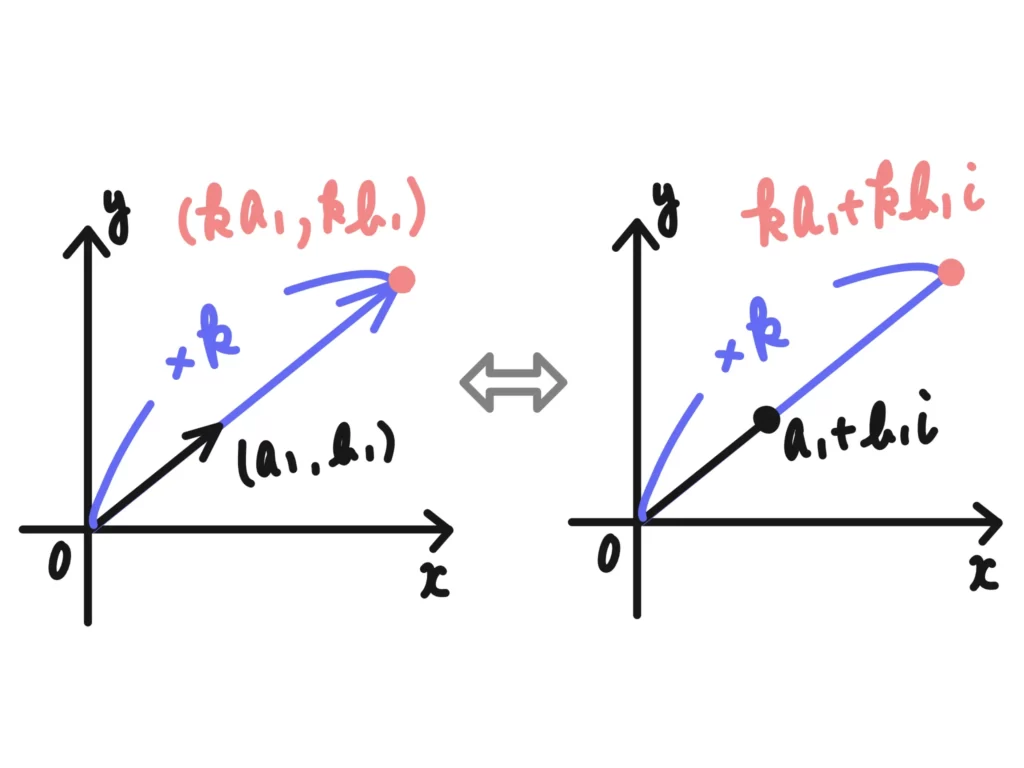
複素数とベクトル「内積」

たろぅ

でもまぁ、内積は無いでしょ？あんな複雑な計算、複素数には出てきませんよ。

せんせ

ふっふっふ…。

たろぅ

ま…まさか…。

せんせ

そう！そのまさかよ！あるんだな、これが！

あまり知られていませんが、複素数を使って内積を計算する方法もあります。

「複素数\(z_1=a_1 + b_1 i\)、\(z_2=a_2 + b_2 i\)」と「ベクトル\(\overrightarrow{a}=(a_1 , b_1)\)、\(\overrightarrow{a}=(a_2 , b_2)\)」の内積\(a_1a_2+b_1b_2\)の対応を考えていきます。

結論から言うと、\(z_1\)に\(z_2\)の共役な複素数\(\bar{z_2}\)を掛けたときの実部になります。

\( z_1 \bar{z_2} = (a_1 + b_1 i)(a_2 – b_2 i)\)

\( z_1 \bar{z_2}= a_1a_2+b_1b_2 + \{-(a_1b_2-b_1a_2)\}i \)

（↑計算は自分でやってみてください。虚部をー（マイナス）でくくったのは見栄え良くするためであまり意味はありません）

ちなみに、極形式表示と「回転＋拡大・縮小」の計算を使うとちょっと面白いことがわかります。

「極形式表示？」というひとはこちら、「回転＋拡大・縮小？」というひとはこちらをご覧ください。

\(z_1=r_1(\cos{\theta_1}+i\sin{\theta_1})\)、\(z_2=r_2(\cos{\theta_2}+i\sin{\theta_2})\)とすると、

\( \bar{z_2}=r_2\{\cos{(-\theta_2)}+i\sin{(-\theta_2)}\}\)なので、

\( z_1 \bar{z_2} = r_1r_2\{\cos{(\theta_1-\theta_2)}+i\sin{(\theta_1-\theta_2)}\}\)

\( z_1 \bar{z_2} = r_1r_2\cos{(\theta_1-\theta_2)}+ir_1r_2\sin{(\theta_1-\theta_2)}\)

となり、確かに実部は\(r_1r_2\cos{(\theta_1-\theta_2)}\)ですので、内積の定義と一致します。面白いですね。

（正確には\( \theta_1-\theta_2 \)は任意の角なので、成す角と一致するとは限りませんが、計算上は一致します。このあたりが「なんで？」と思う人はこちらの加法定理の記事の偏角の説明をご覧ください。）

こうなると「虚部は？」と思うかもしれません。

\( r_1r_2\sin{(\theta_1-\theta_2)} \)は絶対値をとれば、実は外積の大きさになります。が、実際には外積は空間じゃないと意味がないので、こちらに正しい解釈を与えるのは難しいかな、と思います。

\( r_1r_2\sin{(\theta_1-\theta_2)}=-(a_1b_2-b_1a_2) \)で計算できるのは面白いですけどね…絶対値をとればベクトル\(\overrightarrow{a}=(a_1 , b_1)\)、\(\overrightarrow{a}=(a_2 , b_2)\)が張る平行四辺形の面積になります。

せんせ

まぁ、正直言ってあまり使いません。