PR
複素数平面(ガウス平面)とは？何が役に立つの？基本を丁寧に説明
２０２２年度高校入学生から新教育課程になりますが、今までの「数学B」は内容をおよそ１.５倍〜２倍に膨らませた形で「数学B」と「数学C」の２科目に別れて勉強することになります。
ですので、このブログでも新教育課程に対応した内容をどんどん発信して、少しでも生徒・先生方の助けになれば、と思います。
そこで、いくつかの記事に分けて、新教育課程数学Cの「複素数平面」の解説をしていきます。これは今まで数学IIIで理系だけ習っていた内容ですが、新教育課程で文系の生徒も習うことになりました。
まずは複素数平面の基本について説明していきます。特にこの記事で説明する極形式表示は複素数平面の重要な表示方法ですので、しっかりと理解してください。
目次
複素数平面（ガウス平面）とは？
たろぅ…うーん。
せんせどうかしました？
たろぅいえ、さっきの授業で複素数平面を教わったんですが…。
せんせわかりませんでしたか？
たろぅいやぁ…言ってることはわかるんですけどね…。
せんせん？じゃあなにか問題でも？
たろぅなんかこう、それを考えてなにが嬉しいのか、イマイチわかりません。
せんせんー…。まぁもっと勉強を進めたらわかるんですが、とりあえず少し話をしますか。
たろぅお願いします！
複素数とは、虚数単位\(i\)を使って次のような形に表せる数のことです。
複素数とは、\(a+bi\)の形で表せる数。ただし、\(a\)、\(b\)は実数、\(i\)は虚数単位とする。
複素数についてはこちらの記事もあわせてご覧ください。
あわせて読みたい
複素数とは？「二乗すると-1」になる数って？
「二乗すると−１になる数って…そんなものあるわけないじゃないか！」と思ったアナタ…その通りです。 少なくとも実数の範囲では、ですが。 この記事では、「二乗すると−…
このとき、\(a+bi\)の\(a\)を実部、\(b\)を虚部といいます。
複素数平面とは、横軸を実軸、縦軸を虚軸として「複素数を平面上の点に対応させる」というものです。
もう少し丁寧に言うと、複素数\(a+bi\)を、実部\(a\)を横方向の座標、\(b\)を縦方向の座標にとった点\((a , b)\)と対応させる、という話です。
\(a+bi \Leftrightarrow\) 点\((a , b)\)
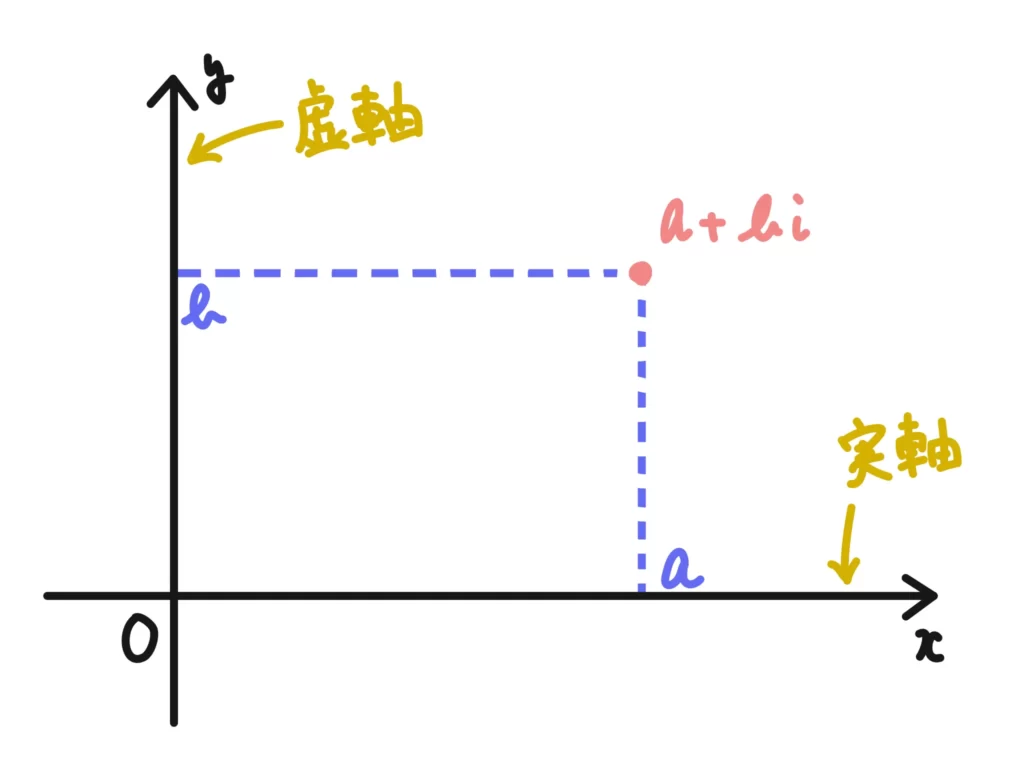
このようにして定めた平面を「複素数平面」といいます（大学では「複素平面」や「ガウス平面」といったりします）。
また、原点からの距離を絶対値といい\(z=a+bi\)の絶対値を \(|z|\)と書きます。
絶対値は原点からの距離なので、\( |z| = \sqrt{a^2+b^2}\)で計算することができます。
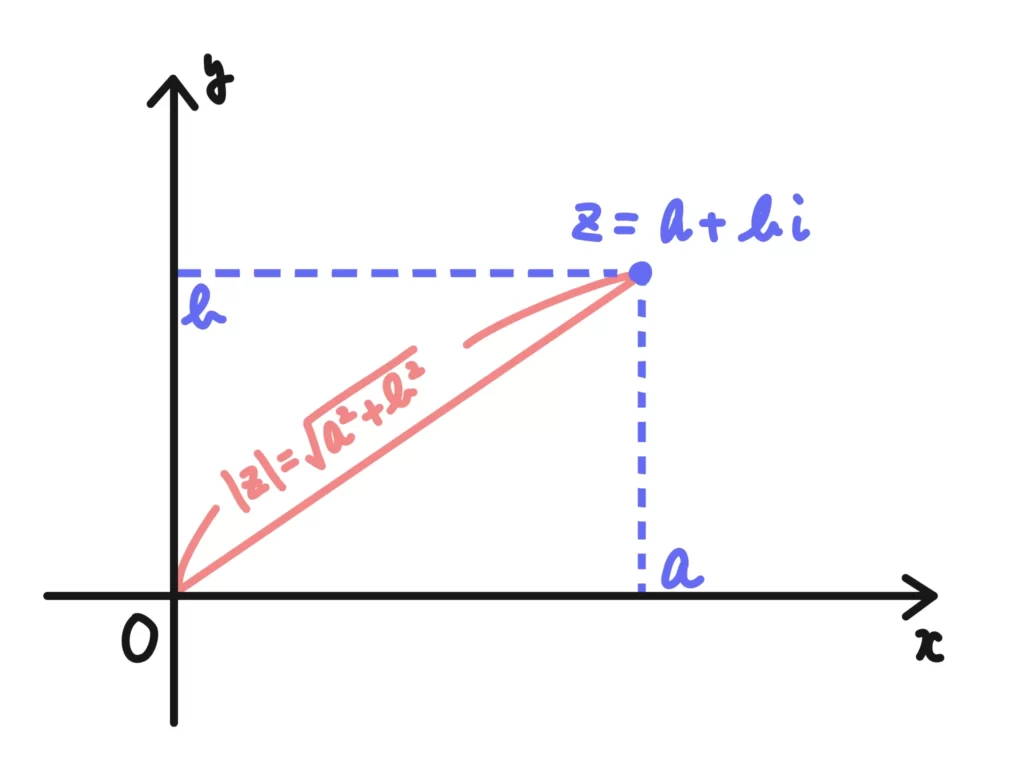
たろぅここまではわかったんですけどね。特に「絶対値は原点からの距離」というのがそのまま複素数平面上で定義できるのは面白いです。
せんせでは、「極形式表示」の話までしてみましょうか。
数学をモチーフにしたオシャレなオリジナルグッズも販売中です！おかげさまで好評頂いてます！
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ！
極形式表示
複素数\(a+bi\)を座標平面上の点\((a , b)\)に対応させるのはわかりやすい考え方なのですが、複素数平面が威力を発揮するのは複素数を極形式表示をしたときです。
極形式は、「原点からの距離＝絶対値」と「\(x\)軸正の方向と成す角＝偏角」の二つの要素で点の位置を定める方法です。
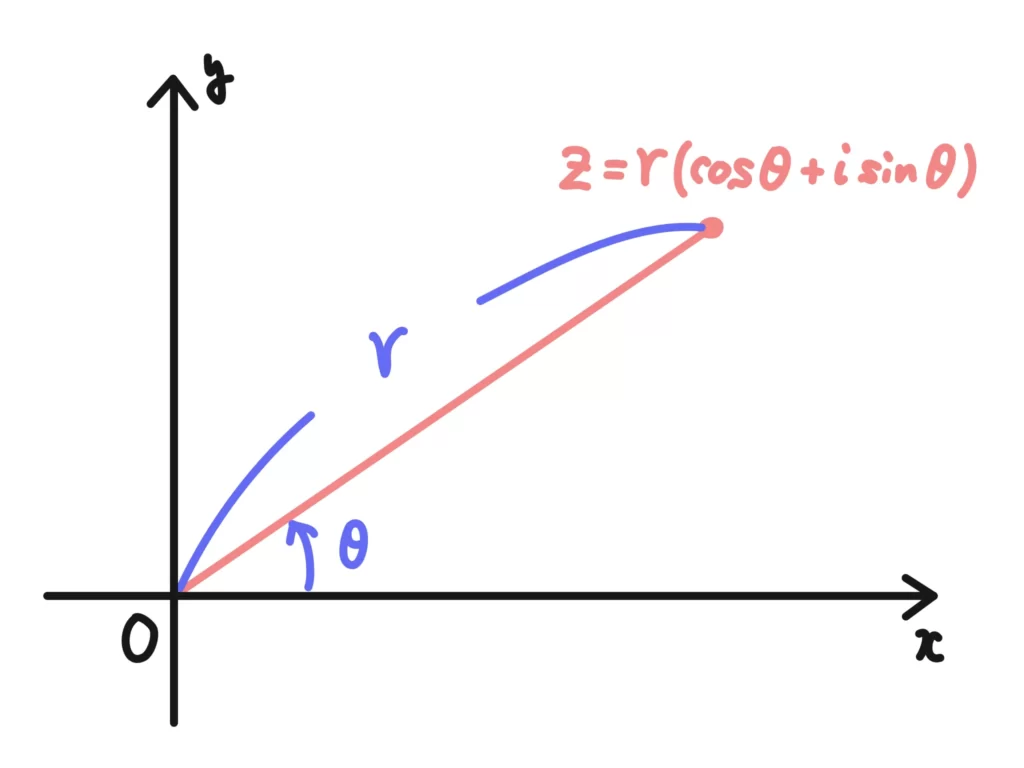
具体的に極形式で表す際は、次のような形で表します。
極形式表示
原点からの距離\(r\)と偏角\(\theta\)を用いて、
\(z = r(\cos{\theta} + i \sin{\theta} )\)
の形で表す方法を「極形式表示」という。
表現として、\(z\)の偏角を\(arg(z)\)と書くことがある。
ただし、\(r \geq 0 \)、\( 0 \leq \theta \leq 2 \pi \)とする。\(-\pi \leq \theta \leq \pi\)でもよい。この条件はなくても間違い、とまでは言えないが、極形式表示を一意にする（\(r\)にマイナスを許したり、\(\theta\)に範囲がないと、何通りも表せる）ためにつけておくことが多い。（※）
（※）の補足．偏角は一般角\(\theta+2n\pi\)（\(n\)は整数）の形で置くこともある。具体的には\(n\)乗根を求めるときに一般角で表示しないと、\(n\)個の解が出てこない。
たろぅこの辺がよくわかんないんですよね。まずこの形\(z = r(\cos{\theta} + i \sin{\theta} )\)の意味がちょっと分かりにくいです…。
いくつか考える方向性がありますので、お好みの考え方で理解してください。
考え方１「\(z = r\cos{\theta} + i r\sin{\theta}\)とみなす」
\(z = r(\cos{\theta} + i \sin{\theta} )\)を展開して、
\(z = r\cos{\theta} + i r\sin{\theta}\)とします。そして、\( z = a+bi = r\cos{\theta} + i r\sin{\theta}\)と比べると、
\( a = r\cos{\theta}\)、\(b = r\sin{\theta}\)となります。
これは、次の図のように\(r\)と\(\theta\)を使って\(x\)座標、\(y\)座標を定める、という考え方になります。
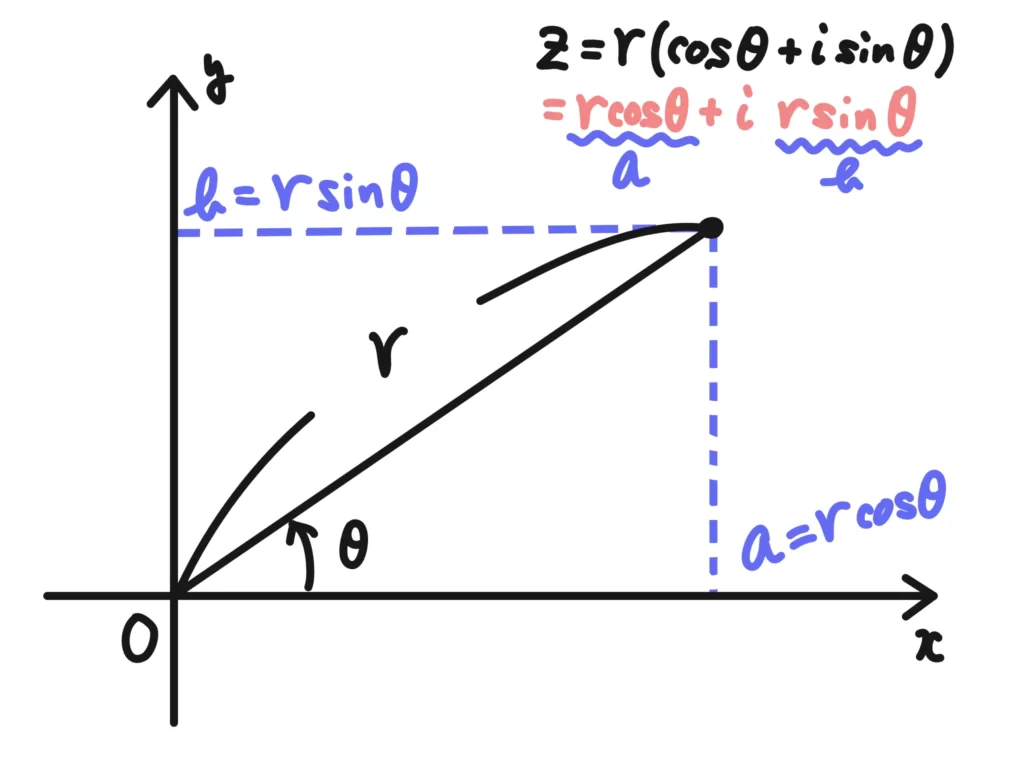
物理の勉強をしている人はこの考え方がしっくりくるかもしれません。
普通の\(xy\)平面やベクトルでもこの考え方を使ったりもしますので、慣れておいて損はないと思います。
考え方２．「\(\theta\)回転＋\(r\)倍」
複素数平面的にはこっちの考え方の方が、後々の「回転」「拡大・縮小」に繋がるのでオススメです。
まずは\(r=1\)とした\(z=\cos{\theta} + i \sin{\theta}\)から考えていきます。実はこの形は結構重要です。
先ほどと同様に\( z = a+bi = \cos{\theta} + i \sin{\theta}\)と比較すると、
\( a = \cos{\theta}\)、\(b = \sin{\theta}\)となりますが、重要なのはこれが「単位円上にある点を表す」ということです。
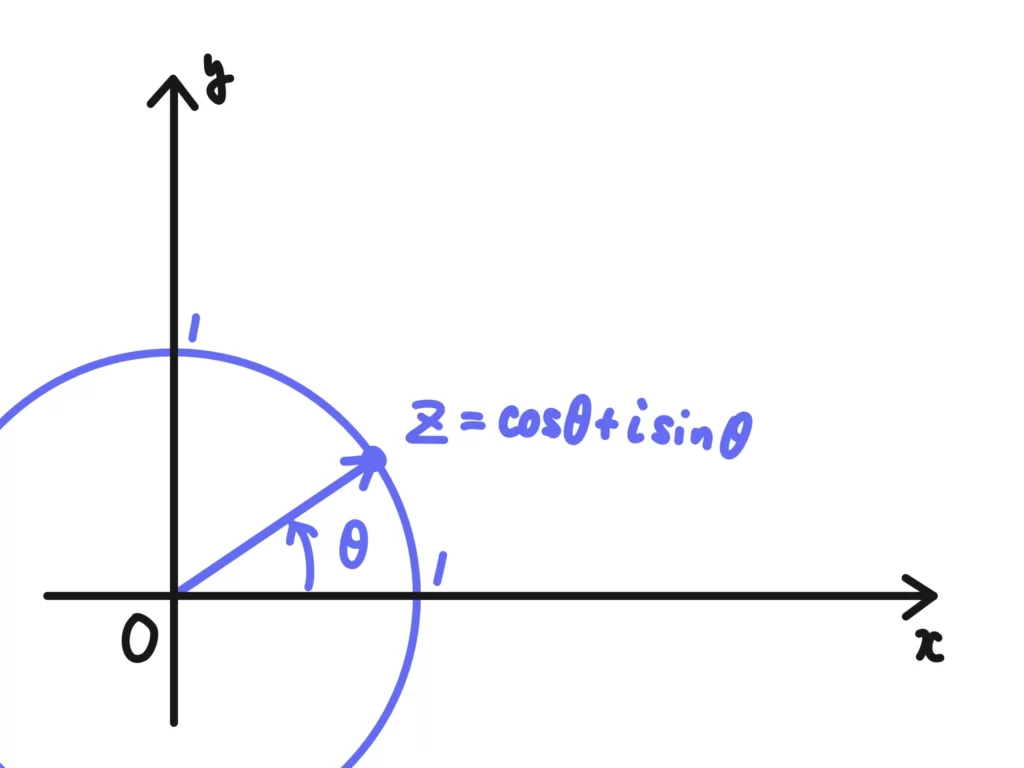
単位円上の点で方向を定めつつ、絶対値を\(r\)倍して求める点の座標まで届かせるイメージですね。
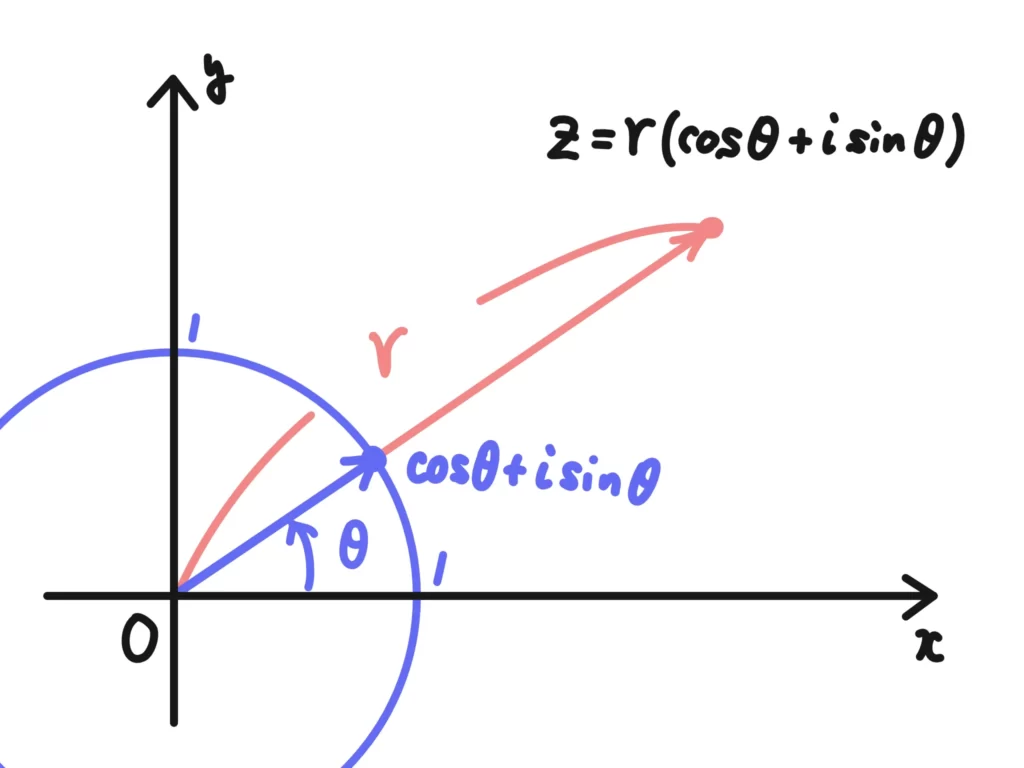
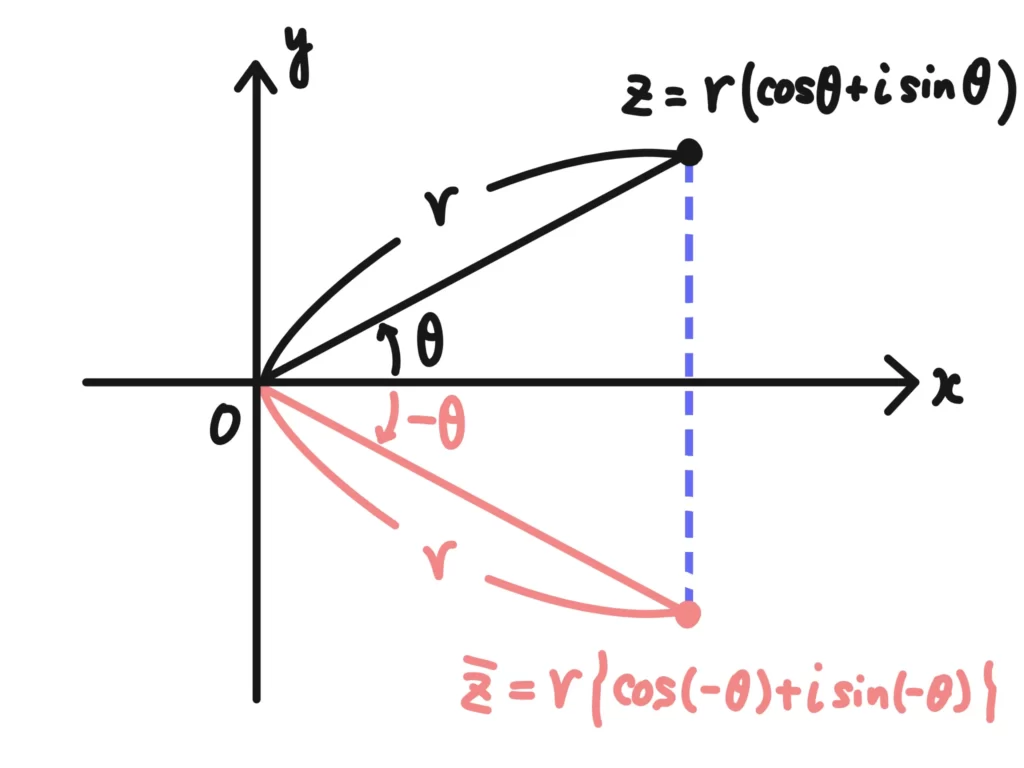
ちなみに、\(z = r(\cos{\theta} + i \sin{\theta} )\)の共役な複素数\(\bar{z}\)は、図からすぐに
\( \bar{z} = r \left\{ \cos{(-\theta)} + i \sin{(-\theta)} \right\} \)になることがわかります。
たろぅんー…なんでこんなわかりにくい形にするんでしょう？三角関数まで混じってわけわかんないです。 \( a+bi \)の形を点\((a , b)\)とした方がわかりやすいと思うんですが…。
せんせまぁ、確かに書くのも長いですしね…。でも、極形式の方が有用性が高いんですよ。
確かに形は複雑に見えますが、その分「絶対値」と「偏角」の情報が瞬時にわかる、というのは重要です。
なぜ重要かと言うと「回転」に関わる部分になるからです。
こちらの記事で解説していますが、複素数平面では複素数の積を「回転＋拡大・縮小」という意味にとらえることができます。詳しくはこちら。
あわせて読みたい
複素数平面では「積＝回転？」なぜ回転を表すのかを説明
複素数とは、「二乗すると\(-1\)になる虚数単位\(i\)」という数を使って表される、次のような形をした数です。 \( a+bi\)（ただし、\(a\)、\(b\)は実数） 「虚数（実在…
この「回転＋拡大・縮小」がわかれば、積、逆数、共役な複素数、累乗根、などが図形的な意味をもつようになり、理解が深まります。
ここまで理解ができれば、複素数平面が断然楽しくなってきます。
極形式表示への変換方法
極形式への変換は、「絶対値」と「偏角」がわかればOKです。
絶対値は\( |z| = | a+bi | =\sqrt{a^2+b^2}\)で計算できるので簡単ですが、偏角を読むのはちょっと大変です。
これについては慣れていくしかないかな、と思いますが、偏角の読み方は数学IIで習う「三角関数の合成」と同じです。有名角の直角三角形の比は分かるようにしておきましょう。
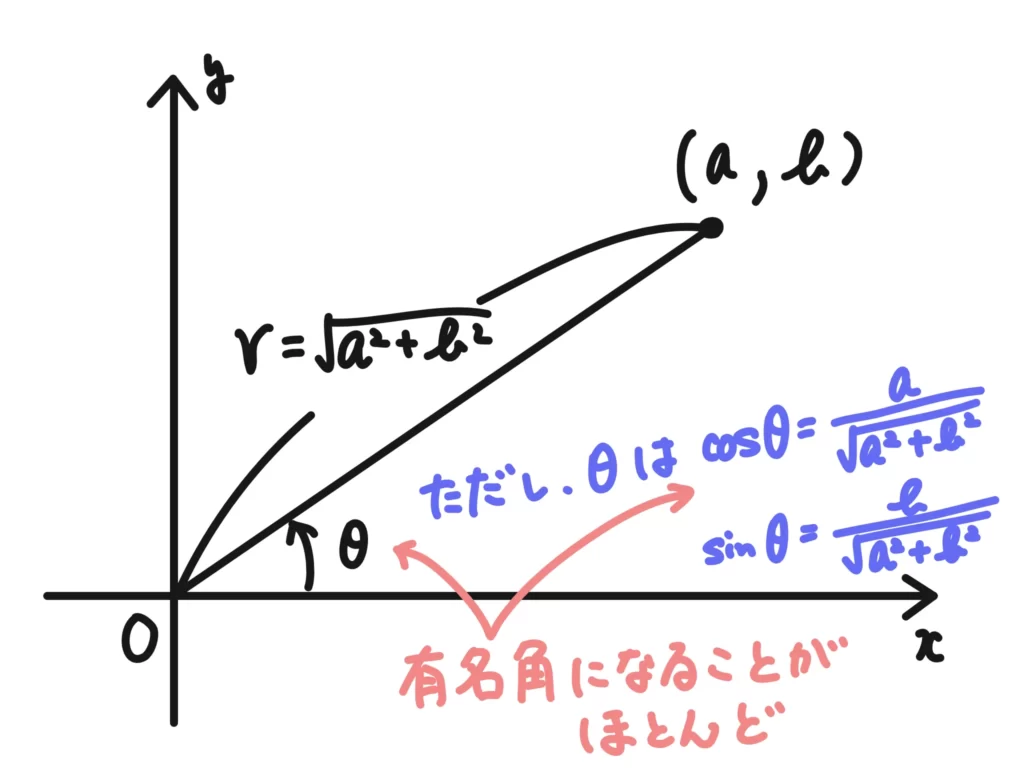
せんせいくつか練習問題も載せておきます。
問．次の複素数を極形式表示せよ。\( 1 + i \)。
答え
図を描く方がいいです。三角関数の合成に慣れている人は大丈夫だと思います。
（解）
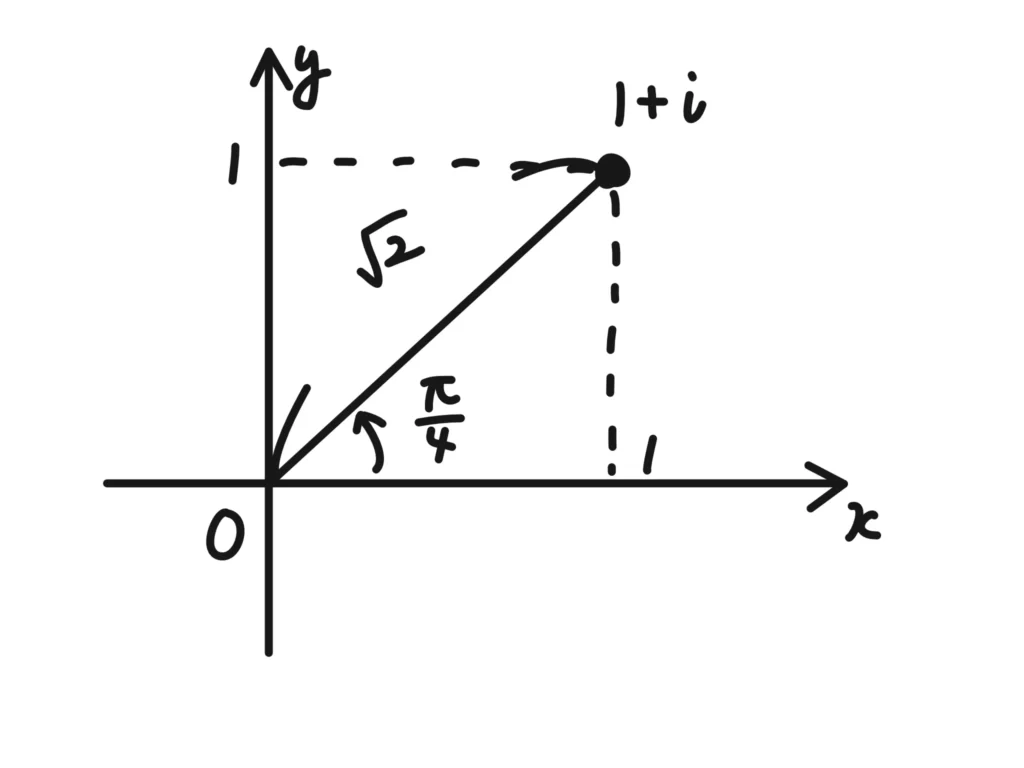
よって、 \(\displaystyle 1 + i = \sqrt{2} \left( \cos{\frac{\pi}{4}}+i \sin{\frac{\pi}{4}} \right) \)
問．次の複素数を極形式表示せよ。\(\displaystyle -\frac{1}{2} + \frac{\sqrt{3}}{2}i \)。
答え
これも図を描けばOKです。三角関数の合成に慣れている人は大丈夫だと思います。
（解）
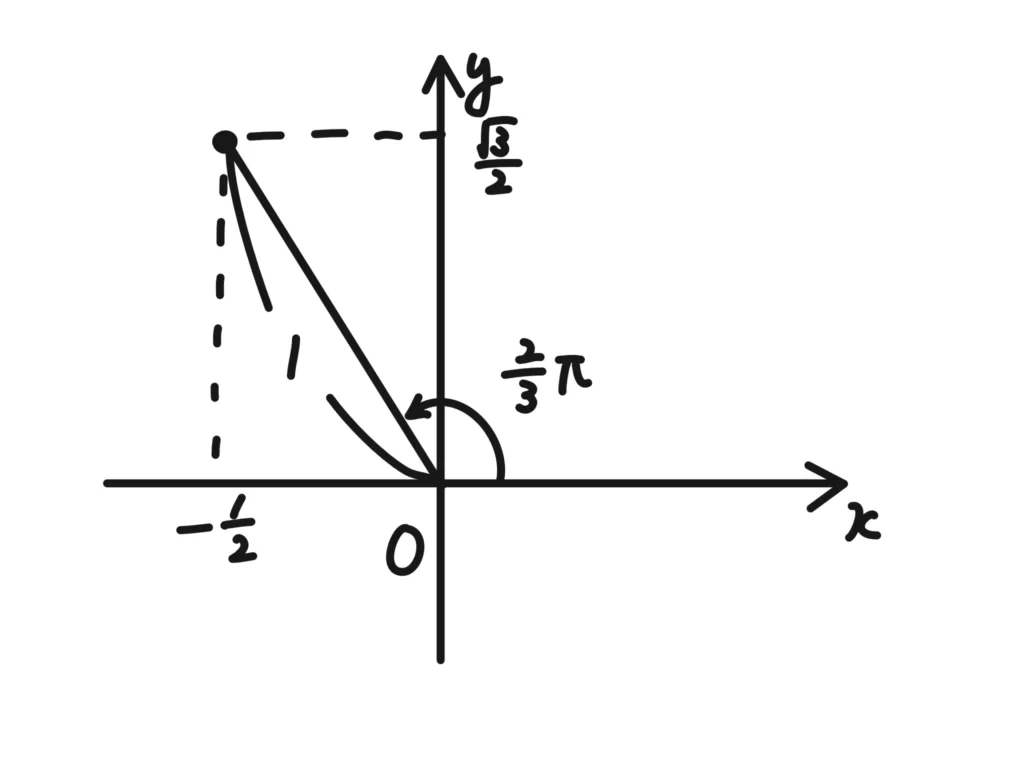
よって、 \(\displaystyle -\frac{1}{2} + \frac{\sqrt{3}}{2}i = \cos{\frac{2}{3}\pi}+i \sin{\frac{2}{3}\pi} \)
問．次の複素数を極形式表示せよ。\( \sqrt{3} -i \)。
答え
（解）
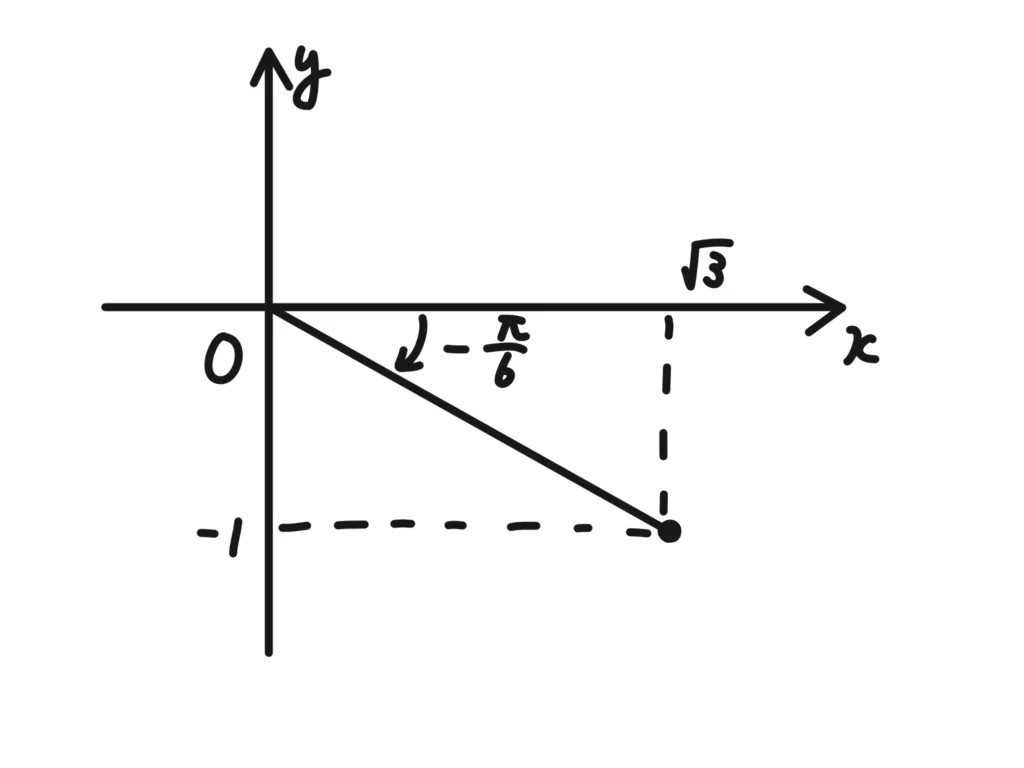
よって、 \(\displaystyle \sqrt{3} -i = 2 \left\{ \cos{ \left( -\frac{\pi}{6} \right) }+i \sin{\left( -\frac{\pi}{6} \right) } \right\} \)
複素数平面の何が嬉しい？
複素数平面は数に対する概念の広がりと座標との対応が嬉しい点ですね。
複素数は一つの数で２つの要素を持っている（実部と虚部）ので、平面上の点を表現できます。普通の数は要素を一つしか持っていません。
ですので、ただ複素数の計算（足し算、引き算、実数倍、掛け算、割り算）をするだけで点の移動を表現することができます。
余談になりますが、複素数やベクトル、行列のように、複数の要素を１セットにして扱うのは想像以上に便利です。複数の要素を１セットにしたものに対する演算を研究すると、効率がとても上がります。
プログラミングでも「配列」という変数が存在しますが、これはいくつかの変数をセットにしたものです。機能的には変数を一つ一つ定義すれば配列を使わなくても同じことができますが、配列を使った変数定義はどのプログラミング言語でも必須です。
それだけ「ひとつのものにまとめて考える」というのは効率上重要なんですね。
まとめ
複素数平面の基本と極形式についてまとめました。
複素数平面は一つ一つのことをバラバラと覚えていたら意味がありません。
それぞれの考え方がどんどん繋がっていくので、複雑ではありますが、学べば学ぶほど面白い分野です。
ぜひ、一つ一つの考え方をマスターして、それを繋げていって「複素数平面マスター」になってください！
あわせて読みたい
複素数平面とベクトルの関係（内積まで）を解説！
複素数とベクトル…無関係に見えて、実は密接に関係してます。 この記事では、複素数とベクトルの関係について解説していきます。 ただし、押さえなければいけないポイン…
あわせて読みたい
面白くてオススメの数学本・マンガ
最近よく「オススメの数学の本はありますか？」という質問を受けます。 正直、あんまり本は読まないのですが、これまで読んできた中で「これは面白い！」というオススメ…
複素数平面をしっかり学習したら、ぜひこちらも読んでみてください。
『数学ガールの秘密ノート』シリーズは基本から丁寧に話が進んでいくのでわかりやすいですし、なにより物語として面白いのでオススメです！
リンク
ちょっと一息
数学をモチーフにしたオシャレなオリジナルグッズも販売中です！おかげさまで好評頂いてます！
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ！
また、このブログで活躍してるクマのLINEスタンプも販売しています！ぜひ一度見てみてください！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
