PR
複素数平面では「積=回転?」なぜ回転を表すのかを説明
複素数とは、「二乗すると\(-1\)になる虚数単位\(i\)」という数を使って表される、次のような形をした数です。
\( a+bi\)(ただし、\(a\)、\(b\)は実数)
「虚数(実在しない数)なんか考えてどうすんの?」と思うかもしれませんが、「複素数平面」で「複素数を平面上の点として表現する」ことにより、その意味と考え方を爆発的に広げることができます。
なにせ、今まで「二つの数の組」が必要だったのに「一つの数」で表現できるようになるのですから。
とりわけ重要な性質が「積」です。
複素数平面では「積」を「回転+拡大・縮小」とみなすことができます。
この記事では複素数の積と回転、拡大・縮小の関係をわかりやすく説明していきます。
極形式表示をもう一度…
 せんせ
せんせ今日は複素数の「積」です。



掛け算ですね!簡単ですよ!ここで基本的な内容は勉強しましたからね!



ん?「掛け算が回転と拡大・縮小を表す」って話はしましたっけ?



ん?



ん?



回転?拡大・縮小?



…はい!極形式の復習から〜!!



あう…極形式ってなんだっけ…?
極形式については、こちらをご覧ください。

極刑式は複素数\(z\)を絶対値\(r\)と偏角\(\theta\)を使って、
\(z = r (\cos{\theta}+i\sin{\theta})\)
の形で表す方法です。
この形で積をとると「回転+拡大・縮小」を表現することができるのです。
複素数の積が「回転+拡大・縮小」を表す?



それでは極形式表示した複素数の積と「回転+拡大・縮小」の意味を押さえていきましょう!



お願いしまーす。
\( z_1 = r_1 (\cos{\theta_1}+i\sin{\theta_1})\)、\( z_2 = r_2 (\cos{\theta_2}+i\sin{\theta_2})\)とすると、
\( z_1 z_2= r_1 (\cos{\theta_1}+i\sin{\theta_1})\cdot r_2 (\cos{\theta_2}+i\sin{\theta_2})\)
\( = r_1 r_2 (\cos{\theta_1}\cos{\theta_2}+i\cos{\theta_1}\sin{\theta_2}\)
\(\quad\quad+i\sin{\theta_1}\cos{\theta_2}+i^2\sin{\theta_1}\sin{\theta_2})\)(←展開)
\( = r_1 r_2 \{ (\cos{\theta_1}\cos{\theta_2}-\sin{\theta_1}\sin{\theta_2})\)
\(\quad\quad+i(\sin{\theta_1}\cos{\theta_2}+\cos{\theta_1}\sin{\theta_2}) \}\)(←\(i\)がひっついてるとことひっついてないとこで整理)
\( = r_1 r_2 \{ (\cos{(\theta_1+\theta_2)}+i\sin{(\theta_1+\theta_2)} \}\)
(↑加法定理。「加法定理って?」という人はこちら。)
よって、\( z_1 z_2= r_1 r_2 \{ (\cos{(\theta_1+\theta_2)}+i\sin{(\theta_1+\theta_2)} \}\)



んー…これってどういうことなんですかね?
この計算で、\(z_1z_2\)で計算された複素数\(z_3\)の情報をみてみましょう。
つまり、\(z_3= r_1 r_2 \{ (\cos{(\theta_1+\theta_2)}+i\sin{(\theta_1+\theta_2)} \}\)の絶対値と偏角を読み取ります。
この形と極形式の基本の形\(z = r (\cos{\theta}+i\sin{\theta})\)を比較すると、
絶対値→\(r_1 r_2\)、偏角→\(\theta_1+\theta_2\)
になっています。
つまり、\(z_1\)の目線で考えると、
「絶対値は\(r_2\)倍、偏角は+\(\theta_2\)」されていることになります。
これが、複素数の積を「回転+拡大・縮小」と表現した意味です。



複素数を掛けるだけで、
絶対値は「掛けた複素数の絶対値倍」
偏角は「掛けた複素数の偏角を足す」
が一気に表現できることになります。



なるほど…便利ですね。
それでは少し、具体例を挙げてみましょう。
例.\(\displaystyle z_1=2\left(\cos{\frac{\pi}{6}}+i \sin{\frac{\pi}{6}}\right)\)に色々な複素数を掛けてみましょう。
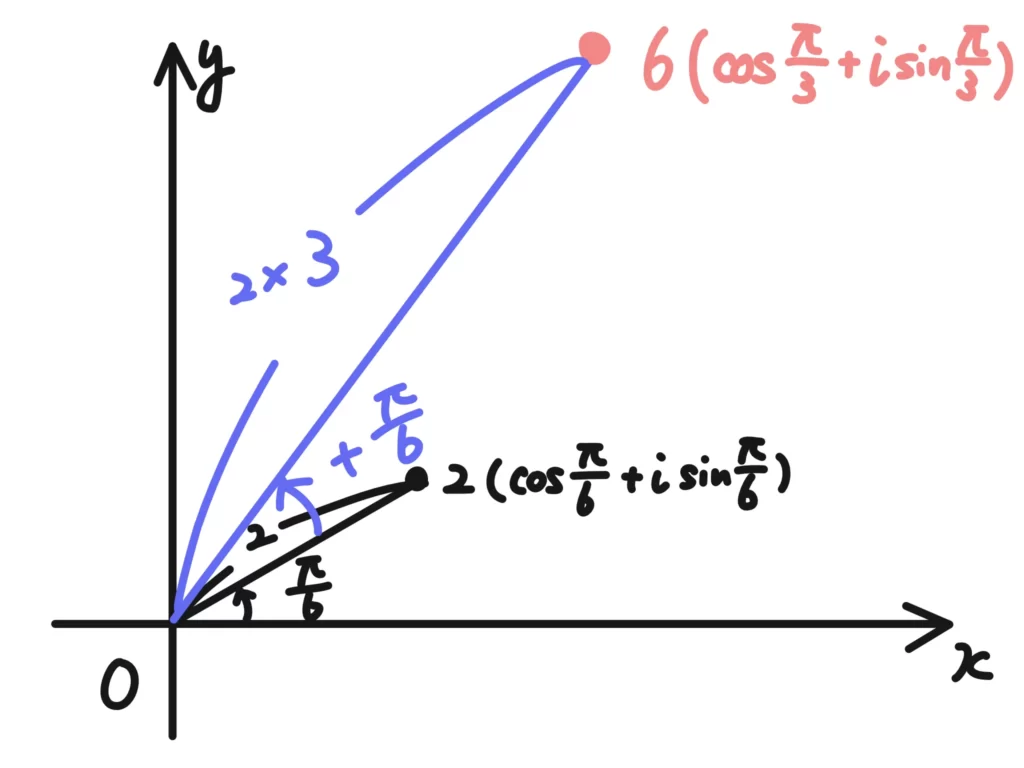
(1) \(\displaystyle z_2=3\left(\cos{\frac{\pi}{6}}+i \sin{\frac{\pi}{6}}\right)\)を掛けると次のようになります。
\(\displaystyle z_1z_2=2\cdot 3 \left\{ \cos{\left(\frac{\pi}{6}+\frac{\pi}{6}\right)}+i \sin{\left(\frac{\pi}{6}+\frac{\pi}{6}\right)}\right\}\)
\(\displaystyle z_1z_2=6 \left(\cos{\frac{\pi}{3}}+i \sin{\frac{\pi}{3}}\right)\)

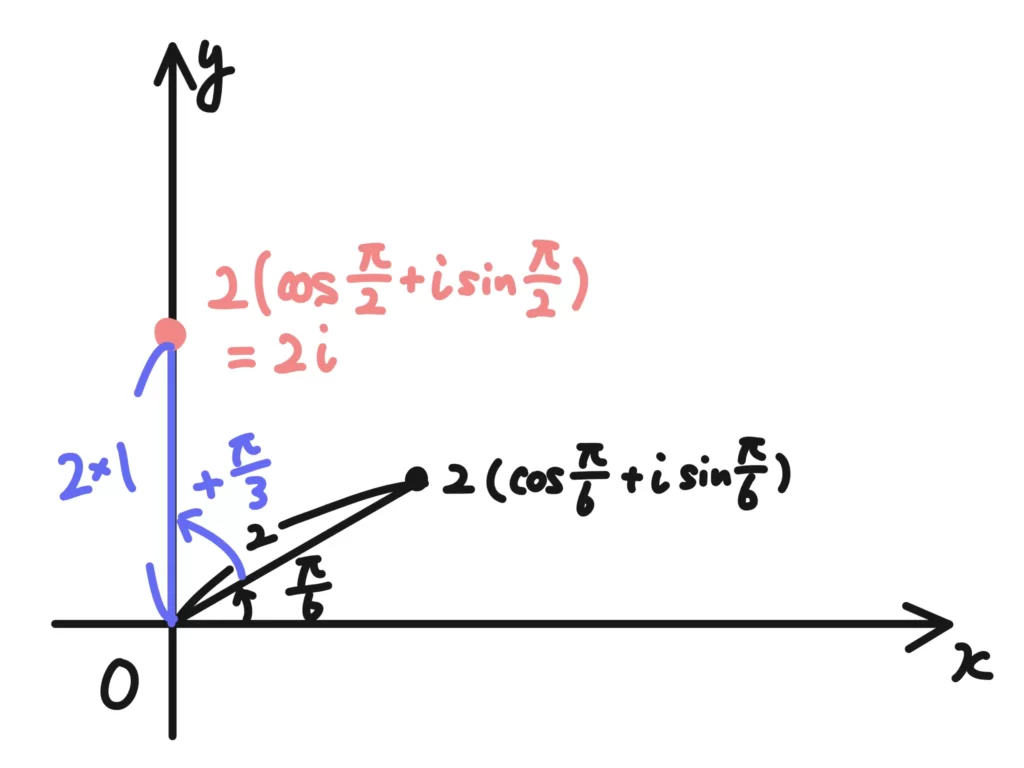
(2) \(\displaystyle z_3 = \cos{\frac{\pi}{3}}+i \sin{\frac{\pi}{3}}\)を掛けると次のようになります。絶対値は1なので「回転」のみになりますが、この「絶対値1の複素数を掛けて回転のみ表現」はよく使います。
\(\displaystyle z_1z_3=2 \left\{ \cos{\left(\frac{\pi}{6}+\frac{\pi}{3}\right)}+i \sin{\left(\frac{\pi}{6}+\frac{\pi}{3}\right)}\right\}\)
\(\displaystyle z_1z_3=2 \left(\cos{\frac{\pi}{2}}+i \sin{\frac{\pi}{2}}\right)=2i\)
今回はあえて\(\displaystyle\cos{\frac{\pi}{2}}=0\)、\(\displaystyle \sin{\frac{\pi}{2}}=1\)を使って\(a+bi\)の形に戻してみました。
偏角\(\displaystyle \frac{\pi}{2}\)となっているのがわかりやすいと思います。

「回転+拡大・縮小」で複素数平面をもう一度捉え直そう



この「複素数の積=回転+拡大・縮小」とみなすことで、基本的な複素数平面の考え方が綺麗に意味を持ちはじめます。
逆数と「回転+拡大・縮小」
逆数については、実際に計算してみたいと思います。
\(z = r(\cos{\theta}+i\sin{\theta})\)について、
\(\displaystyle \frac{1}{z} = \frac{1}{r(\cos{\theta}+i\sin{\theta})}\)
\(\displaystyle \quad = \frac{1}{r}\frac{\cos{\theta}-i\sin{\theta}}{(\cos{\theta}+i\sin{\theta})(\cos{\theta}-i\sin{\theta})}\)
\(\displaystyle \quad = \frac{1}{r}\frac{\cos{\theta}+i(-\sin{\theta})}{\cos^2{\theta}+\sin^2{\theta}}\)
\(\displaystyle \frac{1}{z} = \frac{1}{r} \{ \cos{(-\theta)}+i\sin{(-\theta)} \}\)
(↑ \(\cos{\theta} \Leftrightarrow \cos{(-\theta)}\)、\(-\sin{\theta} \Leftrightarrow \sin{(-\theta)}\)を使った)
ということで逆数をとると、絶対値は\(\displaystyle \frac{1}{r}\)倍、偏角は\(-\theta\)になります。
これに、先ほどの積の結果を合わせると、
\( \displaystyle \frac{z_1}{z_2} = \frac{r_1}{r_2} \{ \cos{ (\theta_1-\theta_2) } + i \sin{ (\theta_1-\theta_2) } \} \)
となります。
実数倍と「回転+拡大・縮小」
複素数の実数倍には「ベクトルの延長」の意味合いがありますが、これは積の「回転+拡大・縮小」の「拡大・縮小」のみを行っていると思ってもらえればOKです。
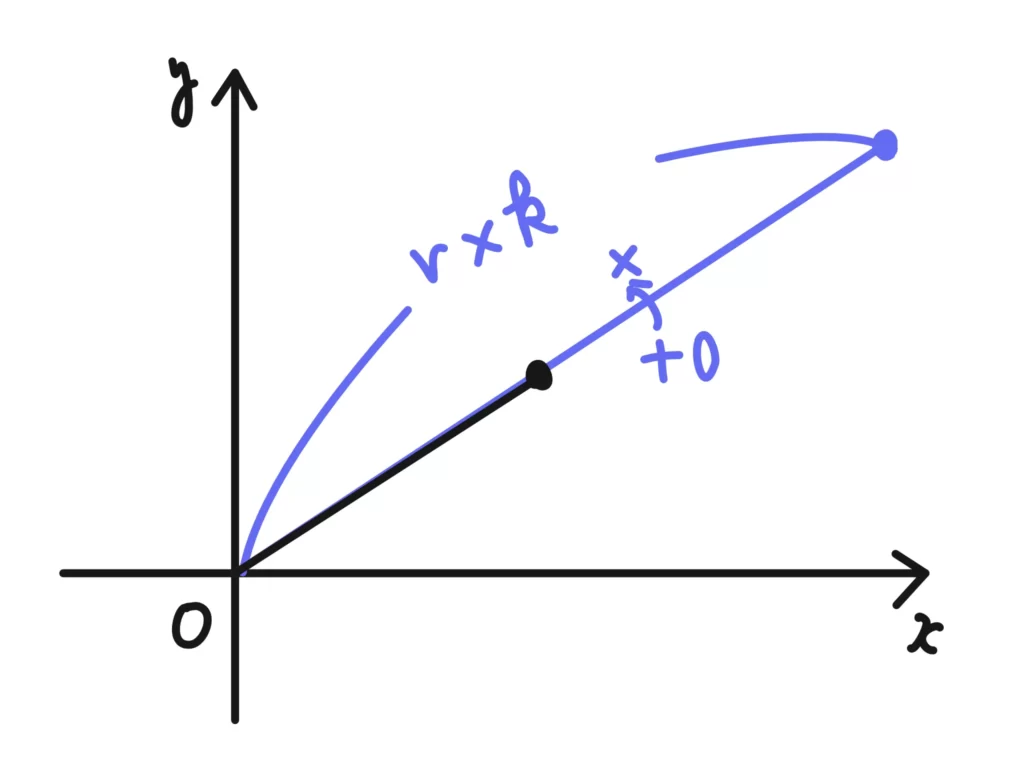

\(k=k(\cos{0}+i\sin{0})\)とみなせば、絶対値が\(k\)倍、回転は+0になります。
\(kz = kr \{ \cos{(\theta+0)} + i \sin{ (\theta + 0)}\}=kr(\cos{\theta} + i \sin{\theta}) \)
となり、偏角を変えずに絶対値だけ\(k\)倍していることがわかります。
-1や虚数単位iと「回転+拡大・縮小」
こちらの記事でなぜ「マイナス×マイナス=プラスになるのか?」について説明しました。

これを複素数平面の目線から解説してみます。
ベクトルを勉強した人はわかると思いますが、ー(マイナス)には「180°逆方向の向き」という意味合いがあります。
これを複素数の極形式で表すと、
\(-1 = \cos{\pi} + i\sin{\pi}\)(度数表記の180°=弧度法の\(\pi\))
となります。\(\cos{\pi}=-1\)、\(\sin{\pi}=0\)ですから、確かに\(-1\)となっていますね。
つまり、\(-1\)は複素数の積で言うと絶対値は1倍(そのまま)、偏角は\(+\pi\)の「回転+拡大・縮小」になります。
よって、
\((-1)(-1)=(\cos{\pi} + i\sin{\pi})(\cos{\pi} + i\sin{\pi})\)
\(\quad=\cos{(\pi+\pi)} + i\sin{(\pi+\pi)}=\cos{2\pi} + i\sin{2\pi}=1\)
となります。
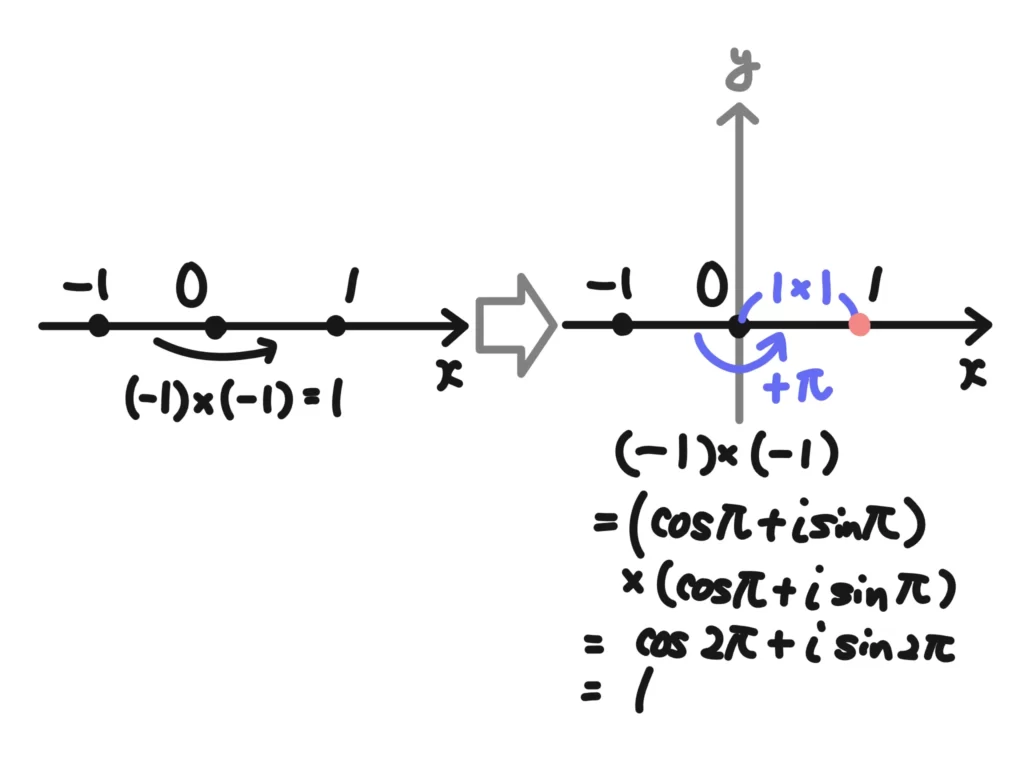
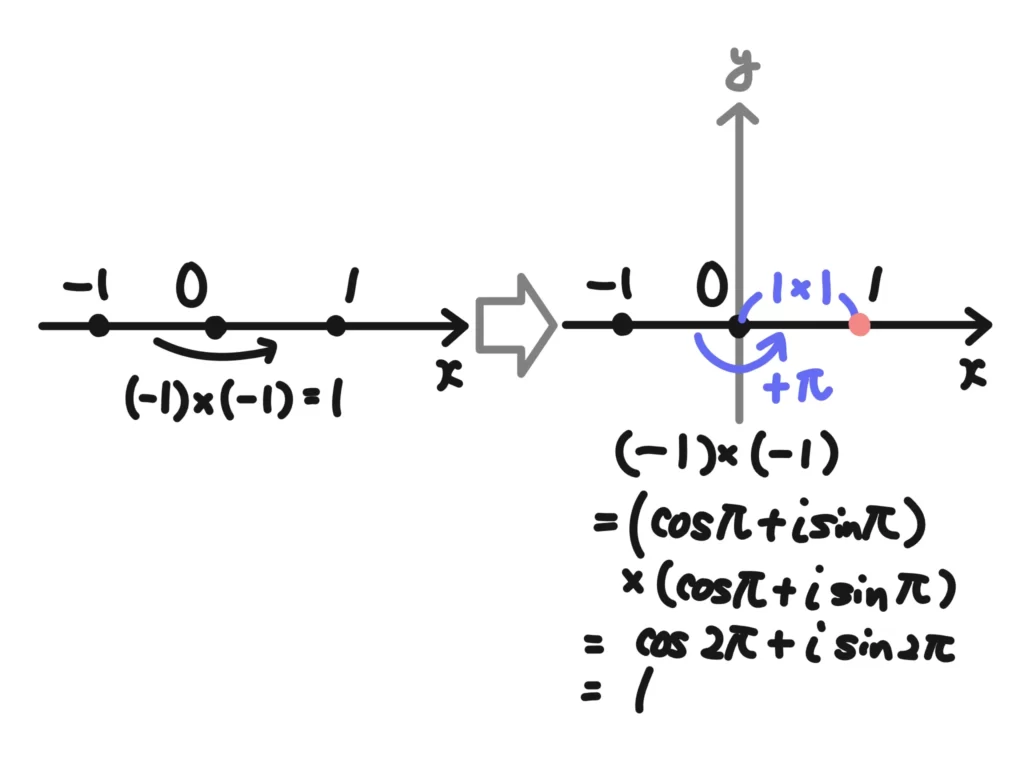
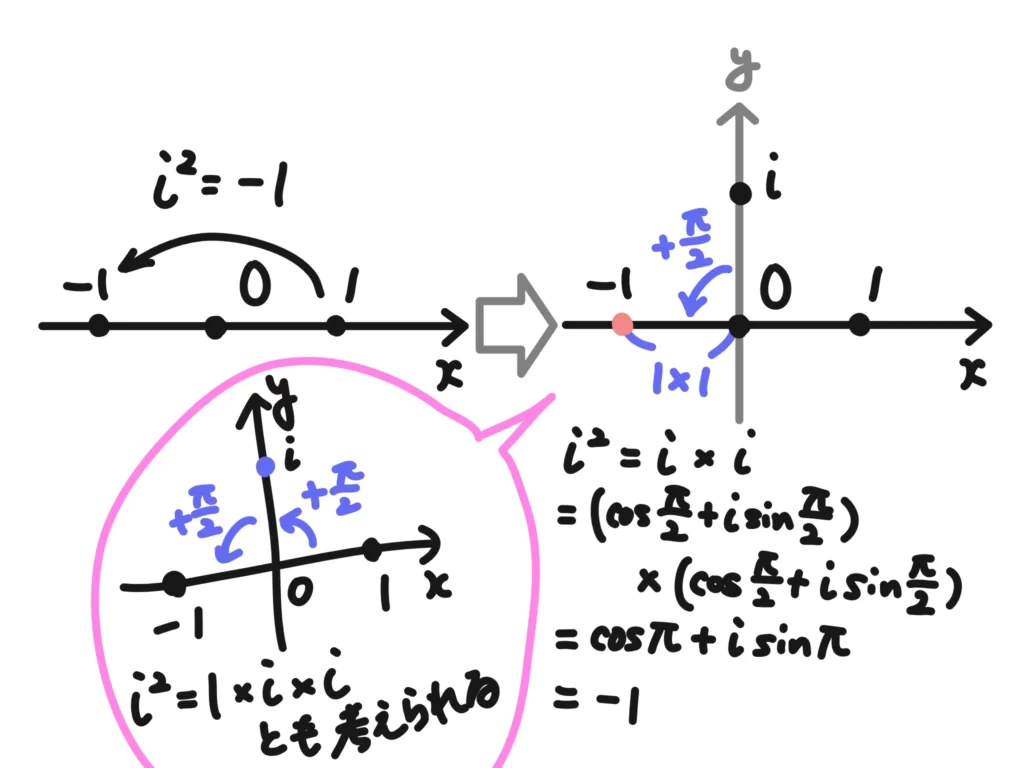
この考え方を使えば、\(i^2=-1\)となることも自然に説明ができます。
\(i\)を極形式表示すると\(\displaystyle i = \cos{\frac{\pi}{2}}+i \sin{\frac{\pi}{2}}\)となります。
つまり、\(i\)は複素数の積で言うと絶対値は1倍(そのまま)、偏角は\(\displaystyle+\frac{\pi}{2}\)の「回転+拡大・縮小」になります。
よって、
\(\displaystyle i^2 = i \cdot i = \left( \cos{\frac{\pi}{2}}+i \sin{\frac{\pi}{2}}\right)\left( \cos{\frac{\pi}{2}}+i \sin{\frac{\pi}{2}}\right)\)
\(\displaystyle \quad = \cos{ \left( \frac{\pi}{2}+\frac{\pi}{2} \right) }+i \sin{ \left( \frac{\pi}{2}+\frac{\pi}{2} \right) } = \cos{\pi} + i\sin{\pi} = -1\)
となります。




はぁ…。マイナス×マイナス=プラスになることや\(i^2=-1\)になることが「回転」で説明できるのは面白いですね!
まとめ
複素数の積は「回転+拡大・縮小」になる、ということについて説明しました。
ここを理解すれば、「回転+拡大・縮小」の計算にとどまらず、今まで複素数の「なんでこうなるのかよくわかんないな…」と思っていた部分も図形的な意味として解釈できます。
結果はシンプルですが、複素数平面を理解するための強力な武器ですので、しっかりと理解しておいてください!


複素数平面をしっかり学習したら、ぜひこちらも読んでみてください。
『数学ガールの秘密ノート』シリーズは基本から丁寧に話が進んでいくのでわかりやすいですし、なにより物語として面白いのでオススメです!



