加法定理の公式一覧と証明のポイント（偏角の扱いについての詳細も）

①の証明。\(\cos{(\alpha-\beta)}=\cos{\alpha} \cos{\beta} + \sin{\alpha}\sin{\beta}\)を示します。

（証明）

いきなりですが、次の図を見てください。

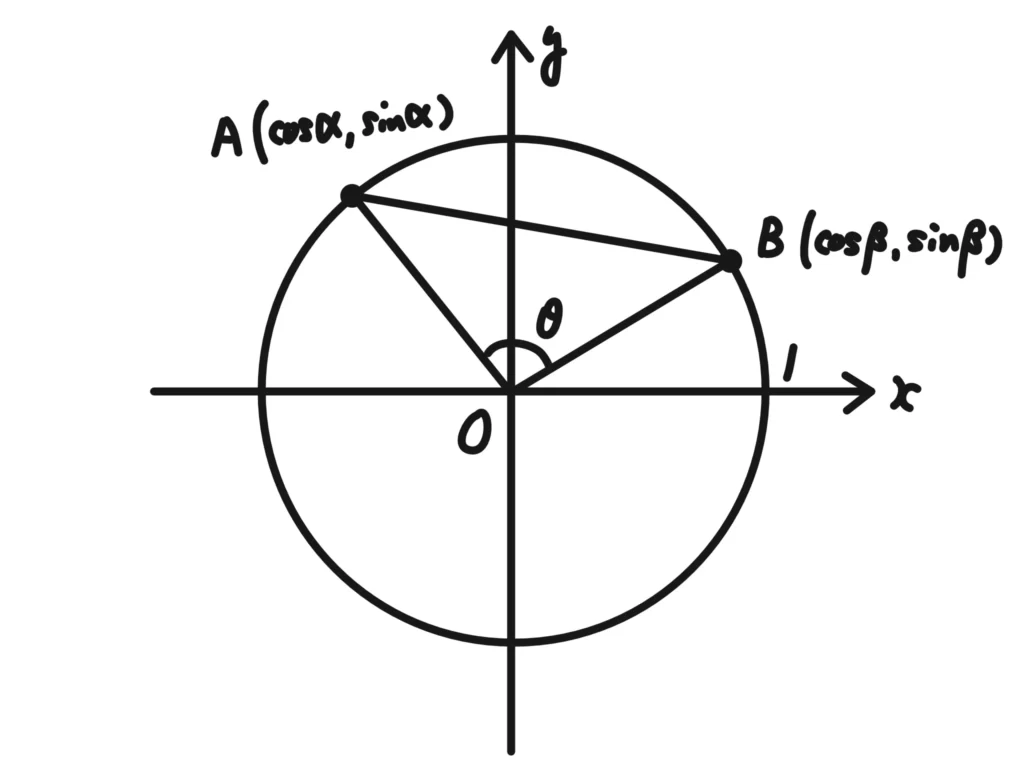
この単位円上の点A、Bと原点Oを使って、△OABを作ります。

そして、点A\((\cos{\alpha} , \sin{\alpha})\)、点B\((\cos{\beta} , \sin{\beta})\)とすると、

（\(\alpha\)、\(\beta\)ってどの角？という疑問は置いておいてください。とりあえず単位円上にあるので、コサイン、サインを使って座標を表せます。）

二点間距離の公式から

\( AB^2 = (\cos{\alpha}-\cos{\beta})^2+(\sin{\alpha}-\sin{\beta})^2\)

\( \quad = \sin^2{\alpha}+\cos^2{\alpha}+\sin^2{\beta}+\cos^2{\beta}\)

\( \quad\quad -2(\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta})\)

\( AB^2 = 2-2(\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta})\)…(i)

一方、余弦定理から

\(AB^2 = 1^2 + 1^2 -2 \cdot 1 \cdot 1 \cdot \cos{\theta}\)

\(AB^2 = 2 -2 \cos{\theta}\)…(ii)

①、②より

\(2-2(\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}) = 2 -2 \cos{\theta}\)

よって、\( \cos{\theta} = \cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta} \)…(iii)

ここで、\(\theta\)について、\(\theta \Rightarrow \alpha – \beta\)としてみます。

「これで問題ないんじゃないの？」と思うかもしれないが、実際のところ\(\alpha\)、\(\beta\)は一般角なので、\(\theta = \alpha – \beta\)となる保証はありません（\(\theta\)はあくまで図形的にできあがった△OABの内角のひとつ）。

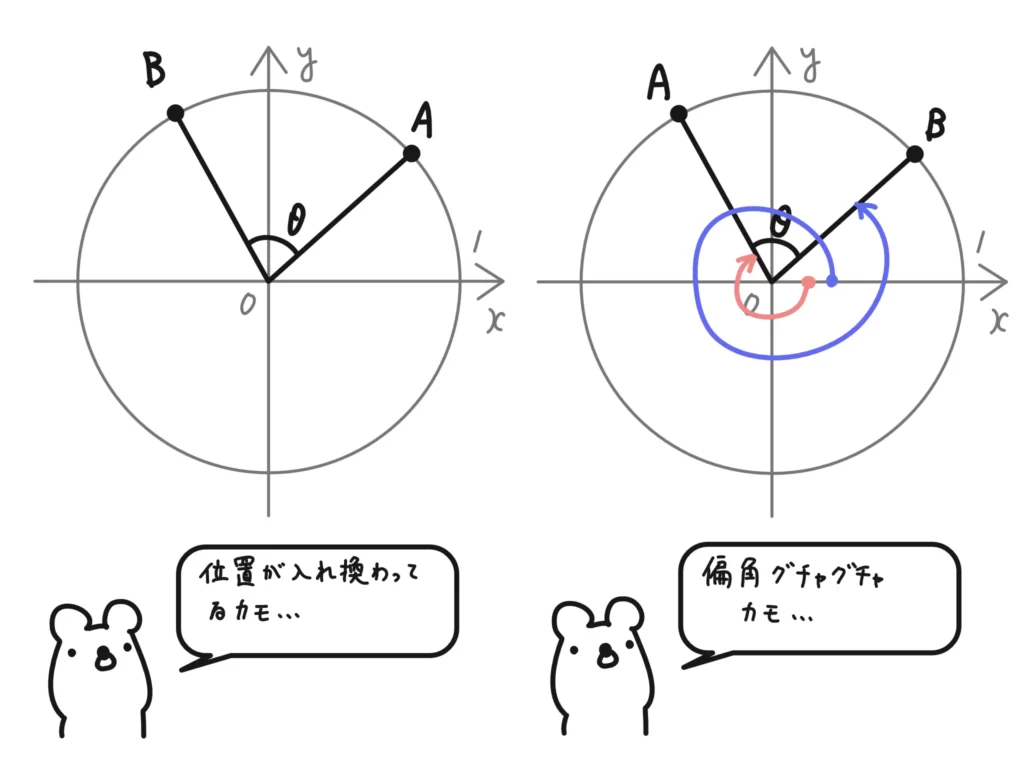
しかし、\(\theta \Rightarrow \alpha – \beta\)としても(iii)の式的には問題はありません。

なぜなら、\(\cos{}\)をとれば、\( \cos{\theta} = \cos{(\alpha – \beta)}\)になるからです。

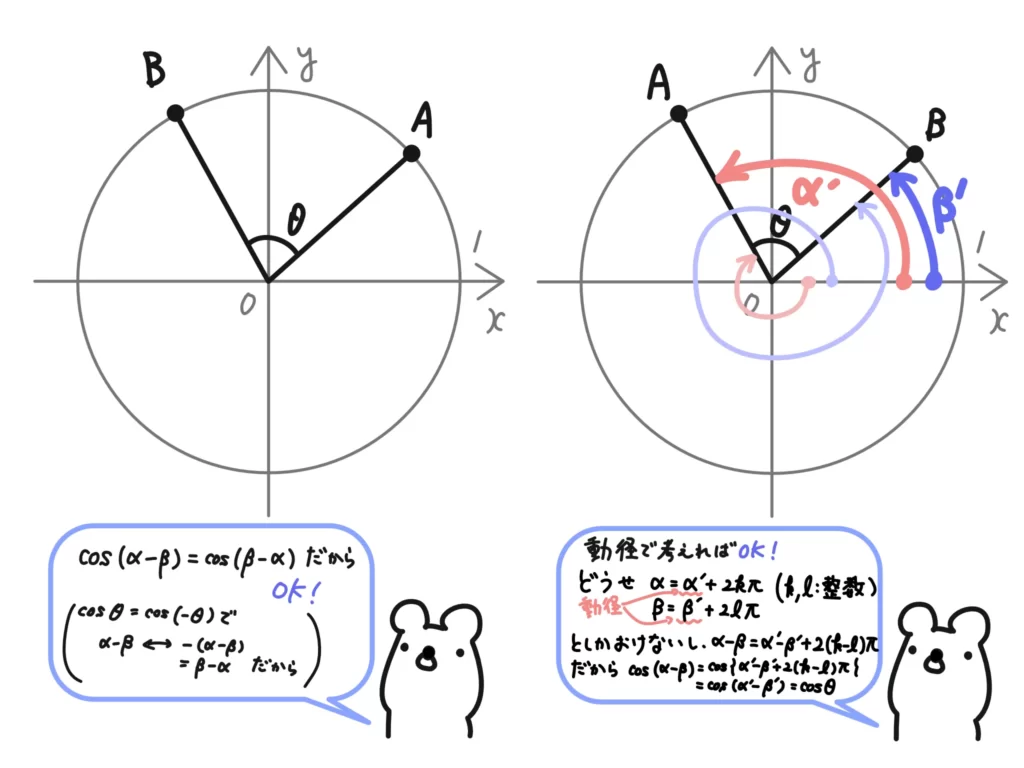
よって、\(\cos{(\alpha-\beta)}=\cos{\alpha} \cos{\beta} + \sin{\alpha}\sin{\beta}\)（①終）

（証明）

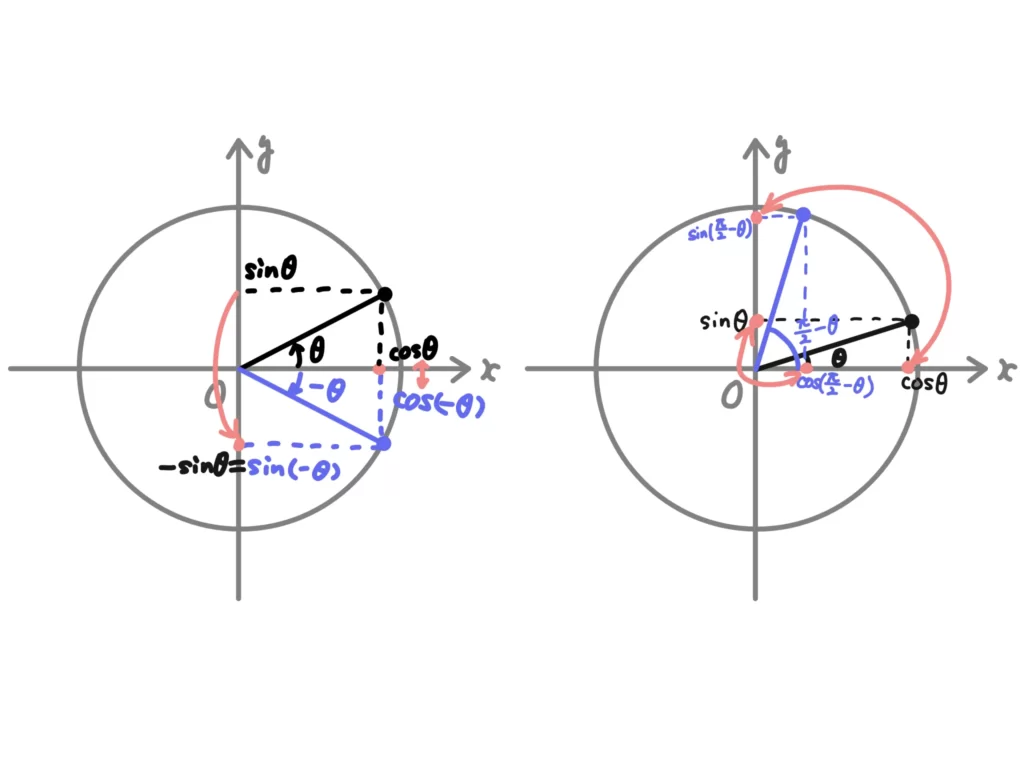
\(\sin{(-\theta)} = -\sin{\theta}\)、\(\cos{(-\theta)} = \cos{\theta}\)、

\(\displaystyle \sin{\left( \frac{\pi}{2}-\theta \right)}=\cos{\theta}\)、\(\displaystyle \cos{\left( \frac{\pi}{2}-\theta \right)}=\sin{\theta}\)、という性質を使っていきます。

\(\cos{(\alpha-\beta)}=\cos{\alpha} \cos{\beta} + \sin{\alpha}\sin{\beta}\)…(※)

の\(\beta \Rightarrow -\beta\)に置き換えます。

\(\cos{(\alpha+\beta)}=\cos{\alpha} \cos{(-\beta)} + \sin{\alpha}\sin{(-\beta)}\)

\(\cos{(\alpha+\beta)}=\cos{\alpha} \cos{\beta} – \sin{\alpha}\sin{\beta}\)（←欲しい式の一つ）

次に(※)の\(\displaystyle \alpha \Rightarrow \frac{\pi}{2}-\alpha\)に置き換えます。

\(\displaystyle \cos{\left( \frac{\pi}{2}-\alpha-\beta \right)}=\cos{\left( \frac{\pi}{2}-\alpha \right)} \cos{\beta} + \sin{\left( \frac{\pi}{2}-\alpha \right)}\sin{\beta}\)

\(\displaystyle \cos{\left\{ \frac{\pi}{2}-\left( \alpha+\beta\right) \right\}}=\sin{\alpha} \cos{\beta} + \cos{\alpha}\sin{\beta}\)

\( \sin{(\alpha+\beta)}=\sin{\alpha} \cos{\beta} + \cos{\alpha}\sin{\beta}\)（←欲しい式の一つ）

この式の\(\beta \Rightarrow -\beta\)に置き換えます。

\( \sin{(\alpha-\beta)}=\sin{\alpha} \cos{(-\beta)} + \cos{\alpha}\sin{(-\beta)}\)

\( \sin{(\alpha-\beta)}=\sin{\alpha} \cos{\beta} – \cos{\alpha}\sin{\beta}\)（←欲しい式の一つ）

（②終）

（証明）

仕上げにタンジェントの加法定理の証明をしますが、\(\displaystyle \tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\)と\(\tan{(-\theta)}=-\tan{\theta}\)の性質を使うだけです。

\(\displaystyle \tan{(\alpha+\beta)}=\frac{\sin{(\alpha+\beta)}}{\cos{(\alpha+\beta)}}\)

\(\displaystyle \quad = \frac{\sin{\alpha} \cos{\beta} + \cos{\alpha}\sin{\beta}}{\cos{\alpha} \cos{\beta} – \sin{\alpha}\sin{\beta}}\)

\(\displaystyle \quad = \frac{\frac{\sin{\alpha}}{ \cos{\alpha}} + \frac{\sin{\beta}}{\cos{\beta}} }{ 1- \frac{\sin{\alpha}}{\cos{\alpha}}\frac{\sin{\beta}}{\cos{\beta}}}\)（←\(\cos{\alpha} \cos{\beta}\)で割った）

\(\displaystyle \tan{(\alpha + \beta)} = \frac{ \tan{\alpha} + \tan{\beta} }{ 1 – \tan{\alpha} \tan{\beta} } \)（←欲しい式の一つ）

この式の\(\beta \Rightarrow -\beta\)に置き換えます。

\(\displaystyle \tan{(\alpha – \beta)} = \frac{ \tan{\alpha} + \tan{(-\beta)} }{ 1 – \tan{\alpha} \tan{(-\beta)} } \)

\(\displaystyle \tan{(\alpha – \beta)} = \frac{ \tan{\alpha} – \tan{\beta} }{ 1 + \tan{\alpha} \tan{\beta} } \)（←欲しい式の一つ）

ただし、以上の式変形中の分母は（分母）≠0とします。

（③終）

（証明）

図を使った証明方法です。

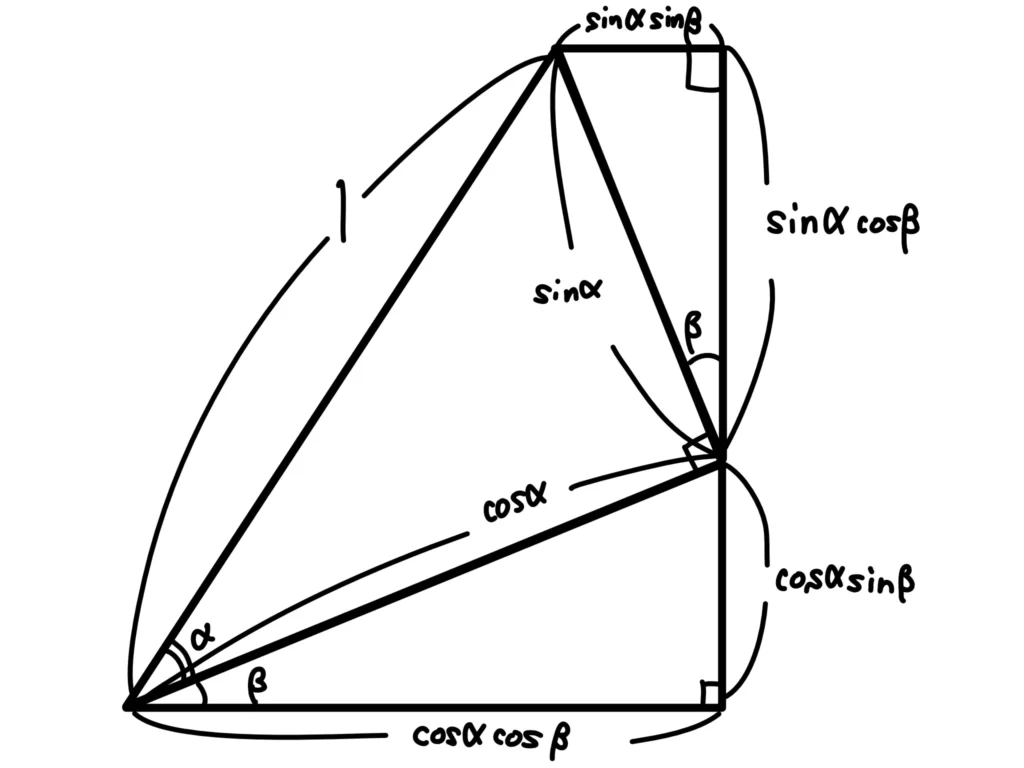
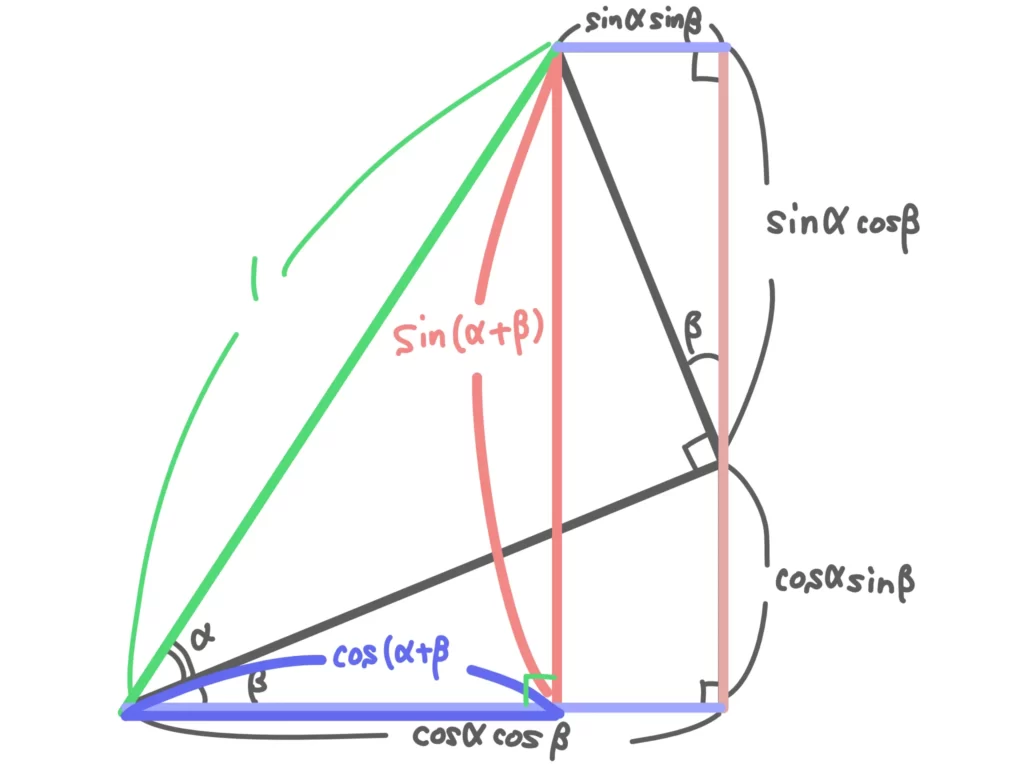
図より、\(\sin{(\alpha + \beta)}=\sin{\alpha} \cos{\beta} + \cos{\alpha}\sin{\beta}\)

\(\cos{(\alpha + \beta)}=\cos{\alpha} \cos{\beta} – \sin{\alpha}\sin{\beta}\)（終）

（証明）

三角形の面積を使ったアプローチです。

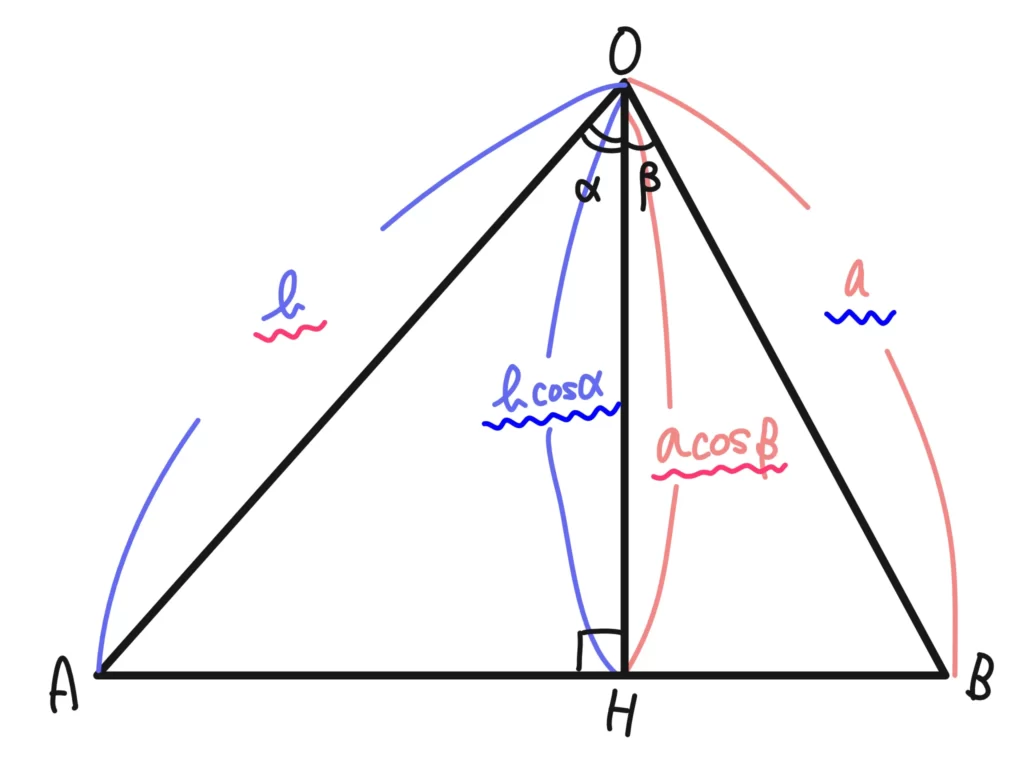
（△OABの面積）\(\displaystyle = \frac{1}{2}ba\sin(\alpha + \beta)\)…①

一方、

（△OABの面積）=（△OAHの面積）+（△OBHの面積）

上図の「赤い波線の辺のペア」と「青い波線の辺のペア」で面積公式を使うと、

（△OABの面積）\(\displaystyle = \frac{1}{2}b\cdot a\cos{\beta} \cdot \sin{\alpha} + \frac{1}{2}a\cdot b\cos{\alpha} \cdot \sin{\beta}\)

\(\displaystyle \quad = \frac{1}{2}ba ( \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta}) \)…②

①、②より

\(\displaystyle \frac{1}{2}ba\sin(\alpha + \beta)=\frac{1}{2}ba ( \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta}) \)

よって、\(\sin{(\alpha + \beta)}=\sin{\alpha} \cos{\beta} + \cos{\alpha}\sin{\beta}\)（終）