PR
コーシーシュワルツの不等式の「恐ろしくスマートな証明」
コーシーシュワルツの不等式…ご存じでしょうか？
有名な不等式なのですが、証明方法が結構面白いので、この記事で紹介していきたいと思います。
目次
コーシーシュワルツの不等式の証明
たろぅせんせい、「コーシーシュワルツの不等式」ってなんですか？
せんせあぁ、有名な不等式ですね。証明してみてください。
たろぅ（ん？今「証明してみてください」って言った？）あ、説明してくれるんですか？
せんせいや、式だけ教えるので証明してみてください。宿題として追加しておきます。
たろぅ…しまった、余計なことしたぁ。
せんせとりあえず、コーシーシュワルツの不等式は次のとおりです。
コーシーシュワルツの不等式
・\(a_1\)、\(a_2\)、\(b_1\)、\(b_2\)について、以下の不等式が成り立つ。
\( (a_1^2+a_2^2)(b_1^2+b_2^2) \geq (a_1 b_1 + a_2 b_2)^2 \)
・一般的に\(a_i\)、\(b_i\)\( (i=1 , 2 , \cdots , n) \)について、以下の不等式が成り立つ。
\( (a_1^2+a_2^2+ \cdots +a_n^2)(b_1^2+b_2^2 +\cdots +b_n^2) \geq (a_1 b_1 + a_2 b_2+ \cdots + a_n b_n)^2 \)
まずは\( (a_1^2+a_2^2)(b_1^2+b_2^2) \geq (a_1 b_1 + a_2 b_2)^2 \)について証明していきます。
不等式の証明
「不等式の証明」として証明するのがオーソドックスです。
不等式の証明の方法はこちらの記事をご覧ください。
あわせて読みたい
等式・不等式の証明の「正しい書き方」へのコツ
証明…響きがイヤですね。 実際に「証明」と聞いて「うわー…なんか色々書かないといけないやつでしょ？書き方も細かいし、イヤ！嫌い！」という人も（たくさん）いると思…
ということで、不等式の証明方法の基本に沿って証明していきます。
\( (a_1^2+a_2^2)(b_1^2+b_2^2) \geq (a_1 b_1 + a_2 b_2)^2 \)…①
（証明）
（左辺）ー（右辺）
\(= (a_1^2+a_2^2)(b_1^2+b_2^2) – (a_1 b_1 + a_2 b_2)^2 \)
\(= a_1^2 b_1^2+a_1^2 b_2^2+a_2^2 b_1^2+a_2^2 b_2^2 – (a_1^2 b_1^2 + 2a_1 b_1 a_2 b_2 + a_2^2 b_2^2) \)
\(= a_1^2 b_2^2+a_2^2 b_1^2 – 2a_1 b_1 a_2 b_2 \)
\(= a_1^2 b_2^2 – 2a_1 b_2 a_2 b_1+a_2^2 b_1^2=(a_1 b_2 – a_2 b_1)^2 \geq 0 \)
よって①は成り立つ。
等号成立は\( a_1 b_2 – a_2 b_1=0 \)、つまり\( a_1 b_2 = a_2 b_1\)のとき（終）
たろぅふぅ…不等式の証明ならなんとかできたぞ。最後の因数分解が長ったらしくて難しかったな…。
ベクトルを使った証明方法
ベクトルを使った証明もあります。こちらはかなり鮮やかです！
内積の成分計算も使うのでこちらの記事もあわせて読んでみてください！
あわせて読みたい
ベクトルの内積とは？【求め方や証明とイメージ】
ベクトルは便利で重要な考え方ですが、苦手な人が多い分野でもあります。 原因は「イメージ」と「その場での思考」が重要だからです。 その状況に応じた対応って苦手…。…
（証明）
\(\overrightarrow{a} = (a_1, a_2)\)、\(\overrightarrow{b} = (b_1, b_2)\)とする。
\(-|\overrightarrow{a}||\overrightarrow{b}| \leq \overrightarrow{a} \cdot\overrightarrow{b} \leq |\overrightarrow{a}||\overrightarrow{b}|\)より、
\( (\overrightarrow{a} \cdot \overrightarrow{b} )^2 \leq (|\overrightarrow{a}||\overrightarrow{b}|)^2 \)
\( |\overrightarrow{a}|^2|\overrightarrow{b}|^2 \geq (\overrightarrow{a} \cdot \overrightarrow{b} )^2 \)
\( (a_1^2+a_2^2)(b_1^2+b_2^2) \geq (a_1 b_1 + a_2 b_2)^2 \)
等号成立は\( \overrightarrow{a} \cdot\overrightarrow{b} = \pm |\overrightarrow{a}||\overrightarrow{b}|\)のときなので、成す角が0°または180°のとき。つまり\(\overrightarrow{a} / / \overrightarrow{b}\)のとき。
たろぅはぁ…ベクトルの成分計算として考えれば、内積と大きさの関係から求めることができるのか。
ちなみに、「不等式の証明」で出てきた等号成立の\( a_1 b_2 = a_2 b_1\)は、\(\displaystyle \frac{a_1}{b_1} = \frac{a_2}{ b_2}\)と変形できます。だたし、以降は面倒なので\(a_i \neq 0\)、\(b_i \neq 0\)とします。
一方、「ベクトルを使った証明方法」で出てきた等号成立の\(\overrightarrow{a} / / \overrightarrow{b}\)は、平行条件から\(\overrightarrow{a} = k\overrightarrow{b}\)なので、\( (a_1, a_2)=k(b_1, b_2)\)。\(k\)を消去すると\(\displaystyle \frac{a_1}{b_1} = \frac{a_2}{ b_2}\)となります。
n個のコーシーシュワルツの不等式を証明
こちらの証明はとても面白いです。
n個のコーシーシュワルツ、つまり先ほどの
・一般的に\(a_i\)、\(b_i\)\( (i=1 , 2 , \cdots , n) \)について、以下の不等式が成り立つ。
\( (a_1^2+a_2^2+ \cdots +a_n^2)(b_1^2+b_2^2 +\cdots +b_n^2) \geq (a_1 b_1 + a_2 b_2+ \cdots + a_n b_n)^2 \)
こちらの証明方法です。
せんせ早速証明していきましょう！
（証明）
突然ですが、\(x\)についての二次式を考えます。
それは、\((a_i x-b_i)^2\)を足し合わせた、こんな形です。
\( (a_1 x – b_1)^2+(a_2 x – b_2)^2+ \cdots + (a_n x – b_n)^2 \) …②
この式は\(x\)の一次式を二乗して足しているので、\(a_i\)、\(b_i\)、\(x\)がどんな値でも、実数である限り0以上になります。
つまり、
\( (a_1 x – b_1)^2+(a_2 x – b_2)^2+ \cdots + (a_n x – b_n)^2 \geq 0 \)が成り立ちます。
ここで、左辺を展開して、\(x\)の降べきの順にまとめます。
\( (a_1^2+a_2^2 + \cdots + a_n^2)x^2-2(a_1 b_1 + a_2 b_2+\cdots+a_n b_n)x+(b_1^2+b_2^2 + \cdots + b_n^2) \geq 0 \)が成り立ちます。
左辺は「二次関数の形をしている」と見ると、「（下に凸の放物線を表す二次関数）\(\geq 0\)」が成り立っているとみなせます。
ということは、判別式\(D/4\)について、
\( D/4 \leq 0\)が成り立つ、ということです。
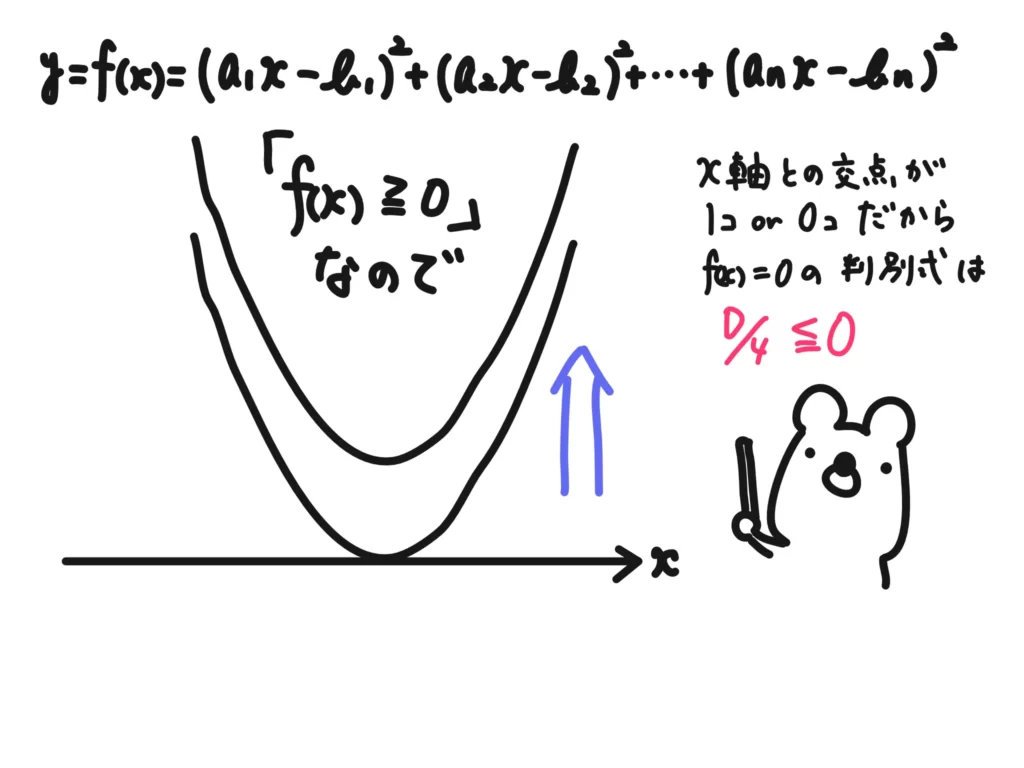
よって、
\( (a_1 b_1 + a_2 b_2+\cdots+a_n b_n)^2-(a_1^2+a_2^2 + \cdots + a_n^2)(b_1^2+b_2^2 + \cdots + b_n^2) \leq 0 \)
\( (a_1^2+a_2^2+ \cdots +a_n^2)(b_1^2+b_2^2 +\cdots +b_n^2) \geq (a_1 b_1 + a_2 b_2+ \cdots + a_n b_n)^2 \)
等号成立は②の全ての\(a_ix-b_i\)について、\(a_ix-b_i=0\)のとき。つまり、各\(a_i \neq 0\)のとき\( \displaystyle \frac{b_1}{a_1}=\frac{b_2}{a_2}=\cdots=\frac{b_n}{a_n}\)で等号成立。（終）
せんせ１次式を二乗したものの和を考えて、２次関数のグラフに話を振ってやるのが面白いですよね。
まとめ
コーシーシュワルツの不等式を証明しました。
コーシーシュワルツの不等式の証明方法は面白いものも多く、また、この式自体も他の不等式の証明に使えたりもするので、テーマ性があって面白いですね。
あわせて読みたい
相関係数の求め方や範囲が-1≦r≦1になる理由って？
相関係数…ご存知でしょうか？ 高校数学で言えば、数学Iの「データの分析」で出てくるのですが、相関係数は、２つの変量の間にどのような関係があるか？を数値化したもの…
あわせて読みたい
面白くてオススメの数学本・マンガ
最近よく「オススメの数学の本はありますか？」という質問を受けます。 正直、あんまり本は読まないのですが、これまで読んできた中で「これは面白い！」というオススメ…
ちょっと一息
このブログで活躍してるクマのLINEスタンプもあります！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
