ベクトルの内積とは？【求め方や証明とイメージ】

2022年9月20日2025年7月6日

ベクトルの内積…。

「ベクトルの掛け算」に相当する計算ですが、なぜあんな計算をするのでしょうか？

たろぅ

えー…そういう風に決めたから？

この記事では、わかりそうでわからないベクトルの内積について、定義やなぜあんな計算をするのか、などの説明をしていきます。

デカ丸

内積は、あの定義だから便利なんですよ

内積とは？

はなこ

ふむふむ…なるほど…。深いわぁ…。

たろぅ

はなこさん、何読んでるの？

はなこ

たろう君…。

たろぅ

ん？

はなこ

「愛」の反対って…なんだと思う？

たろぅ

え…なに？いきなりその質問…。えーっと…「あいつ、ムカつくぜ！」とか？

はなこ

ふ…そこで会話文が出てくるところがアナタのレヴェルの低さなのよ…。
エリ・ヴィーゼル氏曰く、「愛の反対は憎しみではない。無関心」よ。
まぁ、私は教養のないアナタなんかに関心は無いですけどね。
さ、勉強しなきゃ。

たろぅ

（ボクに対して無関心だ…）

ということで（？）内積です。

ベクトルの和や差、実数倍なんかを勉強したら、やはり次に考えたくなるのは、

「積（掛け算）」

ですよね。

ただ、ベクトルは「大きさ」に加えて「向き」の要素を持ちます。

なので「掛け算」といっても、例えば単純に大きさ同士を掛けるのではあまり上手い定義の仕方とは言えません。「向き」の要素が考慮されないからです。

上のやりとりは意味のない茶番のような感じですが、実は内積の計算も

「２つのベクトルが同じ向きのときに内積の値が大きくなる」

「２つのベクトルが反対向きのときに内積の値はマイナス方向に大きくなる」

「２つのベクトルが無関係（お互いの向きの要素が無い）＝垂直だったら内積０」

という性質があります。この性質を知っていれば解きやすくなる問題もあります。

せんせ

ということで、内積の定義２パターンを押さえていきましょう。

定義１．図を使った内積の定義

図形的な性質を使った定義

\( \overrightarrow{a}\)と\( \overrightarrow{b}\)の成す角（\(0° \leq \theta \leq 180°\)）とすると、内積\( \overrightarrow{a} \cdot\overrightarrow{b}\)は次のように計算できる。

\(\overrightarrow{a} \cdot\overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}| \cos{\theta}\)

定義２．成分表示を使った内積の定義

成分表示を使った定義

\(\overrightarrow{a}=(a_1, a_2)\)と\( \overrightarrow{b}=(b_1, b_2)\)の内積\( \overrightarrow{a} \cdot\overrightarrow{b}\)は次のように計算できる。

\( \overrightarrow{a} \cdot\overrightarrow{b}=a_1 b_1 + a_2 b_2\)

内積の求め方については、上記の２つの計算方法を押さえておけばOKです。

図形的なアプローチと成分的なアプローチ…どちらも内積の定義として重要です。

おまけ．空間（３次元）における内積

空間における内積も定義は同じです。

図形的な性質を使った定義

\(\overrightarrow{a} \cdot\overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}| \cos{\theta}\)

成分表示を使った定義

\(\overrightarrow{a}=(a_1, a_2, a_3)\)と\( \overrightarrow{b}=(b_1, b_2, b_3)\)の内積\( \overrightarrow{a} \cdot\overrightarrow{b}\)は

\( \overrightarrow{a} \cdot\overrightarrow{b}=a_1 b_1 + a_2 b_2 + a_3 b_3\)

せんせ

実際には空間における成す角は求めることが難しいので、成す角が与えられていないと図形的な性質を使った定義での計算は難しいです。
成分表示は\(z\)成分が加わっただけなのでわかりやすいですね！

内積の図形的な意味って？

冒頭でも話をしましたが、内積はベクトルの掛け算なので、「向き」も考慮したいところです。

特に、内積の図形的な性質を使った定義に「向き」を考慮した計算イメージを持たせることができます！

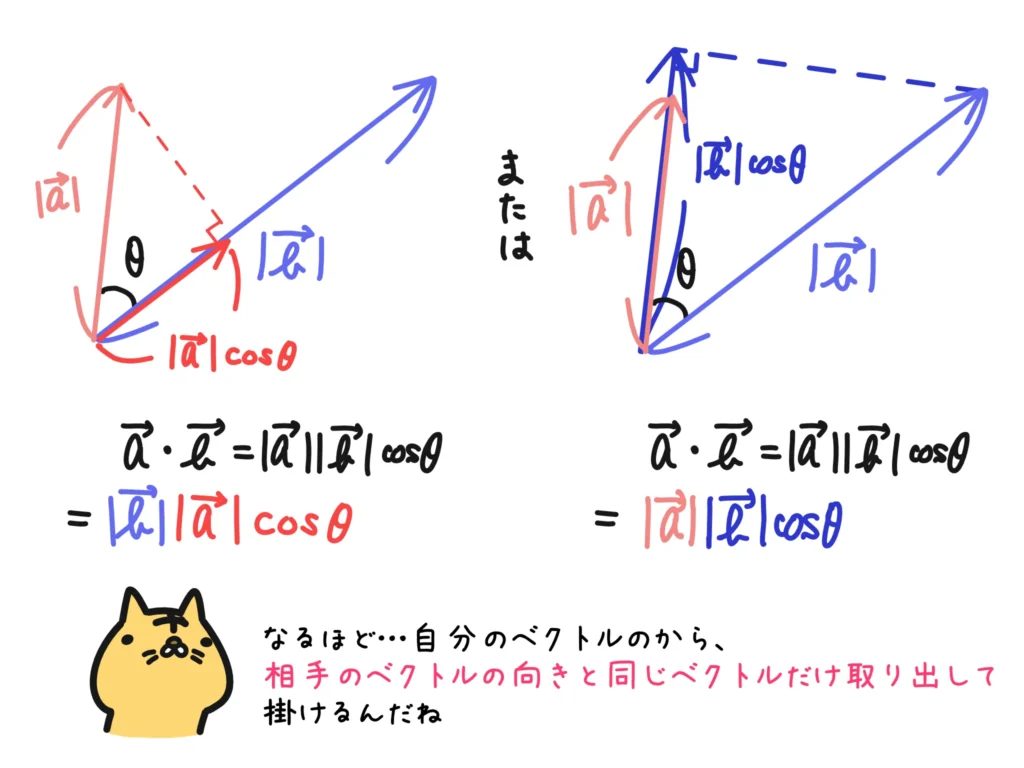
相手のベクトルに影を落とすように垂線を下ろして（正射影といいます）、その長さと相手のベクトルの長さを掛ける感じです。

要は自分のベクトルから相手のベクトルの向きと同じベクトルを分解して取り出して、その大きさを掛けているんですね。

あわせて読みたい

ベクトルの分解？一次結合？超重要な「ベクトルの一意性」とは？ベクトルは便利で重要な考え方ですが、苦手な人が多い分野でもあります。原因は「イメージ」と「その場での思考」が重要だからです。その状況に応じた対応って苦手…。…

\( | \overrightarrow{a} | \cos{\theta}\)や\( | \overrightarrow{b} | \cos{\theta}\)の図形的な意味がわかりにくい、という人はこちらの記事もあわせて読んでみてください。

あわせて読みたい

三角比とは？その「本質的な利点」をわかりやすく説明三角比…アレですよ、高校で習ったヤツ。 \( \sin \)、\( \cos \)、\( \tan \) やばい、拒否反応が…。わかりますよ。まぁ、これこそ高校数学で「なんでそんなもん考える…

せんせ

このように、内積は「自分がもつ相手方向の要素を掛ける」という「向き」を考慮した計算方法だ、ということがわかります。

内積の性質と証明

内積は、以下のようないくつかの性質があります。

性質①

\(-|\overrightarrow{a}||\overrightarrow{b}| \leq \overrightarrow{a} \cdot\overrightarrow{b} \leq |\overrightarrow{a}||\overrightarrow{b}|\)

これは、\(\overrightarrow{a} \cdot\overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}| \cos{\theta}\)で\( -1 \leq \cos{\theta} \leq 1\)だからですね。内積の最小値は大きさ同士を掛けたものにマイナスをつけたもの、最大値は大きさ同士を掛けたもの、になります。

性質②

\(\overrightarrow{a} \neq \overrightarrow{0}\)、\(\overrightarrow{b}\neq \overrightarrow{0}\)のとき、

\( \overrightarrow{a} \cdot\overrightarrow{b}=0 \Leftrightarrow \overrightarrow{a} \perp \overrightarrow{b} \)

ベクトルの垂直条件ですね。\(\cos{90°}=0\)なので、「内積＝０のとき垂直」だし「垂直のとき内積＝０」になります。（正確にはどちらのベクトルも\(\overrightarrow{0}\)でない、という条件が必要ですが）

「内積＝０のとき垂直」というのは図形の特徴として重要ですし、計算した結果「内積＝０」になるケースが結構あるので、内積の性質の中でも最重要事項です。

はなこ

反対向きの要素を持ったベクトル同士の内積の値は「ー（マイナス）」になるけど、垂直同士は互いに無関心（お互いの方向の要素を持っていない）だから「内積＝０」になるのね。

性質③

\( \overrightarrow{a} \cdot\overrightarrow{a} = |\overrightarrow{a}||\overrightarrow{a}| \cos{0°}= |a|^2\)

これも地味ですが、かなり重要です。自分自身との内積を計算すると大きさの二乗になる、という性質です。

つまり、内積と大きさの二乗は密接に関係していて、内積があれば大きさを求めることができるし、逆に大きさから内積を計算することもできます。

性質④

\( \overrightarrow{a} \cdot\overrightarrow{b}=\overrightarrow{b} \cdot \overrightarrow{a} \)
\( (k\overrightarrow{a}) \cdot\overrightarrow{b}=\overrightarrow{a} \cdot (k\overrightarrow{b})=k(\overrightarrow{a} \cdot\overrightarrow{b}) \)
\( \overrightarrow{a} \cdot (\overrightarrow{b}+\overrightarrow{c}) = \overrightarrow{a} \cdot\overrightarrow{b} +\overrightarrow{a} \cdot\overrightarrow{c}\)

交換法則、実数倍、分配法則が成り立ちます。要は、普通の積の要領で計算していい、ということです。

せんせ

慣れれば展開公式を使うようにどんどん内積の計算ができるようになります。