PR
このブログで使う数学(算数)の基本的な知識・技術

このブログは、主に高校以上の数学の勉強内容を通して「数学ってこういうのが役に立つんだ」という認識をしてもらって「意外と数学って楽しいかも」と思ってもらうのが目標です。

もちろん、中学校や小学校の勉強内容でも「考えることの楽しさ」を知ることができますし、実際に中学校や小学校で勉強する内容で記事も書いています。

ですが、基本的に高校以上の勉強内容で話を進めていくので話の中でサラッと「これってなんだったっけ?(小or中学校で習ったような…)」というようなものも出てくると思います。
そういう「あら?これってなんだったっけ?」という内容をまとめて、参照できるようにする、というのがこの記事です。簡単にポイント解説もしていきたいと思います。
もちろん、例え小学校で習うようなカンタンな内容でも、人間は忘れます。私も油断すると忘れます。
ですので、この記事で「ん?」と思った部分は遠慮なくこちらの記事を見て、アタマを刺激してください!
小学校で習う内容
分母・分子に同じ数をかける
高校生でも意外と苦手、結構厄介な「分数計算」。
分母・分子に同じ数をかける、という意味でいくつかの操作を押さえておきます。
① 通分計算
 せんせ
せんせそもそも通分は「単位合わせ」です。「1m足す1cmは?」と言われて「2m」とか「2cm」と計算できないのと一緒ですね。
例1.\(\displaystyle \frac{1}{2} + \frac{1}{3} =\frac{1 \cdot 3}{2 \cdot 3} + \frac{1 \cdot 2}{3 \cdot 2}\)(←分母・分子に同じモノを掛けることができる。)
\( = \displaystyle \frac{3 + 2}{6} = \frac{5}{6}\)
例2.\(\displaystyle \frac{1}{6} + \frac{1}{4} =\frac{1 \cdot 2}{6 \cdot 2} + \frac{1 \cdot 3}{4 \cdot 3}\)(←最小公倍数になるように分母・分子に同じものを掛ける。「6」は2で割ったものを更に3で割る、「4」は2で割ったものを更に2で割る、と考えれば、6と4はそれぞれ更に2と3で割れば単位が合う。)
\( = \displaystyle \frac{2 + 3}{12} = \frac{5}{12}\)
② 約分
約分も分母分子に同じものをかける、という意味では操作は同じです。
例1.\( \displaystyle \frac{2}{4} = \frac{2 \cdot \frac{1}{2}}{4 \cdot \frac{1}{2}}=\frac{1}{2} \)
\( \displaystyle \frac{2}{4} = \frac{2 \div 2}{4 \div 2}=\frac{1}{2} \)というイメージかもしれませんが、2で割ることと\(\displaystyle \frac{1}{2}\)を掛けることは同じことですね。
③ 分数の中の分数を解消する
これは小学校レベルの話ではないですが、「分数を分数で割る」という話でいえば小学生レベルと言えるかもしれません。



「分数で割る」というときに、こういう教わり方をすることはあまりないかもしれません。
小学校で「分数で割る」ときには「逆数を掛けるんだよ」というくらいしか習わないかもしれません。「なぜ逆数を掛けるの?」という疑問もあるかもしれませんが、この「分数の中の分数を解消する」という話でも説明ができます。
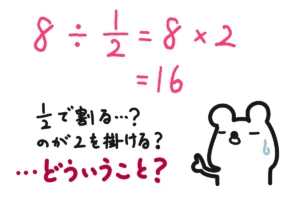
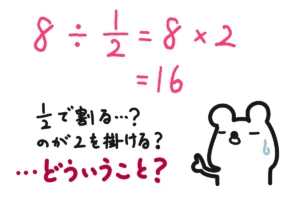



前提として、\( \displaystyle a \div b = \frac{a}{b} \)となることは押さえておいてください。
例1.\( \displaystyle 5 \div \frac{1}{4}\)の計算について。
\( \displaystyle 5 \div \frac{1}{4} = 5 \times \frac{4}{1} = 20\)という形で、分数で割るときは逆数を掛ける、という計算でも構いません。しかし、先ほどの\( \displaystyle a \div b = \frac{a}{b} \)となる計算を使うと次のようになります。
\( \displaystyle 5 \div \frac{1}{4} = \frac{5}{\frac{1}{4}} =\frac{5 \cdot 4}{\frac{1}{4} \cdot 4} = \frac{20}{1} = 20\)
分数の中の分数を解消するために、分母分子に同じ4を掛ければ、分母の\( \displaystyle \frac{1}{4} \)を解消することができます。結果、計算結果は20になりますね。
例2.\( \displaystyle 5 \div \frac{2}{3}\)の計算について。
これも先ほどと同じで、\( \displaystyle 5 \div \frac{2}{3} = 5 \times \frac{3}{2} = \frac{15}{2}\)と計算することもできますが、
\( \displaystyle 5 \div \frac{2}{3} = \frac{5}{\frac{2}{3}} =\frac{5 \cdot 3}{\frac{2}{3} \cdot 3} = \frac{15}{2}\)
というふうに、分数の中の分数を解消する形で計算ができます。
例3.小学校の範囲からは完全に逸脱してしまいますが、次のような式を整理するのは高校生でも苦手な人が多いです。
\( \displaystyle y = \frac{2}{x+ \frac{1}{x}}\)
「\(x>0\) のとき、最大値を求めなさい」なんて問題を出したくなる関数ですが、とりあえず「分数の中の分数\(\displaystyle \frac{1}{x}\)を解消したいな」というときは、
\( \displaystyle y = \frac{2}{x+ \frac{1}{x}} = \frac{2 \cdot x}{(x+ \frac{1}{x}) \cdot x} = \frac{2x}{x^2+1}\)
という感じで整理します。



この、分母分子に同じものを掛けたときに、特に今回で言えば「分母の\( \displaystyle x+ \frac{1}{x}\)に\(x\)を掛けたときに\( (x+ \frac{1}{x}) \cdot x\)となる、というのが苦手な人が多いですね。
中学校で習う内容
不等式の両辺、逆数をとると?
不等式自体は中学校で習うのですが「不等式の両辺逆数をとるとどうなるのか?」という、ツッコんだ内容までは習うのかわかりません…。
が、これも高校生でもアヤシイ生徒がいるので、どうなるか押さえておきます。



パターン別にわかれるので、結構厄介です…。
①両辺が同符号の場合
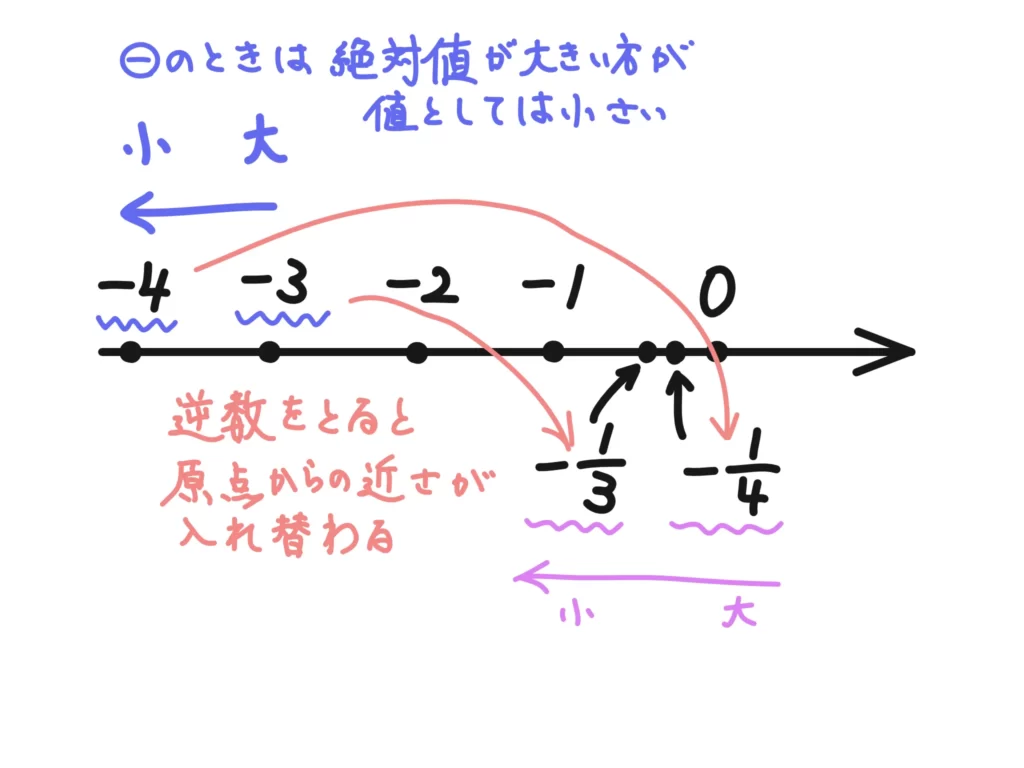
両辺逆数をとったときに、不等号の向きが入れ替わります。
簡単に説明すると、数が大きくなればなるほど逆数をとったときに(大きい)→ \( \displaystyle \frac{1}{(大きい)} \)となることで、結果として小さな数となりますよね?分母が大きくなるので。
つまり、基本的に\((小さい) \le (大きい)\)→\( \frac{1}{(小さい)} \ge \frac{1}{(大きい)}\)というイメージをもってもらえればいいです。
例1.\(\displaystyle 3 \le 5 \rightarrow \frac{1}{3} \ge \frac{1}{5} \)
例2.\(\displaystyle -4 \le (-3) \rightarrow -\frac{1}{4} \ge (-\frac{1}{3}) \)
マイナスの場合はちょっと分かりにくいですが、こんな感じですね。

②両辺が異符号の場合
片方がプラスで片方がマイナスの場合です。これは逆数をとっても不等号の向きは変わりません。プラスとマイナスの時点で大小関係がはっきりしているからです。
例.\( -3 \le 2 \)のとき、逆数をとっても\( – \frac{1}{3} \le \frac{1}{2} \)となり、不等号の向きは変わりません。
両辺が異符号のケースはあまり見かけないですが、意味を考えれば当たり前といえば当たり前です。
内項の積=外項の積
比例式を扱うときの計算方法です。結論から書くと、
\( a : b = c : d\)のとき「=」を挟んで、内側の項を掛けた\(b \cdot c \)と外側の項を掛けた\(a \cdot d \)は等しくなる、という計算方法です。
\( a : b = c : d \Leftrightarrow b \cdot c = a \cdot d \)
例1.\( 2 : 3 = x : 5 \Leftrightarrow 3 \cdot x = 5 \cdot 2 \)
\( x = \frac{10}{3} \)
なぜこうなるのか説明してもいいんですが、上記の計算ができるんだ、くらいの理解でもいいと思います。
ということで、比例式に関わる重要な性質について押さえておく、程度に留めておきます。次の性質は重要ですので、ぜひ覚えておいてください。
① 比例式は、「:」を挟んだ右と左に同じものを掛けて良い。
\( a : b \Leftrightarrow a \cdot k : b \cdot k \)
② 比例式と分数は同じ。これは結構重要。さっきの「同じものを掛けて良い」とか「連比」とか「三角比」とか、分数として扱っているものの正体が実は比だった、というのはよくある。
\( a : b \Leftrightarrow \displaystyle \frac{a}{b} or \frac{b}{a} \)
①の\( a : b \Leftrightarrow a \cdot k : b \cdot k \)も、\(\displaystyle \frac{a}{b} = \frac{a \cdot k}{b \cdot k} \)が成り立つ、と思えば自然に分数に対応させることができる。
「内項の積=外項の積」の説明はコチラ
先ほどの性質ベースで話をしていきましょう。
① 比例式は、「:」を挟んだ右と左に同じものをかけて良い。
\( a : b \Leftrightarrow a \cdot k : b \cdot k \)
① 比例式は、「:」を挟んだ右と左に同じものをかけて良い。
\( a : b \Leftrightarrow a \cdot k : b \cdot k \)
\(a : b = c : d\)が成り立つとき、わかりやすいのが「:」を挟んだ左右どちらかを1に揃えて比較、という方法でしょう。
\(a : b = \displaystyle \frac{a}{b} : 1\)(←\( \displaystyle \frac{1}{b}\)を掛けた)、\(c : d = \displaystyle \frac{c}{d} : 1\)(←\( \displaystyle \frac{1}{d}\)を掛けた)なので、
\( \displaystyle \frac{a}{b} : 1 = \displaystyle \frac{c}{d} : 1\) が成り立つ。
ということで、\( \displaystyle \frac{a}{b} \)と\( \displaystyle \frac{c}{d} \)を比較して、
\( \displaystyle \frac{a}{b} = \displaystyle \frac{c}{d} \)
よって、\( b \cdot c = a \cdot d \)。
② 比例式と分数は同じ。
\( a : b \Leftrightarrow \displaystyle \frac{a}{b} or \frac{b}{a} \)
\(a : b = c : d\)が成り立つとき、\(a:b \Leftrightarrow \displaystyle \frac{a}{b}\)、\(c:d \Leftrightarrow \displaystyle \frac{c}{d}\)なので、
\( \displaystyle \frac{a}{b} = \displaystyle \frac{c}{d} \)
よって、\( b \cdot c = a \cdot d \)。



特に(分数)=(比)という考え方は押さえておいた方がいいです。
まとめ
数学や算数に関する知識・技術を随時更新していきます!






