PR
標本平均や標本比率の分布と正規分布【流すところを丁寧に】
この記事では標本平均や標本比率の分布と正規分布の関係について説明していきます。
せんせ今回は軽めに説明していきます。
目次
標本平均の分布
ある教科書ではいきなりこんな感じで書かれています。
標本平均\(\bar{X}\)の分布について、次の性質があることが知られている。
…標本平均\(\bar{X}\)は\(n\)が大きいとき、近似的に正規分布\(\displaystyle N \left( \mu ,\frac{\sigma ^2}{n} \right)\)に従うとみなすことができる。
たろぅ…？標本平均の分布？
この記事で説明する標本平均の分布と標本比率の分布は、あまり丁寧に触れられない部分ですが、最初勉強するときにイメージが掴みにくいかな、と思います。
せんせこのあとの「推定」のときとかにわからなくならなければいいんですが…。
「標本平均の分布」のイメージを掴んでもらえたら、と思います。
この標本平均の分布、というのはいわゆる中心極限定理のことです。
中心極限定理
母平均\(\mu\)、母分散\(\sigma^2\)である母集団（基本的に分布の形は問わない）から標本の大きさ\(n\)の標本を取って標本平均を計算すると、その標本平均は正規分布\(\displaystyle N \left( \mu ,\frac{\sigma ^2}{n} \right)\)に従います。
「標本平均の分布が正規分布に従う」というのが最初はイメージしにくいと思います。
たろぅん…？標本平均って、その標本の平均でしょ？平均が分布に従うってどゆこと？
例えば、サイコロを1回投げたときの分布を考えると少しイメージしやすいです。
せんせサイコロを１回投げたときの分布は次のようになります。
| \(X\) | 1 | 2 | 3 | 4 | 5 | 6 | 計 |
| \(P(X)\) | \(\displaystyle \frac{1}{6}\) | \(\displaystyle \frac{1}{6}\) | \(\displaystyle \frac{1}{6}\) | \(\displaystyle \frac{1}{6}\) | \(\displaystyle \frac{1}{6}\) | \(\displaystyle \frac{1}{6}\) | 1 |
このとき、実際にサイコロの目は１つに決まりますよね？
ですが、サイコロの目は「上記の分布に従う」と言います。
話を標本に戻すと、標本をとってきたときに、その平均（標本平均）は元の母集団の母平均や母分散、標本の大きさによって変わります。
実際にその標本に対する標本平均は１つに決まりますが、その値は様々な値をとる可能性があります。
この標本平均を変数と見たときに従う分布が、正規分布\(\displaystyle N \left( \mu ,\frac{\sigma ^2}{n} \right)\)だ、ということですね。
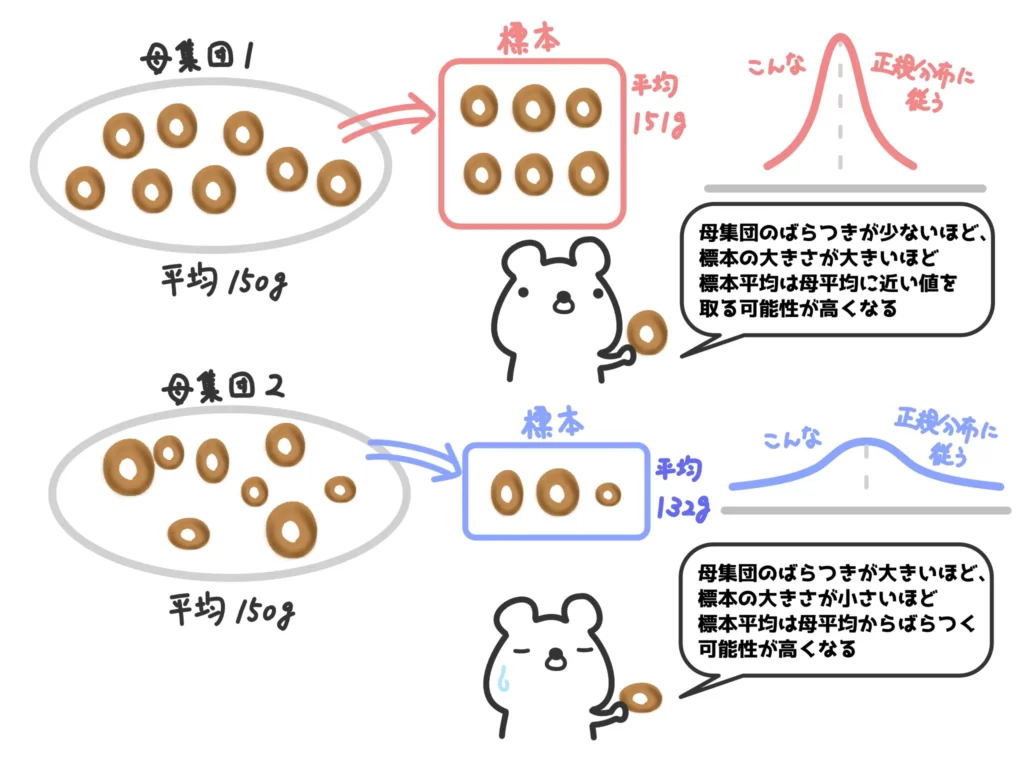
せんせ例えば、「母分散\(\sigma ^2\)が小さい」「標本の大きさ\(n\)が大きい」とこの正規分布の分散は小さくなります。つまり、標本平均の取りうる値が母平均\(\mu\)の周りに集中する、ということですね。
これが\(n\)が大きいときに標本平均が母平均\(\mu\)の周りに集中する、という中心極限定理が主張していることです。
数学をモチーフにしたオシャレなオリジナルグッズも販売中です！おかげさまで好評頂いてます！
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ！
標本比率の分布
母集団のうち、ある特性を持つものの比率を母比率、標本のうち、ある特性を持つものの比率を標本比率、といいます。
たろぅ（ある特性…？）
「ある特性」というとザックリしていますが、例えばこんな感じです。
例１．昨日の特番「楽しいクマの生態！」を見たかどうかを１００人に街頭アンケートしてみた。
例２．鮭５００匹を捕まえて、イクラが入っているかどうかを調べてみた。
要は「Yesかそうでないか？」で判断できる特徴、と思ってもらえればOKです。
せんせ例でも分かる通り、母比率や標本比率はアンケートや調査などで使うことが多いです。
「Yesかそうでないか？」ということは、この母比率や標本比率は二項分布の話なんですね。
ということで、最終的に流れとしては、
「二項分布」→「正規分布に近似」→「標準化して標準正規分布表から確率を求める」
という作業になります。
せんせそれでは、標本比率が実際にどんな分布に従うか、説明していきましょう。
特性Aを持つ、という母比率が\(p\)であるとする。
大きさ\(n\)の標本を取ってきたときに、特性Aをもつ個数を確率変数\(X\)で表す。
二項分布で説明したときと同じように、
\(X\)は1個目の標本から\(n\)個目の標本までのそれぞれの確率変数\(X_i\)（\(i=0, 1, 2, \cdots, n\)、それぞれの\(X_i\)が取りうる値は0か1です。）を足して作ることができる、
という点がポイントです。つまり、
\(X=X_1+X_2+\cdots+X_n\)（\(n\)個の標本がそれぞれ特徴Aをもつかかどうか？の和）で表現できます。
これは、「１回の試行（\(X_i\)）が1となる確率\(p\)（母比率）の試行を、\(n\)回繰り返した」ことと同じなので、二項分布\(B(n,p)\)に従います。
せんせあとは、二項分布→正規分布への近似と変数変換です。
こちらで説明していますが、
二項分布\(B(n,p)\)は試行回数\(n\)が大きければ正規分布\(N(np,np(1-p))\)に近似することができます。
ただ、これはあくまで「\(n\)個の標本のうち特性Aをもつものの個数」が従う分布なので、「標本比率」が従う分布ではありません。
標本比率\(R\)は
\(\displaystyle R = \frac{X}{n}=\frac{X_1+X_2+\cdots+X_n}{n}\)
\(\displaystyle N \left( \frac{np}{n},\frac{np(1-p)}{n^2} \right)\)つまり\(\displaystyle N \left( p,\frac{p(1-p)}{n} \right)\)に従います。
特性Aをもつ母比率\(p\)の母集団から標本の大きさ\(n\)の標本を無作為抽出すると、その標本比率\(R\)は\(n\)が大きいときに正規分布\(\displaystyle N \left( p,\frac{p(1-p)}{n} \right)\)に従うとみなせる。
例．不良品が全体の10％含まれる大量の製品から、大きさ100の標本を無作為抽出するとき、不良品の標本比率\(R\)について。
(1) \(R\)はどのような正規分布に従うとみなせるか？
(2) \(0.04 \leq R \leq 0.16\)となる確率を求めよ。
（解）
(1)\(R\)は正規分布\(\displaystyle N \left( 0.1 , \frac{0.1(1-0.1)}{100} \right)\)つまり
\(\displaystyle N \left( 0.1 , 0.03^2 \right)\)に従う。…（答）
※コツ
分散\(\displaystyle \frac{0.1(1-0.1)}{100}\)の計算をするとき、後々のことを考えて標準偏差ベースで計算しておくとイイ感じです。
つまり、ガチンコで計算すれば\(\displaystyle \frac{0.1 \times 0.9)}{100} = 0.0009\)になりますが、(分散)＝\( (標準偏差)^2\)なので、あえて２乗ベースで計算していきます。
\(\displaystyle \frac{0.1 \times 0.9}{100} = \frac{10^{-1} \times 3^2 \times 10^{-1}}{10^2} = 3^2 \times 10^{-4} = (3 \times 10^{-2} )^2 \)
(2) (1)で\(R\)は期待値\(0.1\)、標準偏差\(0.03\)の正規分布に従う、ということがわかったので、これを使って標準化していきます。
\(\displaystyle Z = \frac{R-0.1}{0.03}\)
とすれば、\(Z\)は標準正規分布に従います。
\(R = 0.04\)のとき\(Z = -2\)、\(R = 0.16\)のとき\(Z = 2\)となるので、標準正規分布表を使って確率を求めると、0.9544…（答）
まとめ
サクッと説明するつもりが…意外とボリュームタップリになってしまいました。
せんせ教科書ではサラッと流すところですが、実はちゃんと理解しようと思ったらこのくらいしっかりやらないといけない、ということですね汗。
ちょっと一息
数学をモチーフにしたオシャレなオリジナルグッズも販売中です！おかげさまで好評頂いてます！
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ！
また、このブログで活躍してるクマのLINEスタンプも販売しています！ぜひ一度見てみてください！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
