二項分布と正規分布の関係【例を使ってわかりやすく解説】

2023年8月9日

統計において、二項分布と正規分布はどちらも基本的な確率分布ですが、二つの間には深い関係があります。

この記事では、二項分布と正規分布の関係について説明していきます。

二項分布と正規分布の関係

せんせ

…はい、じゃあ計算しといてください。

たろぅ

…いや、無理ですよ。この確率は面倒です。

せんせ

自分で言い出したんじゃないですか、計算してくださいよ。

はなこ

なにやってるんですか？

たろぅ

いや、さっきカタン（ボードゲーム。実際にあります。面白い、オススメ。）やってたんだけど。今回盗賊（２つのサイコロの目の和が７）があんまり…１０回しか出なかったんだよね。で、「今の８０回のサイコロ投げのうち、盗賊が１０回以下しか出ない確率ってどのくらいだろう？」って言ったら、計算しろってこのオニ…先生が言うんだ。

せんせ

…

最近個人的にハマってるオススメのボードゲーム「カタン」が出てきましたが、ボードゲームのルールは抜きにして、要はこういうことです。

（問）サイコロを２個投げたときの目の和を考える。２個のサイコロを８０回投げたとき、目の和が７である回数が１０回以下である確率を求めよ。

ちょっと考えたらすごく計算が大変だ、ということはわかると思います。

ちなみに、反復試行の確率で計算しないといけません。一回のサイコロ投げで目の和が７になる確率は\(\displaystyle \frac{6}{36}=\frac{1}{6}\)で、８０回中１０回以下（１０回、９回、…、１回、０回）の確率を全て足さないといけないので、求める確率は

\(\displaystyle _{80}C_{10} \left( \frac{1}{6} \right)^{10}\left( \frac{5}{6} \right)^{70}+ _{80}C_{9} \left( \frac{1}{6} \right)^{9}\left( \frac{5}{6} \right)^{71}+\cdots + _{80}C_{0} \left( \frac{1}{6} \right)^{0}\left( \frac{5}{6} \right)^{80}\)

…太郎くんが「オニ」というのもわかります。

そこで正規分布の出番です！二項分布は試行回数が多ければ、正規分布とみなせるという性質があります。

せんせ

ということで、正規分布とみなすことで、ガチンコ計算した値とほぼ近い値を求めることができます！

二項分布と正規分布の関係

二項分布\(B(n,p)\)は試行回数\(n\)が大きければ正規分布\(N(np,np(1-p))\)に近似することができる。

※補足：二項分布\(B(n,p)\)の期待値は\(np\)、分散は\(np(1-p)\)になります。よって、自然と正規分布を決定する２つの要素「平均（期待値）」と「分散」はそれぞれ、「\(np\)」と「\(np(1-p)\)」になります。

【どうでもいい話】

太郎くんが話してたカタン…めちゃくちゃ面白いですよ。

３〜４人で遊ぶボードゲームで、２個のサイコロを順番に投げて資源を獲得！街や道を発展させてポイントを競うゲームです！

話に出てきたオジャマ虫「盗賊」や、他のプレイヤーとの取引が醍醐味！運以外の駆け引き・戦略要素も大きく、公式競技として大会も行われるほど。

たろぅ

興味があったらやってみてね。

リンク

例題を使って二項分布で表される分布の確率を求めてみよう

せんせ

先ほどの例を使って、実際に確率を求めてみましょう！

流れとしては、

「二項分布」→「正規分布に近似」→「標準化して標準正規分布表から確率を求める」

となります。正規分布から標準化して標準正規分布表を読む作業はこちらを参考にしてください。

あわせて読みたい

標準正規分布とは【正規分布との関係と標準正規分布表の見方を丁寧に説明】こちらの記事で、世の中の現象は「二項分布」や「正規分布」と見なせるものが多い、という話をしました。ですが、「二項分布」や「正規分布」はそのままでは計算しづら…

（解答）

今回は、試行回数が80、目の和が７になる確率\(\displaystyle \frac{1}{6}\)なので、二項分布\(\displaystyle B\left(80,\frac{1}{6}\right)\)に従います。

よって、正規分布\(\displaystyle N\left(80 \times \frac{1}{6},80 \times \frac{1}{6} \times\frac{5}{6} \right)\)つまり正規分布\(\displaystyle N\left(\frac{40}{3},\frac{100}{9} \right)\)に従う、とみなせます。

このとき、１０回以下である確率、

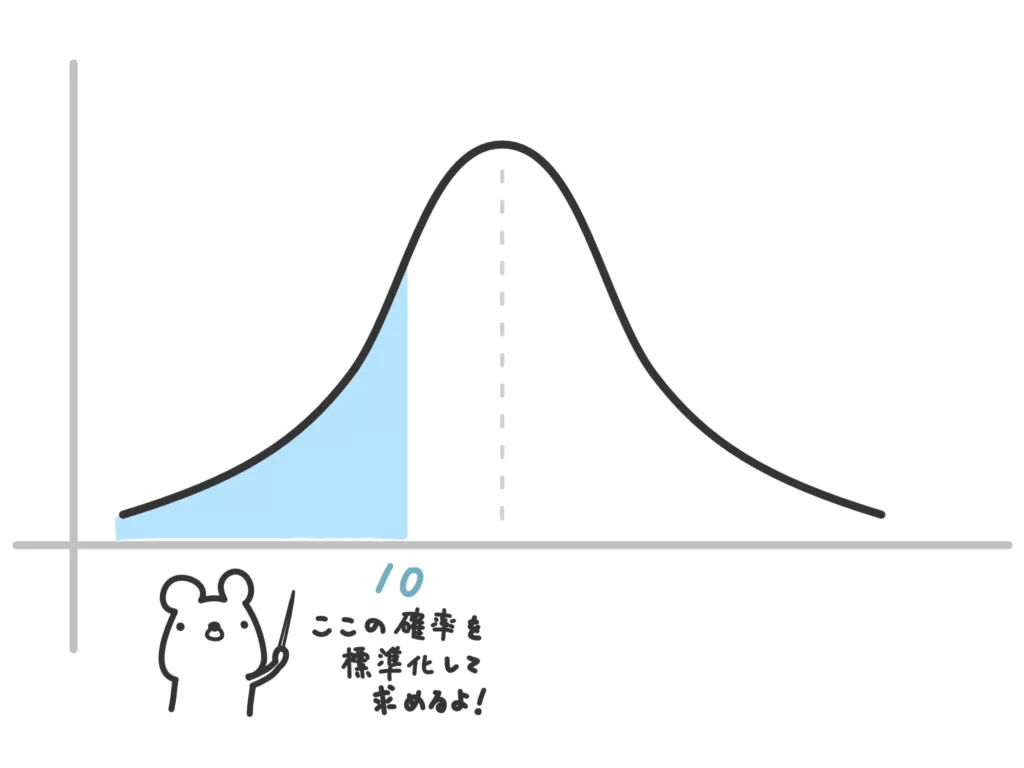
この部分の確率を求めていきます。

これを標準化すると、

\(\displaystyle Z=\frac{10-\frac{40}{3}}{\sqrt{\frac{100}{9}}} = -1\)

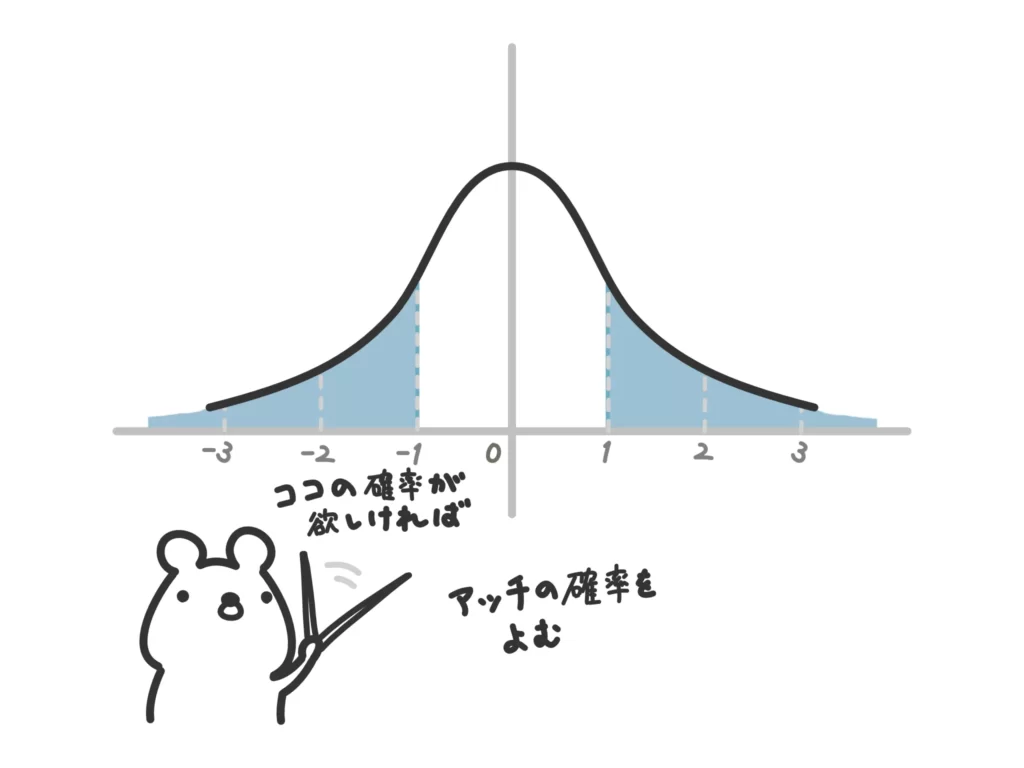
つまり、標準正規分布で\(Z \leq -1\)の確率を求めればよいのですが、標準正規分布表は\(Z \geq 0\)の確率しか与えられないので、対称性を利用して\(Z \geq 1\)を読みます。

	.00	…	.05	…	.09
0.0	0.5000	…	0.4801	…	0.4641
0.1	0.4602	…	0.4404	…	0.4247
…	…	…	…	…	…
0.8	0.2119	…	0.1977	…	0.0823
0.9	0.1841	…	0.1711	…	0.0681
1.0	0.1587	…	0.1469	…	0.0559
…	…	…	…	…	…
3.0	0.0013	…	0.0011	…	0.0010