PR
比や割合はなぜ分数で計算する!?その考え方って?

小学校で習う「比」…。
これ、実は高校生でも意外とわかっていない生徒が多いです。
日常生活でも使う基本的な考え方なのですが、それまで具体的な「値」を扱っていたのに対し、初めて少し抽象的な考え方が必要になってきます。
この記事では、小学生でもわかりやすく、高校生でも比の計算を上手く使えるように、徹底的に比や割合について解説をしていきます!
比や割合って?そもそも何?
調理実習で…。
 はなこ
はなこしょっぺぇ!この味噌汁しょっぺぇわ!!



おぉ…素の花子さん…。ちなみにその味噌汁は僕が作ったんだけど…。



どんだけ味噌入れたんじゃい!しょっぱすぎるわ!!



えー…このプリントに書いてあるレシピ通りに入れたけどなぁ…。ほら、「大さじ6杯」って書いてある。



これは「4人前」のレシピでしょうが!うちの班は今日2人休んで、あんたと私だけだから「水は半分でいいよ」って言ったけど、味噌も半分にせんかい!!



なるほど。



作り直し!!



…はい。
こんなのは「比」の話ですね。
比は「これを○とみなしたときに、こっちは△という値で表せる」という考え方で、少し抽象的な考え方になります。
今回の例で言うと、「これ」=「4(人前)」に対して「こっち」=「6(味噌大さじ)」という比になります。つまり、
(人数):(味噌)=\(4 : 6 \)
ですね。これが比の考え方と表し方になります。ちなみに、「:」の前にある値を前項、後ろにある値を後項といいます。
「具体的に何gって言ってくれた方がわかりやすい!」と思うかもしれませんが、なぜこんなわかりにくいことをするのか?というと、「比の考え方さえ掴めれば、応用が効きやすく、どんな状況にも対応しやすいから」です。
この辺りを説明していきましょう!
比の性質と計算
比の性質として、前項と後項に同じ値を掛けたり、同じ値で割ったりしても比としては同じ、というものがあります。比は割合なので、同じだけ掛けたり(引き伸ばしたり)、同じだけ割ったり(縮めたり)しても、割合は変わらないからです。
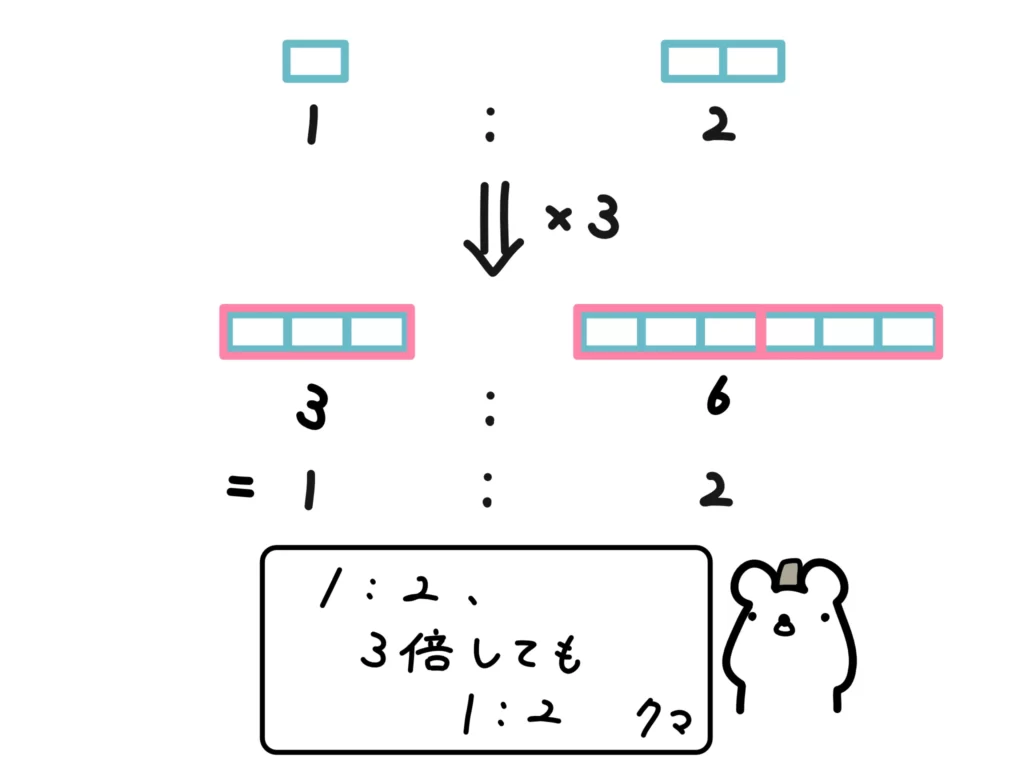

ちなみに、同じ値を「足したり」「引いたり」してはいけません。比が崩れます。
これは、例えば「100に対する+1」と「1に対する+1」では、同じ+1でもそれぞれの値に対する割合が違うからです。


さてそれでは、先ほどの「比の考え方さえ掴めれば、応用が効きやすく、どんな状況にも対応しやすいから」という点について説明していきましょう。
例えば、さっきの味噌の例で言うと、本来、
(人数):(味噌)=\(4 : 6 \)
なのですが、この人数が2人になってしまったということは、人数を\(\div 2\)すれば2人になりますね。つまり、味噌も\(\div 2\)してやればいいのです。
(人数):(味噌)=\(4 : 6 = (4 \div 2) : ( 6 \div 2) = 2 : 3 \)
味噌は大さじ3でよかった、ということになります。こういう計算が機械的にすぐにできるのが比の強みです。
これだけでは、少しありがたみがわかりにくいですが、例えば5人班であった、としましょう。このとき 、5人前の味噌の量を2つのアプローチで計算してみましょう。
- 人数「4」に色々掛けたり割ったりして「5」を作る。
- 人数「4」をいったん「1」にしておく。そうすると「5」が作りやすい。(5倍すればよい)



はっきり言って計算上はどちらも同じなのですが、比の計算に対していくつかの考え方を説明したいので、違うアプローチとします。
①人数「4」に色々掛けたり割ったりして「5」を作る
比の考え方や計算に慣れている人は、こちらがサッと計算できていいと思います。
最終的には分数の掛け算で計算するのですが、「この分数を掛けて計算すればいい」いう感覚になるまで慣れて欲しいです。



では計算していきましょう。
人数「4」に上手いこと値を掛けたり割ったりして、「5」を作っていきます。結論から言うと、
(人数):(味噌)=\(\displaystyle 4 : 6 = (4 \times 5 \div 4) : ( 6 \times 5 \div 4) = 5 : \frac{15}{2} = 5 : 7.5 \)
となるので、\(\times 5 \div 4\)すればいい、ということになります。
5人前の味噌汁は、味噌大さじ7.5杯だ、とすぐにわかります。
ですが、この計算方法は正直面倒なので、普通は分数を使います。
\(\displaystyle \div 4 = \times \frac{1}{4}\)なので、割り算は分数の掛け算として計算ができます。これを利用して「掛けたり割ったりして5を作る」というのを「分数の掛け算で5を作る」という計算方法に統一します。
つまり、
(人数):(味噌)=\(\displaystyle 4 : 6 = (4 \times \frac{5}{4}) : ( 6 \times \frac{5}{4}) = 5 : \frac{15}{2} = 5 : 7.5 \)
という感じで、\(\displaystyle \times \frac{5}{4}\)で一発で計算していきます。
実践的には「比の計算は分数の掛け算で行う」という感覚が重要です。これは高校生になってもよく使います。(これができない高校生が結構多いです。)
②いったん「1」人前の味噌を出しておく
こちらも結論としては先ほどの計算と同じなのですが、重要なのは「1」に対する比にしておけば、その後の計算がしやすい、という点です。



それではこちらのアプローチでも計算していきましょう。
(人数):(味噌)=\(\displaystyle 4 : 6\)
これを一番簡単な整数比に直すには、\(\div 2\)してあげればOKです。
(人数):(味噌)=\(\displaystyle (4 \div 2) : (6 \div 2) = 2 : 3\)
ですが、これにあまり数学的な意味はありません。
今回のアプローチのように、さらに\(\div 2\)をする(あるいは最初から\(\div 4\)をする)ことで、単位人数あたり(つまり「1」人あたり)の味噌の量を出しておきます。
(人数):(味噌)=\(\displaystyle (2 \div 2) : (3 \div 2) = (4 \div 4) : (6 \div 4) = 1 : \frac{3}{2} = 1: 1.5\)
この、「単位人数1人あたりの味噌の量1.5」を出しておくと、あとにどのような人数が来ても計算が楽チンです!
例えば「5人」と言われれば、5倍すればいいですよね?
\(1.5 \times 5 = 7.5\)
クラス全員「35人」分と言われれば、35倍すればOKです。
\(1.5 \times 35 = 52.5\)
つまり「1」に対していくらになるか?を出しておけば、たとえその値がキリが悪い値でも、数学的に使いやすいということになります。



だからまぁ、キリが悪くても「1人前のレシピ」の方が数学的には使いやすいです。実際には「2人前」とか「4人前」とかの方が需要が高いでしょうから、その人数分のレシピが多い気がします。このあたりは数学と現実のギャップですよね。
この「1に対していくらになるか?それをあらかじめ計算しておこう!」という考え方は、高校数学の「三角比」や「ベクトル(単位ベクトル)」でも重要な考え方になります。



同じように「1に対していくらになるか?」というアプローチで三角比の解説もしています。高校で習うけど、よく意味のわからない三角比も、わかりやすく解説しています!

比の計算の応用「割引計算」



やったー!購買が閉まるギリギリに行ったら、サンドイッチが3割引だったぞー!



よかったね。元の値段はいくらだったの?



350円だったよー。



じゃあ3割引でいくら?



…ちょっと待って。(早く食べないと昼休み終わっちゃうよ…)



そのサンドイッチ代350円、さっき「お金足りないから貸して!」って借りてったやつよね?割引分は今返してよね。



…はい。(シビアだな…明日まとめて返すってさっき言ったのに…)
これ、あるあるシチュエーションですね。「割引した後の値段がいくらか?」というやつです。これも実は比の計算で一発です。
今回、花子さんは「割引分」を返して欲しいので、3割は
\( 350 \times 0.3 = 105\)もしくは、\(\displaystyle 350 \times \frac{3}{10} = 105\)
で計算できます。ここで比の考え方を使っていますね。この計算式は、詳しく書けば、
(割合):(値段)= 10割(全額、100%、10割…全部同じことです):350円
なので、全額10割に対する3割は\(\displaystyle \times \frac{3}{10}\)すればいいです。
(割合):(値段)= 10割\(\displaystyle \times \frac{3}{10}\):350円\(\displaystyle \times \frac{3}{10}\) = 3割:105円
となります。先ほど言ったように、「比の計算は分数の掛け算で行う」という感覚を持っておいてください。
ですが、「3割引の商品はいくら?」という問いに対して、この105円を350円から引く、というのは若干手間です。
そこで、0.3を掛ける代わりに0.7を掛ける、という計算をします。
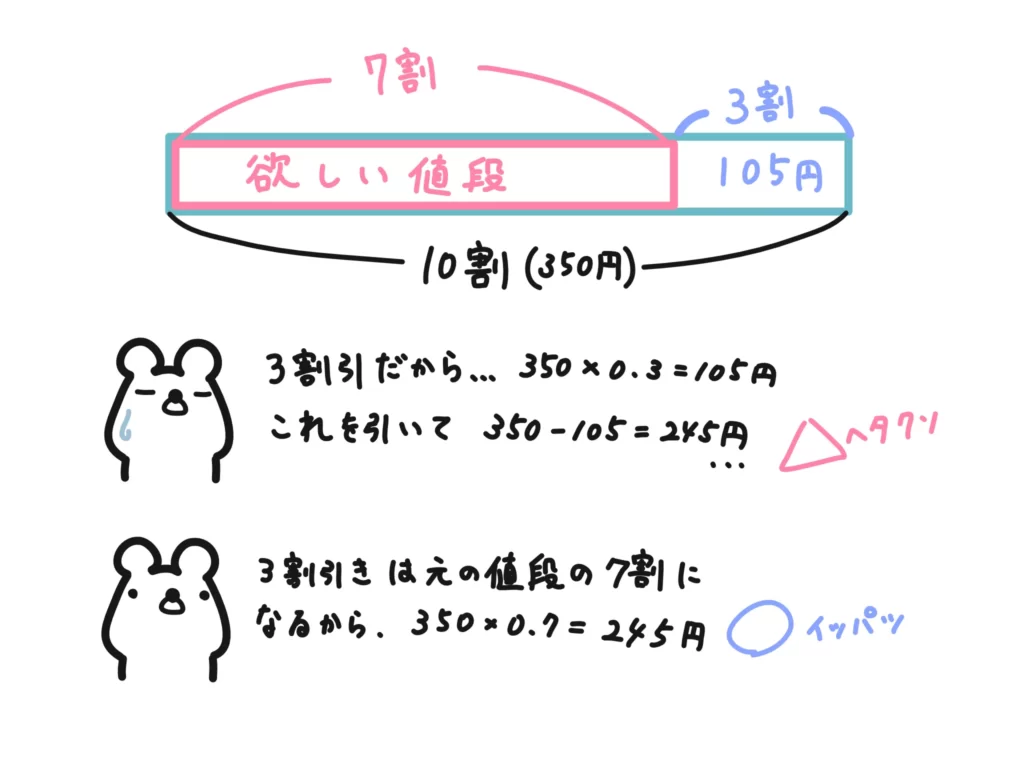

3割引のことを「7掛け」と言ったりしますね。これは、割り引いたあとの値段は、10割から3割を引いた7割に相当するからです。
同じく「2割引」だったら「残り8割の値段が欲しいので0.8を掛ける」し、「6割引」だったら「残り4割の値段が欲しいので0.4を掛ける」という計算をすれば、簡単に計算することができます。
計算上は「7を掛けて」下1桁の値を取っ払う(実際は0.7だから)という感じですが、実際には「350×7=2450だけど、元の値段は350円だから245円くらいだろ」という感覚で計算しちゃってもOKです。



全体を10としたときに、引いたのはいくらか?残ったのはいくらか?を割合で意識しておくと、こんな計算も楽チンです!
比の計算の応用「辺の長さ」
えー…これはできるようにしておいてください。高校でもよく使います。
例えば次のような問題です。
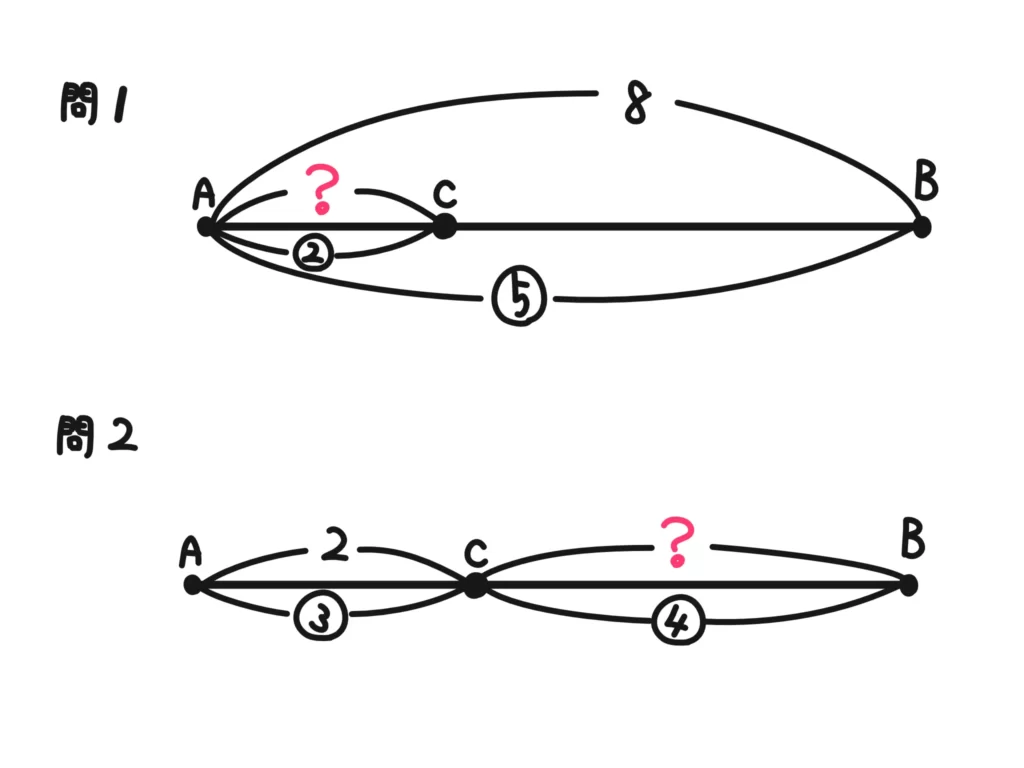

丸付きの数が比で、丸無しの数は長さ、とします。?の長さを求める、という問題です。



「簡単だよ!」という人はいいんですが、「ちょっと自信ない…」という人は、ここでしっかりと計算できるようにしておいてください。コツさえ掴めばそんなに難しくないですよ!
「比の計算は分数の掛け算で行う」のと、「1に対していくらになるか?それをあらかじめ計算しておこう!」という感覚を合わせれば、結構簡単にコツが掴めると思います。
例えば、問1に対して、
5:2 = 8 : \(x\)として、後で説明する「内項の積=外項の積」を使って計算することもできますが…面倒ですよね?
というか、「それでも計算できるからいいじゃん」という人は、こちらの記事も読んでもらえればな、と思います。勉強に対する大事な心構えも書いています。(高校生以上向けのお話です)


とにかく、「それで計算できるからいい」ではなく、「もっといいやり方があるなら積極的にそちらを学ぶべき」ということです。


今回の問1は、
\(\displaystyle 8 \times \frac{2}{5} = \frac{16}{5}\)
でイッパツです。この感覚を押さえておいてください。どのように考えるかというと、
- 基準となる値(今回は8)が、「比ではいくら」(今回は5)になるか確認する。
- 比1に対していくらになるか?を計算するために、『「比ではいくら(5)」という値で割る=分数の掛け算で言うと、分母にもってくる』。
- 欲しい値(今回は?)が「比ではいくら」(今回は2)になるか確認する。②の段階で比1に対していくらになるか?を計算しているので、あとは単純に『「比ではいくら(2)」という値を掛ける=分数の掛け算で言うと、分子にもってくる』。
つまり、(欲しい値)=(基準となる値)\(\displaystyle \times \frac{(欲しい値の比)}{(基準となる値の比)}\)で計算することができます。
問2は基準となる値が与えられている場所が違いますが、考え方は同じです。
(欲しい値)=(基準となる値)\(\displaystyle \times \frac{(欲しい値の比)}{(基準となる値の比)}\)で計算すると、
\(\displaystyle 2 \times \frac{4}{3} = \frac{8}{3}\)
でイッパツです。



これはイッパツで出せるようにしておいてください。
比の計算の応用「内項の積=外項の積」
比の計算でよく使う性質の1つに「内項の積=外項の積」というものがあります。
「内項の積=外項の積」
\(a:b = c : d \)のとき、
\(ad = bc\)
が成り立つ。
「比=比」で与えられたとき、=を挟んで内側にある項同士の積と外側にある項同士の積は等しい、という性質です。



言葉で説明するとまどろっこしいですね。式の形を見た方がわかりやすいと思います。
先ほどの「やるなよ!」といったやり方では、
5:2 = 8 : \(x\)
より、
\( 2 \times 8 = 5 \times x \) …※
\(\displaystyle x = \frac{16}{5}\)
という計算ができます。※部分が「内項の積=外項の積」ですね。
実は、内項の積と外項の積の関係も「説明して」と言われたら「?」となる性質の一つです。



簡単に説明しておきましょう。
先ほどの計算で説明します。
左辺の比だけ考えて操作してみましょう。
\((左辺の比)=5:2 = (5 \times 8) : (2 \times 8) = 40 : 16\)
ただ、8を掛けただけです。(もちろんこの8は右辺の比である「8」からきています。)
一方、右辺の比を考えて操作してみましょう。
\((右辺の比)=8:x = (8 \times 5) : (x \times 5) = 40 : 5x \)
ただ、5を掛けただけです。(もちろんこの5は左辺の比である「5」からきています。)
すると、それぞれ前項が「40」で揃ったので(もちろん揃うように操作しました)、これらの比が等しいということは、後項である「16」と「\(5x\)」は等しい、ということになります。
よって、\(16 = 5x\)となります。
一般的に\(a : b = c : d\)でも同じ考え方で説明できます。
\((左辺の比)=a:b = (a \times c) : (b \times c) = ac : bc\)
\((右辺の比)=c:d = (c \times a) : (d \times a) = ca : da = ac : ad\)
つまり、\(bc = ad\)となります。



ここまでの話で、比の式操作に慣れていれば簡単に説明できます。
ちなみに「内項の積=外項の積、どっかで説明しなかったかなぁ…」と思っていましたが、こちらで説明してました(書いた後に気づきました…)。
まぁ、若干方法は違うので、こちらも参考にしてください。
まとめ
比についての説明でした。
比は基本的な考え方でありながら、小学校で初めて目にする抽象的な考え方です。
ここらへんから「算数(数学)ってなんかよくわからん…」という数学苦手人生がはじまります…。
ですが、日常生活でもよく使いますし、知っていれば便利な考え方ですので、ぜひマスターして欲しいと思います!
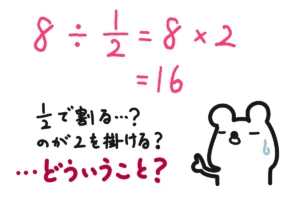
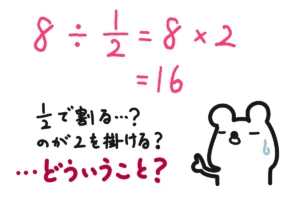


おまけ



ここからは本文に関係ない宣伝です。
このブログはアフィリエイト(宣伝)に参加しているのですが、アフィリエイトの広告って、結構面白いものがあるんですよね。
中には「なにコレ!欲しい!」と思うようなものもあります。結構アフィリエイトの広告って眺めているだけでも面白いです。
私は結構多趣味でパソコン関係からスポーツ、アウトドア、料理…色々やります。そんな私が、有名なASPサイトである「A8.net」と「もしもアフィリエイト」の広告を全て見て「これは面白いな」と思ったものや、実際に利用しているサービスを紹介していきたいと思います!



ちょっと息抜きに見てみてください!
LINEスタンプ



新着スタンプなど、情報発信していきます。他にも「クマ」に関する情報が共有できたら、と思います!



インスタは結構更新頻度高いです!ちょっとしたマンガも描いてますのでぜひフォローお願いします。
ポイ活
ポイ活は地味にお得なのでコツコツとやってます。買い物したりミニゲームしたりでポイントを稼ぐのが好きな人にはオススメです!



ネットショッピングをよくする、という人にオススメ!いろんなネットショッピングがポイントがつつ対象になってます。結構貯まりますよ。



