数学的帰納法って？コツをわかりやすく説明！

2022年9月20日

高校数学I A II Bの最大の山場、「数学的帰納法」…。

でも、受験勉強をすればするほど、ちょくちょく顔を出すコイツ…。

正直イヤだ！と思う人が大半ですが、味方につけたら心強いこともまた事実…。

こちらでも数学的帰納法をどんどん使っています。

数学的帰納法の説明に入る前に

たろぅ

…。

せんせ

どうかしました？

たろぅ

いや、すいません。数学的帰納法がホントにわかんないんですけど…。

せんせ

まぁ確かにわかりにくいところではありますね。
数学的帰納法のなにがわかんないんですか？

たろぅ

いや、なんかこう、全体的に何をしてるのかわかんないです。

せんせ

じゃあ最初から丁寧にいきましょうか。

たろぅ

よろしくお願いします。

まず、「数学的帰納法」というのは証明方法の一種です。

「この式や命題を証明したいなぁ」というときに使うのですが、実は教科書や参考書で（下手をしたら授業でも）あまり押さえられない、この証明方法を使う際の前提条件があります。それは、

「自然数」がからんでいる。
普通に証明しようとしても計算ができない、もしくは煩雑になる。

特に②です。これ、あまり明示的に言ってる教科書や参考書（や先生）、ないんじゃないでしょうか。

数学的帰納法の証明の基本は「等式・不等式の証明」です。等式・不等式の証明の基本はこちらの記事をご覧ください。

数学的帰納法の仕組み

ここが１つ目のよくわからないところだと思います。

まぁ実際は、ここは結構工夫した書き方をしている教科書、参考書も多いので「仕組みはなんとなくわかる」という人も多いと思います。

せんせ

とりあえず基本を押さえましょう。

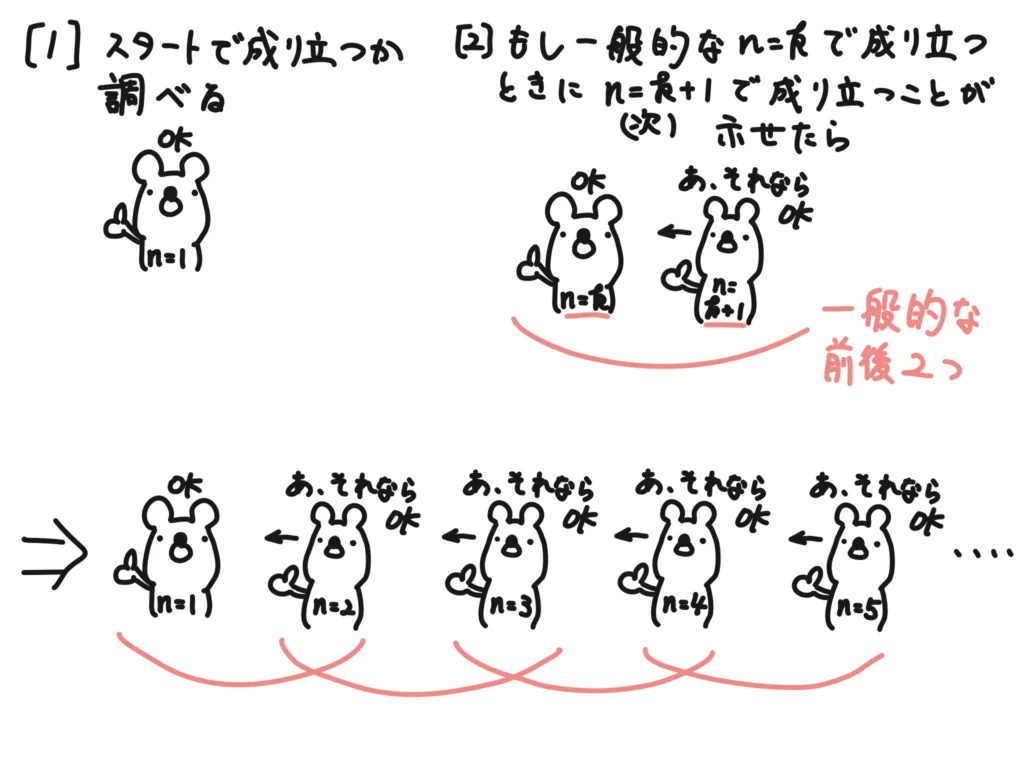
スタートの自然数で成り立つことを示す。大体は\(n=1\)だが、問題によって変わる。また、\(n=1\)のときと\(n=2\)のとき、のように複数の\(n\)についての証明が必要な場合もある。
\(n=k\)のとき成り立つと仮定したとき、\(n=k+1\)のときも成り立つことを示す。ここも、\(n=k\)と\(n=k+1\)で成り立つと仮定したとき、\(n=k+2\)のときも成り立つことを示す、であったり、問題によって変わる。

教員時代は、よくクラス内で手を上げさせてましたね。「前の人が手を上げたら自分も手を上げるんだよ」と全員に言っておいて、しばらく放置して「何も起きないよね？」と確認した上で、「じゃあ一番前の人手を上げて」って言ったら一列全員手を上げる、みたいな感じでやってました。

まぁ先ほど言ったように、このあたりはそれぞれ工夫していると思うので、仕組みはいいのかな、と思います。それでもわかりにくいので、まずは数学的帰納法の基本的な仕組みを理解してください。

実際に数学的帰納法の証明をしてみよう

これがメインです。

仕組みまでしっかり理解しているのに、実際に証明してみるとわからなくなる生徒が多いです。

結論から言うと、教科書や参考書の模範解答の書き方が、省略されていてわかりにくい、という部分に原因があるケースが多いです。

ポイントを押さえながら丁寧にやっていきます。

せんせ

まずは簡単な例題をみてみましょう。

全ての自然数\(n\)について、次の式が成り立つことを示せ。

\( \displaystyle 1 + 2 + \cdots + n = \frac{1}{2}n(n+1)\)

有名な自然数の和の公式ですね。等差数列として証明をした方がはるかに簡単なのですが、ここはあえて数学的帰納法で証明しましょう。

余談ですが、昔九州大学の大学入試問題でこれが出ましたね。最終的に\(1^3+2^3+\cdots+n^3\)まで証明するんですが、そのとき、いいか悪いか、ほとんどの生徒が数学的帰納法で証明していました。

せんせ

閑話休題、です。早速証明をしていきましょう。

\( \displaystyle 1 + 2 + \cdots + n = \frac{1}{2}n(n+1)\)…①

（証明）

[１]\(n=1\)のとき（左辺）\(=1\)、（右辺）\(\displaystyle=\frac{1}{2}\cdot 1 \cdot 2=1\)なので①は成り立つ

[２]\(n=k\)のとき①が成り立つとすると

\( \displaystyle 1 + 2 + \cdots + k = \frac{1}{2}k(k+1)\)…②

\(n=k+1\)のときを考えると、②から

\(\displaystyle 1+ 2+ \cdots +k+(k+1)=\frac{1}{2}k(k+1)+(k+1)\)

\(=\displaystyle \frac{1}{2}(k+1)(k+2)\)

よって、\(n=k+1\)のときにも①は成り立つ。

[１][２]から、すべての自然数\(n\)について①は成り立つ。（終）

たろぅ

…？（途中から、なんかわけわかんなくなったぞ）

こういう書き方をしている教科書や参考書が多いですね。もちろん１００％正しい証明なのですが、「初めて数学的帰納法を勉強する」という人に対してはちょっと不親切な書き方かな、と思います。

最初は面倒でももう少し丁寧に書くべきかな、と思いますし、いまだに私は丁寧に書きます。

自分が何を証明すべきか、が明確になるからです。

このタイプの書き方はそこをかなり省略して書いているので、パッと見たときに、わけがわからなくなるのだと思います。

それでは、私がいつも書いている形で証明をしてみましょう。

先に言っておきますが、書くのは面倒です。こうしなさい、というつもりもありません。ただ、数学的帰納法ってなにしてるのかわかんない、という人には「こういう仕組みで証明しているんだ」というのがわかっていいと思います。

また、先ほど言ったように、数学的帰納法の基本は「等式・不等式の証明」です。証明方法が特殊なのでこの基本が無視されがちですが、それを押さえるだけで何をしているかがグッとわかりやすくなります。

\( \displaystyle 1 + 2 + \cdots + n = \frac{1}{2}n(n+1)\)…①

（証明）

[１]\(n=1\)のとき（左辺）\(=1\)、（右辺）\(\displaystyle=\frac{1}{2}\cdot 1 \cdot 2=1\)なので①は成り立つ（←このへんも「等式の証明」の基本「左辺・右辺は別物」に従っています。）

[２]\(n=k\)のとき①が成り立つとすると

\( \displaystyle 1 + 2 + \cdots + k = \frac{1}{2}k(k+1)\)…②（←これは「成り立つとして使ってよい式」という認識）

\(n=k+1\)のとき（①の\(n \rightarrow k+1\)とした、）

\( \displaystyle 1 + 2 + \cdots + k + (k+1) = \frac{1}{2}(k+1)(k+2)\)…③を示す。（←ここを必ず書くようにしている。つまり、\(n=k+1\)のときのこの式は成り立っているかわかんないから、さっきの仮定を使って、コレを証明しますよ、という意味。繰り返しになりますが、等式の証明の基本に従います。）

（ここからは、③という等式を証明するんだ、というスタンスで記述していきます。）

（③の左辺）\( \displaystyle = 1 + 2 + \cdots + k + (k+1) \)

\(\displaystyle = \frac{1}{2} k(k+1) + (k+1) \)（②より）（←\(1+\cdots+k\)の計算が複雑なので、仮定を上手く使っている）

\(\displaystyle = \frac{1}{2}(k+1)(k+2)=\)（③の右辺）

よって、③が成り立つ（つまり、\(n=k+1\)のときにも①は成り立つ）。

[１][２]から、すべての自然数\(n\)について①は成り立つ。（終）

たろぅ

なるほど…仮定を使って\(n=k+1\)のときの等式の証明をする感じですね。

次は不等式の証明をしてみましょう。

３以上の自然数\(n\)について、次の不等式が成り立つことを示せ。

\( 2n < 2^n \)

これも不等式の証明の基本に従います。また「３以上の自然数\(n\)について」なので最初の[１]で証明すべきなのは\(n=3\)のときです。

\( 2n < 2^n \)…①

（証明）

[１]\(n=3\)のとき

①の（左辺）\(=2 \cdot 3 = 6\)、（右辺） \(=2^3=8\)より成り立つ。

[２]\(n=k\)のとき

①より\( 2k < 2^k \)…②（これは使ってよい式）

\(n=k+1\)のとき

\( 2(k+1) < 2^{k+1}\)…③となることを示す。（コレを今から証明する）

（③の右辺）ー（③の左辺）

\(= 2^{k+1}-2(k+1)\)

\(=2 \cdot 2^k-2(k+1)\)

\(>2 \cdot 2k -2(k+1)\)（②より）（←\(2^k\)を\(2k\)に置き換えたイメージ。すると、\( 2k < 2^k \)なので値としては小さくなる＆整式に揃うので計算ができるようになる）

\(=2k-2>0\)（←問題の条件に引っ張られて「\(k\)は３以上の自然数」になるから）

よって、（③の右辺）ー（③の左辺）\(>0\)になるので

③は成り立つ。

[１][２]より、３以上の自然数\(n\)について①は成り立つ。（終）

たろぅ

なるほど、なんとなくわかってきました。

おまけ「n=k、k+1の二つ必要なパターン」

問題によっては「\(n=k\)で成り立つ」という過程だけでは不十分なものもあります。

例えば次のような問題です。

\(n\)を自然数とする。\(a\)、\(b\)の２数について、この２数の和と積が整数であるとき、\(a^n+b^n\)は整数であることを示せ。

等式の証明…とは言えませんね。どちらかというと「整数の証明」です。ですが、実は数学的帰納法を使うべき条件を満たしています。

自然数がからんでいる。
\(a^n+b^n\)の計算は一般的な自然数\(n\)を使っているので、これ自体の計算は困難。

ということで、これも数学的帰納法を使いやすいです。

ただし、この証明については\(n=k\)のときに成り立つ、という仮定だけでは不十分です。その部分だけ抜き出して、先に話をしておきましょう。

まずは普通に\(n=k\)のときに成り立つと仮定する、という話で進めたいと思います。

…

[2]\(n=k\)のときに成り立つとする。つまり

\(a^k+b^k\)は整数である…②とする。

\(n=k+1\)のとき

\(a^{k+1}+b^{k+1}\)は整数である、ことを示す。

\(a^{k+1}+b^{k+1}=\) （←これを\(a^k+b^k\)を使って表したい）

\(a^{k+1}+ b^{k+1}\)を\(a^k+b^k\)で表すことができれば仮定②を使って証明できそうです。

ちなみに、このような文字を入れ替えても（\(a \leftrightarrow b\)と入れ替えても）式の意味が変わらない（\(a^n+b^n\)と文字を入れ替えた式\(b^n+a^n\)は式の意味としては変わりません）式を「対称式」といいます。

この対称式は「次数の低い対称式を上手く組み合わせることで表現できる」という性質があります。

つまり、\(a^{k+1}+ b^{k+1}\)は、それより次数の低い\(a^k+b^k\)をうまく使えば表現できる、ということですね。\((k+1)\)次式を\(k\)次式で表現していくので、\(a^k+b^k\)に１次式を掛ければ\(a^{k+1}+ b^{k+1}\)が表せるのではないか、というのがこの変形のとっかかりです。

せんせ

ということで、\(a\)と\(b\)を使った１次式で、一番シンプルな対称式（基本対称式）である\((a+ b)\)を掛けてみましょう。

\( ( a^k+b^k)(a+b)=a^{k+1}+b^{k+1}+a^kb+ab^k\)

確かに欲しい\(a^{k+1}+ b^{k+1}\)は出てきましたが、ジャマな\(a^kb+ab^k\)も出てきました。

対称式の変形は「ジャマな項を上手く打ち消していく」というのが基本方針です。

ということで、\(a^kb+ab^k\)を引いておきましょう。もしくは移項する、と考えてもOKです。

\( ( a^k+b^k)(a+b)-(a^kb+ab^k)=a^{k+1}+b^{k+1}\)

これで、\(a^{k+1}+ b^{k+1}\)を\(a^k+b^k\)で表すことができましたが、左辺には先ほどの\(a^kb+ab^k\)が残っています。これは\(a^k+b^k\)で表している、とは言えません。

\(a^kb+ab^k\)は、\(a\)と\(b\)の立場が入れ替わったような状態の項が足されています。そこで、この式から\(ab\)をくくりだします。

すると、\(a^kb+ab^k=ab(a^{k-1}+b^{k-1})\)となるので、先ほどの式は次のようになります。

\( ( a^k+b^k)(a+b)-ab(a^{k-1}+b^{k-1})=a^{k+1}+b^{k+1}\)…（※）

ここまで変形したらわかったと思いますが、\(a^{k+1}+ b^{k+1}\)は\(a^k+b^k\)だけでなく、そのひとつ前の\(a^{k-1}+b^{k-1}\)も必要だ、ということですね。つまり、連続する２つの自然数で成り立つと仮定して、その次の式が成り立つかどうか？を示した方がよさそうです。

ということは、\(n=k\)と\(n=k+1\)で成り立つ、と仮定して\(n=k+2\)のときに成り立つことを示していくのが、今回の数学的帰納法のポイントになります。

せんせ

前置きが長くなりましたが、この問題は\(a^n+b^n\)の変形がポイントです。そこさえわかれば、あとは数学的帰納法の「仕組み」の部分に着目して解くことができます。

ということで、

「\(n=k\)と\(n=k+1\)で成り立つ、と仮定して\(n=k+2\)のときに成り立つことを示していく」

という方針だというのがわかったので、最初の[１]も\(n=1\)だけではなく\(n=2\)のときも示します。

\(n=1\)だけ示しても、その後、「いや、２つ成り立たないと次が成り立たないんでしょ？」と言われるからです。

\(a^n+b^n\)は整数である…①

（証明）

[１]\(n=1\)のとき\(a^1+b^1=a+b\)なので、条件（\(a\)、\(b\)の和と積は整数）から①は成り立つ。

\(n=2\)のとき\(a^2+b^2=(a+b)^2-2ab\)なので、条件から①は成り立つ。（←スタートの２つを証明する）

[２] \(n=k\)と\(n=k+1\)のときに成り立つと仮定する。