相加相乗平均の大小関係証明集【完全版！】(2,3,4,n個)

2022年9月20日

こちらの記事で相加平均、相乗平均、調和平均について、その特徴と使い分けの説明をしました。

あわせて読みたい

平均の種類・求め方、いくつ知ってる？平均、と聞いたら、皆さん何を思い浮かべますか？ちなみに、どうでもいいですが令和３年の統計によると、サラリーマン（男性）の平均年収は約546万円らしいですよ。こ…

その際に、相加・相乗・調和平均の大小関係について、

（相加平均）\( \geq \) （相乗平均）\( \geq \) （調和平均）

が成り立つ、と紹介しました。

が、証明までしてなかったので、この記事では相加・相乗・調和平均の大小関係について証明していきます。

せんせ

今回は純粋に数学の証明を楽しんでもらえれば、と思います。

あと、超長いです。一気に全部読むとしんどいと思いますので、ぼちぼち必要な分だけ読んでください！

※ なるべく数学が苦手な人でも読みやすくするために、証明部分でも数学にそぐわない表現をしています。ご了承いただければ、と思います。あと、高校生の皆さんは、テストのときにはちゃんとした言葉遣いで証明を書いてくださいね。言葉遣いは自分の思考レベルを反映するので大事！

相加・相乗・調和平均の大小関係とは

せんせ

相加・相乗・調和平均の大小関係をもう一度、式で示しておきます。

\( a_1 , a_2 \cdots, a_n \)について、（ただし、\( a_1 \geq 0 , a_2 \geq 0 \cdots, a_n \geq 0 \)とする）

\( \displaystyle \frac{1}{n}(a_1 + a_2 + \cdots + a_n) \geq \sqrt[n]{a_1 \cdot a_2 \cdot \cdots \cdot a_n} \geq \displaystyle \frac{n}{\frac{1}{a_1} + \frac{1}{a_2} +\cdots + \frac{1}{a_n}} \)

の大小関係が成り立ちます。

ただし、等号成立は\( a_1 = a_2 = \cdots = a_n \)のときです。

せんせ

特に、高校の数学IIの段階では「相加・相乗平均の大小関係」という名前で、２つの数\(a\)、\(b\)について以下の式が成り立つ、という話でよく使います。

２つの数\(a\)、\(b\)について、（ただし\(a \geq 0\)、\(b \geq 0\)とする。）

\(\displaystyle \frac{a+b}{2} \geq \sqrt{ab} \)

が成り立ちます。

ただし、等号成立は\(a=b\)のときです。

高校数学では「他の問題を解くために応用しやすい」という理由で、相加平均の分母の２を払った次の形で使うことが多いです。

\(a+b\geq 2 \sqrt{ab} \)

が、まぁ本質的な意味はあんまりないです。「他の数学の問題が解きやすい」というだけです。

２つの数での証明

先ほどの、「２つの数について」の調和平均まで加えた式の証明をしていきます。

２つの数\(a\)、\(b\)について、（ただし\(a \geq 0\)、\(b \geq 0\)とする。）

\(\displaystyle \frac{a+b}{2} \geq \sqrt{ab} \geq \frac{2}{\frac{1}{a} + \frac{1}{b}}\)

が成り立ちます。

ただし、等号成立は\(a=b\)のときです。

せんせ

まずは、（相加平均）\( \geq\)（相乗平均）の証明をします。実はそこができたら、（相乗平均）\( \geq\)（調和平均）の証明はカンタンです。

教科書的な証明

（証明）

（相加平均）ー（相乗平均）

\(\displaystyle = \frac{a+b}{2} – \sqrt{ab} \)

\(\displaystyle = \frac{(\sqrt{a})^2+(\sqrt{b})^2-2 \sqrt{a} \sqrt{b}}{2} \) （←ここがポイント）

\(\displaystyle = \frac{(\sqrt{a}-\sqrt{b})^2}{2} \geq 0 \)（\( ( \quad )^2\)は0以上だから。これが0のときに等号成立）

よって、（相加平均）ー（相乗平均）\( \geq 0 \)なので、（相加平均）\( \geq\)（相乗平均）

また、等号成立は\(\displaystyle \frac{(\sqrt{a}-\sqrt{b})^2}{2} = 0 \)のときなので、\( \sqrt{a}-\sqrt{b}=0\)、つまり\(a=b\)のとき（終）

「ここがポイント」と書いたところがミソですね。\(a = (\sqrt{a})^2\)と捉えることで、\(x^2-2xy+y^2=(x-y)^2\)の因数分解を利用しています。

せんせ

\(a = (\sqrt{a})^2\)と捉えなければいけないので、条件である\(a \geq 0 \)が必要になってくるんですね（\(b\)も同様）。ルートの中身は0以上でなければいけませんからね。

（相乗平均）\( \geq\)（調和平均）の証明はカンタンです。

せんせ

先ほどの（相加平均）\( \geq\)（相乗平均）の\(a\)を\(\displaystyle \frac{1}{a}\)に、\(b\)を\(\displaystyle \frac{1}{b}\)に置き換えて式変形をしていけばOKです。

（証明）

（相加平均）\( \geq\)（相乗平均）の\(a\)を\(\frac{1}{a}\)に、\(b\)を\(\frac{1}{b}\)に置き換えると、

\(\displaystyle \frac{\frac{1}{a}+\frac{1}{b}}{2} \geq \sqrt{\frac{1}{a} \cdot \frac{1}{b}}\)が成り立ちます。

両辺の逆数をとって、

\(\displaystyle \frac{2}{\frac{1}{a}+\frac{1}{b}} \leq \sqrt{ab}\)（←両辺正なので、逆数をとると不等号の向きが入れ替わります）

よって、\(\displaystyle \sqrt{ab} \geq \frac{2}{\frac{1}{a}+\frac{1}{b}}\)、つまり（相乗平均）\( \geq\)（調和平均）が成り立ちます（終）

数学の問題の解き方になりますが、「前問利用」は重要なテクニックですね。

せんせ

最初にある式を証明、計算させておいて、次の問題に上手く利用してやる、というのはよくやりますね。

「前問利用」は苦手な生徒も多いのですが、ポイントもありますし、思考方法として重要な部分もありますので、そのうち記事にしたいと思います。

以降同様に、（相加平均）\( \geq\)（相乗平均）が示せたら、置き換えで（相乗平均）\( \geq\)（調和平均）も証明できるので、とりあえず（相加平均）\( \geq\)（相乗平均）を示していきます。

ちょっと面白い証明

せんせ

図形を使った面白い証明方法もあります。

せんせ

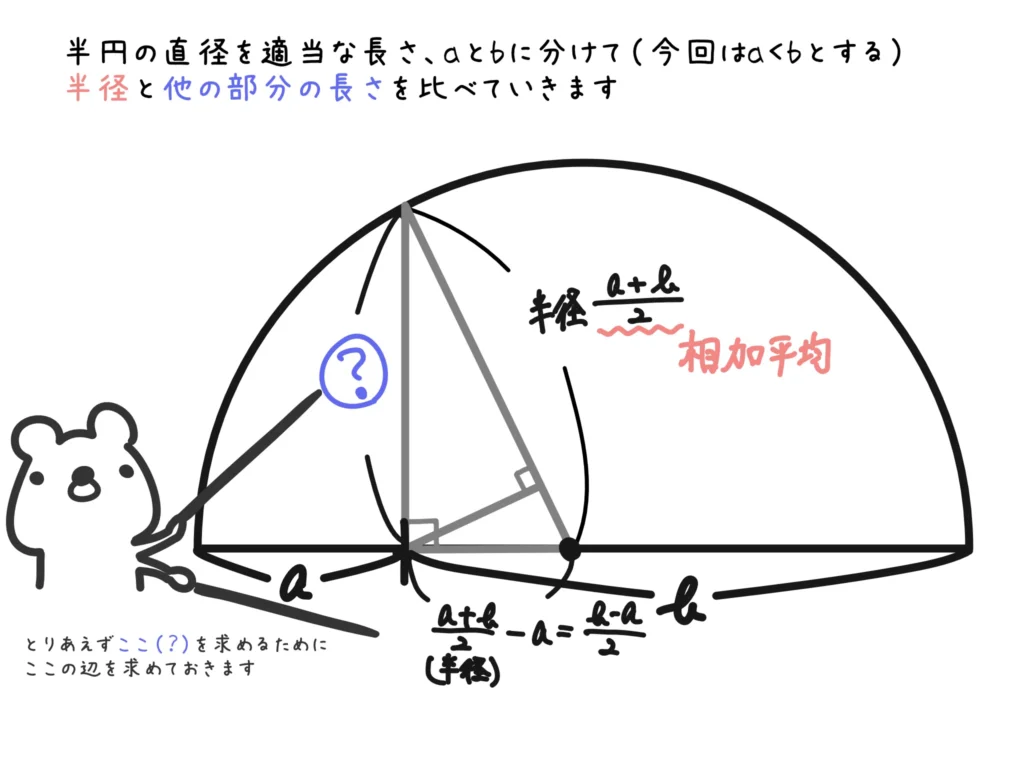
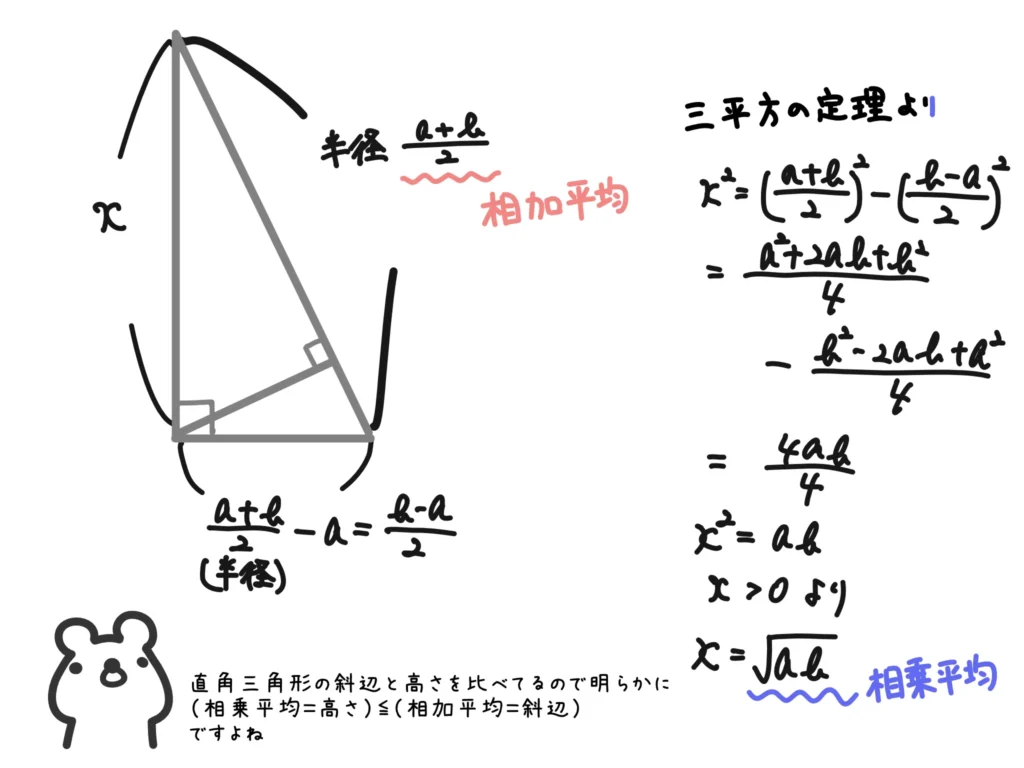
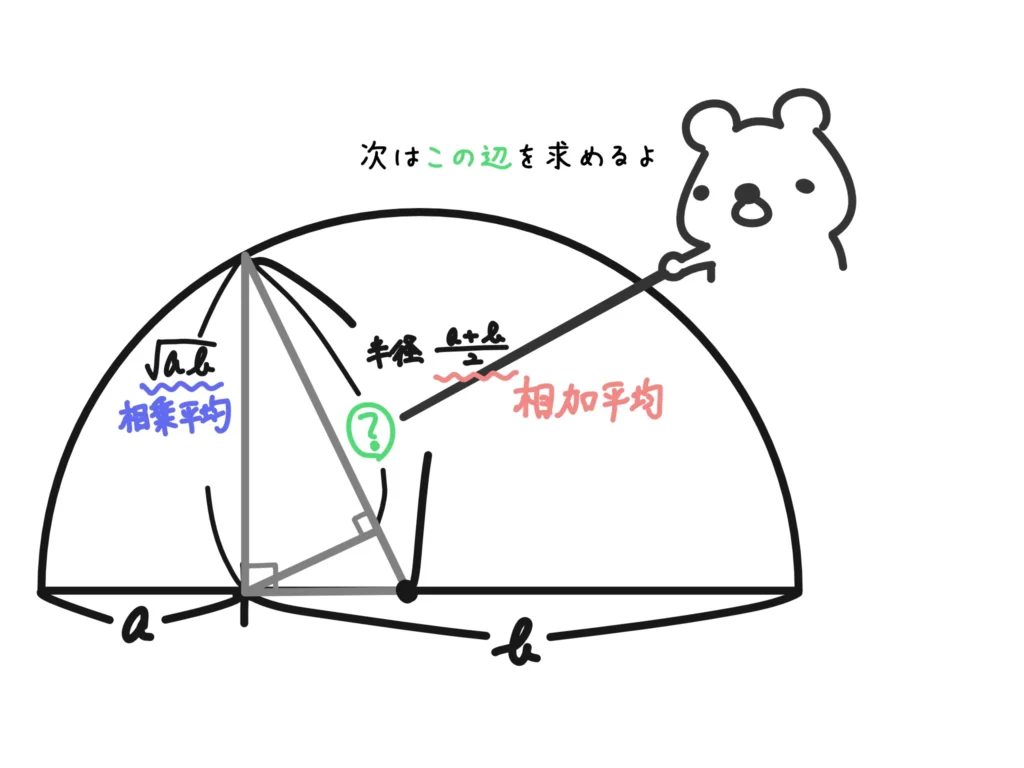
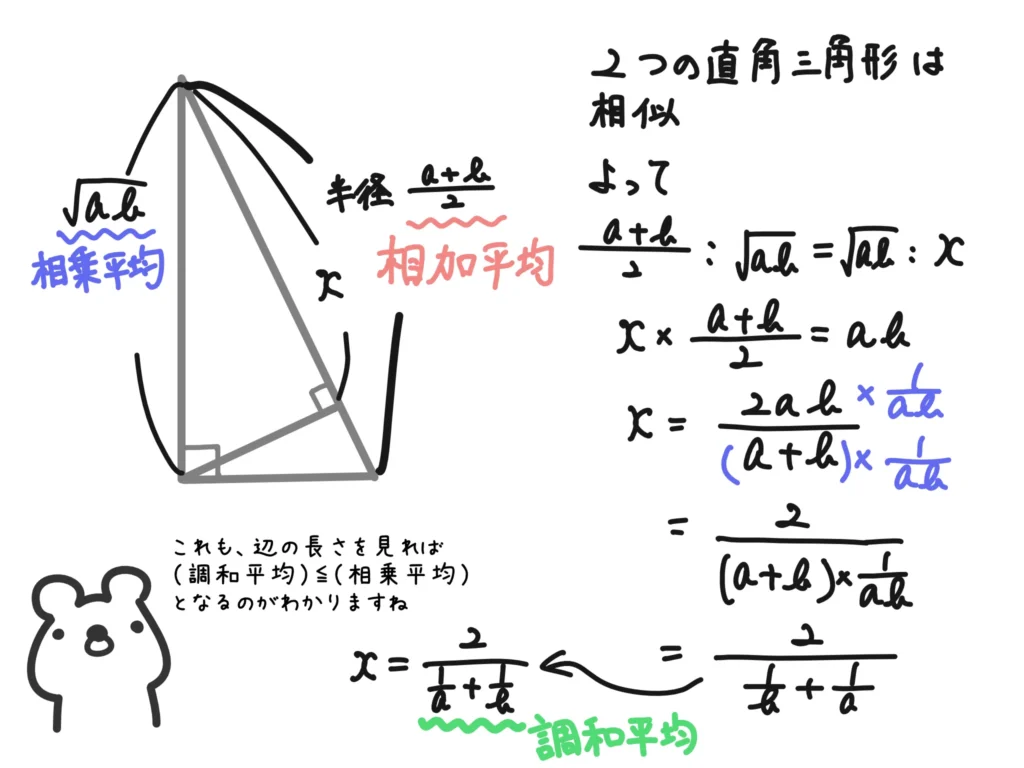
半円の中にできる直角三角形の辺の長さが相加・相乗・調和平均になる、というのは面白いですね！
大小関係も見たらわかりますし、等号成立も\(a=b=\)（半径）のときだ、というのがわかります。

図は\(a < b\)のときですが、\(a > b\)のときも同じように証明することができます。

４個の相加・相乗平均の大小関係

３個ではなく、先に「４個の場合」つまり

４つの数\(a\)、\(b\)、\(c\)、\(d\)について、（ただし\(a \geq 0\)、\(b \geq 0\)、\(c \geq 0\)、\(d \geq 0\)とする。）

\(\displaystyle \frac{a+b+c+d}{4} \geq \sqrt[4]{abcd}\)

が成り立ちます。

ただし、等号成立は\(a=b=c=d\)のときです。

せんせ

これを示していきます。これも先ほどと同様に２個の場合の（相加平均）\( \geq\)（相乗平均）を利用して証明できます。

（証明）

（相加平均）\( \geq\)（相乗平均）より

\(\displaystyle \frac{a+b}{2} \geq \sqrt{ab}\)、\(\displaystyle \frac{c+d}{2} \geq \sqrt{cd}\)が、とりあえず成り立ちます。

つぎに、\(\displaystyle \frac{a+b}{2} \)と\(\displaystyle \frac{c+d}{2} \)をそれぞれ１つの数とみなして、（相加平均）\( \geq\)（相乗平均）を使います。（どちらも0以上なので使ってOKです）

つまり、

\( \displaystyle \frac{\frac{a+b}{2}+\frac{c+d}{2}}{2} \geq \sqrt{\frac{a+b}{2} \cdot \frac{c+d}{2}} \cdots \)①

が成り立ちます。ここで、先ほど確認しましたが、\(\displaystyle \frac{a+b}{2} \geq \sqrt{ab}\)、\(\displaystyle \frac{c+d}{2} \geq \sqrt{cd}\)なので、①の右辺は、そのまま置き換えることができて、

\( \sqrt{\frac{a+b}{2} \cdot \frac{c+d}{2}} \geq \sqrt{\sqrt{ab}\sqrt{cd}} \)となります。つまり、①を考えると

\( \displaystyle \frac{\frac{a+b}{2}+\frac{c+d}{2}}{2} \geq \sqrt{\frac{a+b}{2} \cdot \frac{c+d}{2}} \geq \sqrt{\sqrt{ab}\sqrt{cd}}\)が成り立ちます。

真ん中の\( \sqrt{\frac{a+b}{2} \cdot \frac{c+d}{2}} \)を無視して考えると、

\( \displaystyle \frac{\frac{a+b}{2}+\frac{c+d}{2}}{2} \geq \sqrt{\sqrt{ab}\sqrt{cd}}\)、つまり

\(\displaystyle \frac{a+b+c+d}{4} \geq \sqrt[4]{abcd}\) となります。

等号成立は\(a=b\)かつ\(c=d\)かつ\(\displaystyle \frac{a+b}{2} =\frac{c+d}{2} \)、つまり\(a=b=c=d\)のとき（終）

「\(\sqrt[4]{\quad}\)とは？」という人は、こちらの記事をご覧ください。

あわせて読みたい

べき乗？マイナス乗？分数乗？ってなに？わかりやすく解説 \( 2^4 \)、計算できますか？じゃあ、\( 2^{-2} \)、計算できますか？「ん？」と思う人もいると思います。この記事では、指数部分にマイナスや分数がある、いわゆる…

3個の相加・相乗平均の大小関係

これはちょっとテクニカルです。なので、「へぇ、面白いな」と思ってもらえればいいかな、と思います。

3つの数\(a\)、\(b\)、\(c\)について、（ただし\(a \geq 0\)、\(b \geq 0\)、\(c \geq 0\)とする。）

\(\displaystyle \frac{a+b+c}{3} \geq \sqrt[3]{abc}\)

が成り立ちます。

ただし、等号成立は\(a=b=c\)のときです。

これを証明していきます。

まずは、以下の因数分解の公式が成り立つことを知っておいてください。

\( a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca) \)

あまり有名でない公式ですが、高校生で大学受験を考えている人はこの公式を覚えておいた方がいいです。

また、\(-3abc\)を移項して変形した、

\( a^3+b^3+c^3 = (a+b+c)(a^2+b^2+c^2-ab-bc-ca)+3abc \)

の形も、\(a^3+b^3+c^3\)の式変形として使うことがあるので、押さえておきましょう。

せんせ

3個の相加・相乗平均の大小関係の証明については、この式を使います。

（証明）

\( a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca) \)

\(\displaystyle =(a+b+c)\{ \frac{1}{2}(2a^2+2b^2+2c^2-2ab-2bc-2ca) \} \)（←2つ目の()をあえて\(\frac{1}{2}\)でくくる）

\(\displaystyle =\frac{1}{2}(a+b+c)(a^2-2ab+b^2+b^2-2bc+c^2-2ca+a^2) \)（←\(2a^2=a^2+a^2\)のようにここもあえて、\(a^2\)、\(b^2\)、\(c^2\)を分けて並び替える）

\(\displaystyle =\frac{1}{2}(a+b+c) \{ (a-b)^2+(b-c)^2+(c-a)^2)\} \geq 0 \)（\(a \geq 0\)、\(b \geq 0\)、\(c \geq 0\)だから）…①

よって、\( a^3+b^3+c^3-3abc \geq 0\)なので、\( a^3+b^3+c^3 \geq 3abc\)

→\( \displaystyle \frac{a^3+b^3+c^3}{3} \geq abc\)

ここで、この式の\(a \Rightarrow \sqrt[3]{a}\)、\(b \Rightarrow \sqrt[3]{b}\)、\(c \Rightarrow \sqrt[3]{c}\)と置き換えると、

\( \displaystyle \frac{(\sqrt[3]{a})^3+(\sqrt[3]{b})^3+(\sqrt[3]{c})^3}{3} \geq \sqrt[3]{a} \sqrt[3]{b} \sqrt[3]{c} \)

\(\displaystyle \frac{a+b+c}{3} \geq \sqrt[3]{abc}\)

等号成立は①の\((a-b)^2+(b-c)^2+(c-a)^2\)部分が0のときなので、\(a=b=c\)（終）

せんせ

あえて\(\displaystyle \frac{1}{2} \)でくくって、\(2a^2=a^2+a^2\)と分ける、というところがポイントですね。
面白いこと考えますよね。

n個の相加・相乗平均の大小関係の証明は結構ムズカシイ…

２個、３個、４個はどうにか証明できますが、n個の相加・相乗平均の大小関係になると、最低でも数学B「数列」で習う数学的帰納法か、数学IIIの知識が必要になります。

長くなるので「見てみたい！」という人は↓をめくって見てください！

「数学的帰納法を使った証明」

（証明）

①\(n=k\)のときに成り立つと仮定すると、\(n=2k\)のときに成り立つことを示す。

\(n=k\)のときに成り立つと仮定すると、

\( \displaystyle \frac{1}{k}(a_1 + a_2 + \cdots + a_k) \geq \sqrt[k]{a_1 \cdot a_2 \cdot \cdots \cdot a_k} \)

（これは「k個の数で相加相乗平均の大小関係が成り立つ」という意味。別にk個の数であれば、\( a_1 , a_2 \cdots, a_k \)じゃなくてもいい）

\(n=2k\)のとき、\( \displaystyle \frac{1}{2k}(a_1 + a_2 + \cdots + a_{2k}) \geq \sqrt[2k]{a_1 \cdot a_2 \cdot \cdots \cdot a_{2k}} \)が成り立つことを示す。

（左辺）\(= \displaystyle \frac{1}{2} \frac{a_1 + a_2 + \cdots a_k +a_{k+1} +\cdots+ a_{2k}}{k}\)

\(= \displaystyle \frac{1}{2} ( \frac{a_1 + a_2 + \cdots a_k}{k} +\frac{a_{k+1} +\cdots+ a_{2k}}{k} ) \)

\( \geq \displaystyle \frac{1}{2} ( \sqrt[k]{a_1 \cdot a_2 \cdot \cdots \cdot a_k} +\sqrt[k]{a_{k+1} \cdot \cdots \cdot a_{2k}} ) \)（「k個の数で相加相乗平均の大小関係が成り立つ」という仮定から）

\(= \displaystyle \frac{ \sqrt[k]{a_1 \cdot a_2 \cdot \cdots \cdot a_k} +\sqrt[k]{a_{k+1} \cdot \cdots \cdot a_{2k}} }{2}\)

\(\geq \displaystyle \sqrt{ \sqrt[k]{a_1 \cdot a_2 \cdot \cdots \cdot a_k} \cdot \sqrt[k]{a_{k+1} \cdot \cdots \cdot a_{2k}} }\)（\(\sqrt[k]{a_1 \cdots a_k}\)、\(\sqrt[k]{a_{k+1} \cdots a_{2k}}\)でもう一回相加相乗平均の大小関係を使った）

\(= \displaystyle \sqrt[2k]{a_1 \cdot a_2 \cdot \cdots a_{2k}}\)

よって、\( \displaystyle \frac{1}{2k}(a_1 + a_2 + \cdots + a_2k) \geq \sqrt[2k]{a_1 \cdot a_2 \cdot \cdots \cdot a_{2k}} \)が成り立つ。つまり、\(n=k\)のとき成り立つとすると、\(n=2k\)のときにも成り立つ。

②\(n=k+1\)のとき成り立つと仮定すると、\(n=k\)のときに成り立つことを示す。

\(n=k+1\)のとき成り立つ、ということは、「k+1個の数で相加相乗平均の大小関係が成り立つ」という意味。

\( a_1 , a_2 \cdots, a_k \)と、k+1個目の数\(\displaystyle \frac{a_1 + a_2 + \cdots + a_k}{k} \)で相加相乗平均の大小関係を作ると、

\(\displaystyle \frac{a_1 + a_2 + \cdots + a_k+\frac{a_1 + a_2 + \cdots + a_k}{k}}{k+1} \geq \sqrt[{k+1}]{a_1 \cdot \cdots a_k \cdot \frac{a_1 + a_2 + \cdots + a_k}{k} }\)

\(\displaystyle \frac{\frac{k a_1 + k a_2 + \cdots + k a_k+a_1 + a_2 + \cdots + a_k}{k}}{k+1} \geq \sqrt[{k+1}]{a_1 \cdot \cdots a_k \cdot \frac{a_1 + a_2 + \cdots + a_k}{k} }\)

\(\displaystyle \frac{\frac{(k+1) a_1 + (k+1) a_2 + \cdots + (k+1) a_k}{k}}{k+1} \geq \sqrt[{k+1}]{a_1 \cdot \cdots a_k \cdot \frac{a_1 + a_2 + \cdots + a_k}{k} }\)

\(\displaystyle \frac{a_1 + a_2 + \cdots + a_k}{k} \geq \sqrt[{k+1}]{a_1 \cdot \cdots a_k \cdot \frac{a_1 + a_2 + \cdots + a_k}{k} }\)

両辺\(k+1\)乗して、

\(\displaystyle (\frac{a_1 + a_2 + \cdots + a_k}{k})^{k+1} \geq a_1 \cdot \cdots a_k \cdot \frac{a_1 + a_2 + \cdots + a_k}{k} \)

両辺\( \frac{a_1 + a_2 + \cdots + a_k}{k} (>0)\)で割って、

\(\displaystyle (\frac{a_1 + a_2 + \cdots + a_k}{k})^{k} \geq a_1 \cdot \cdots a_k \)

両辺\(k\)乗根をとって、

\(\displaystyle \frac{a_1 + a_2 + \cdots + a_k}{k} \geq \sqrt[k]{a_1 \cdot \cdots a_k} \)

よって、\(n=k+1\)のとき成り立つと仮定すると、\(n=k\)のときに成り立つ。

①、②より、すべての自然数で相加相乗平均n個Verが成り立つ。（終）

数学的帰納法＋数学IIIの「微分」を使う

（証明）

\(n=k\)のときに成り立つと仮定すると、\(n=k+1\)のときに成り立つことを示す。

つまり、\(\displaystyle \frac{a_1 + a_2 + \cdots + a_{k+1}}{k+1} \geq \sqrt[k+1]{a_1 \cdot \cdots a_{k+1}} \)が成り立つことを示す。

（左辺）ー（右辺）

\(= \displaystyle \frac{a_1 + a_2 + \cdots + a_{k+1}}{k+1} – \sqrt[k+1]{a_1 \cdot \cdots a_{k+1}} \)

\(= \displaystyle \frac{a_1(1 + \frac{a_2}{a_1} + \cdots + \frac{a_{k+1}}{a_1})}{k+1} – \sqrt[k+1]{a_1^{k+1}\cdot 1 \cdot \frac{a_2}{a_1}\cdots \frac{a_{k+1}}{a_1}} \)

\(= \displaystyle \frac{a_1(1 + \frac{a_2}{a_1} + \cdots + \frac{a_{k+1}}{a_1})}{k+1} – a_1 \sqrt[k+1]{ \frac{a_2}{a_1}\cdots \frac{a_{k+1}}{a_1}} \)（←\(a_1^{k+1}\)をk+1乗根から出せる）

\(= \displaystyle a_1 (\frac{1 + \frac{a_2}{a_1} + \cdots + \frac{a_{k+1}}{a_1}}{k+1} – \sqrt[k+1]{ \frac{a_2}{a_1}\cdots \frac{a_{k+1}}{a_1}} ) \)

\(\geq \displaystyle a_1( \frac{1 + k \sqrt[k]{\frac{a_2}{a_1} \cdots \frac{a_{k+1}}{a_1}}}{k+1} – \sqrt[k+1]{ \frac{a_2}{a_1}\cdots \frac{a_{k+1}}{a_1}}) \)…①（←\(n=k\)のときに相加相乗平均の大小関係が使えるので\( \frac{a_2}{a_1} + \cdots + \frac{a_{k+1}}{a_1} \geq k \sqrt[k]{\frac{a_2}{a_1} \cdots \frac{a_{k+1}}{a_1}}\)）

ここで、()の中を調べるために、\(\displaystyle \frac{a_2}{a_1} \cdots \frac{a_{k+1}}{a_1}=x\)とした、\(\displaystyle f(x)=\frac{1+k \sqrt[k]{x}}{k+1}-\sqrt[k+1]{x}\)（\(x>0\)）について調べる。

\(f'(x)=\frac{1}{k+1}x^{\frac{1}{k}-1}-\frac{1}{k+1}x^{\frac{1}{k+1}-1}=\frac{1}{k+1} x^{\frac{1}{k+1}-1}(x^{\frac{1}{k}-\frac{1}{k+1}}-1) \)

\(f'(x)=0\)とすると、\(x=1\)。増減表は次のようになる。

\(x\)	0	…	1	…
\(f'(x)\)		–	0	+
\(f(x)\)		\( \searrow \)	0	\( \nearrow \)

よって、\(x>0\)で\(f(x)>0\)なので、①についても0以上、となるので、\(n=k+1\)のときも成り立つことが示せた。

等号成立は、途中で使った相加相乗平均の大小関係の等号成立条件、\(\displaystyle \frac{a_2}{a_1} = \cdots =\frac{a_{k+1}}{a_1}\)と、\(f(x)=0\)つまり\(\displaystyle \frac{a_2}{a_1} \cdots \frac{a_{k+1}}{a_1}=1\)が成り立つときなので、\( a_1 = a_2 = \cdots = a_k = a_{k+1} \)のとき（終）

\( e^x\)に関わる性質を上手いこと使う

これはエレガントです！

（証明）

\(e^x\)について、\(e^x \geq x+1\)…①

が成り立つ。これは\(f(x)=\)(左辺)-(右辺)として、微分すれば証明できる。教科書例題レベルだけど、有名な不等式。

さて、\(m=\displaystyle \frac{1}{n}(a_1+\cdots + a_n)\)として、\( \displaystyle x= \frac{a_k}{m}-1 \)を①に代入。

\(\displaystyle e^{ \frac{a_k}{m}-1} \geq \frac{a_k}{m} \)

これを\(k=1, 2, \cdots , n\)まで準備して、辺々掛ける。

\(\displaystyle e^{ (\frac{a_1}{m}-1)+(\frac{a_2}{m}-1)+\cdots+(\frac{a_n}{m}-1)} \geq \frac{a_1}{m} \cdot \frac{a_2}{m}\cdot \cdots \cdot \frac{a_n}{m} \)

\(\displaystyle e^{ \frac{a_1+a_2+\cdots+a_n}{m}-n } \geq \frac{a_1 \cdot a_2 \cdot \cdots \cdot a_n}{m^n} \)

ここで、\(m=\displaystyle \frac{1}{n}(a_1+\cdots + a_n)\)を変形すると、\( \frac{a_1+a_2+\cdots+a_n}{m}-n=0\)。

つまり、不等式の左辺の指数部分は0なので、

\(\displaystyle 1 \geq \frac{a_1 \cdot a_2 \cdot \cdots \cdot a_n}{m^n} \)

\(\displaystyle m^n \geq a_1 \cdot a_2 \cdot \cdots \cdot a_n \)

n乗根をとって、

\(\displaystyle m \geq \sqrt[n]{a_1 \cdot a_2 \cdot \cdots \cdot a_n} \)

よって、\( \displaystyle \frac{1}{n}(a_1 + a_2 + \cdots + a_n) \geq \sqrt[n]{a_1 \cdot a_2 \cdot \cdots \cdot a_n}\)

等号成立は、①が等号成立するときなので、\(x=0\)のとき（調べてね）。

ゆえに、それぞれの\(k\)のときに、\( \displaystyle x= \frac{a_k}{m}-1=0 \)となればよいので、\( a_1 = a_2 = \cdots = a_n \)。

せんせ

…さすがにお腹いっぱいです。ここまでよく読みました！