PR
べき乗?マイナス乗?分数乗?ってなに?わかりやすく解説

\( 2^4 \)、計算できますか?
じゃあ、\( 2^{-2} \)、計算できますか?
「ん?」と思う人もいると思います。
この記事では、指数部分にマイナスや分数がある、いわゆる「べき乗」について説明していきます。
「自然数乗」と「0乗」
まずは普通の「自然数乗」からいきましょう。
先ほどの\( 2^4 \)は、「2が4個掛かっている」状態を表します。
\( 2^4 = 2 \times 2 \times 2 \times 2 = 16 \) ですね。
次に「0乗」についてですが、先ほど「2が4個掛かっている」と言いましたが、「何に?」というのが重要ですね。答えは「1に」です。
ということで、\(2^0 \)と言ったら、「1に2が0個掛かっている」という意味になりますので、
\(2^0=1\)となります。
マイナス乗
さて、ここからですね。
数学というのは、考え方を拡張していきたがる、という特徴があります。
指数部分が0以上の整数だったら、というのは先ほど説明しましたが、じゃあ「指数部分がマイナス」だったらどうなるんだろう?という具合に考え方を拡張していきます。
考え方としては、以前紹介した(マイナス)×(マイナス)=(プラス)の話と似ています。
 せんせ
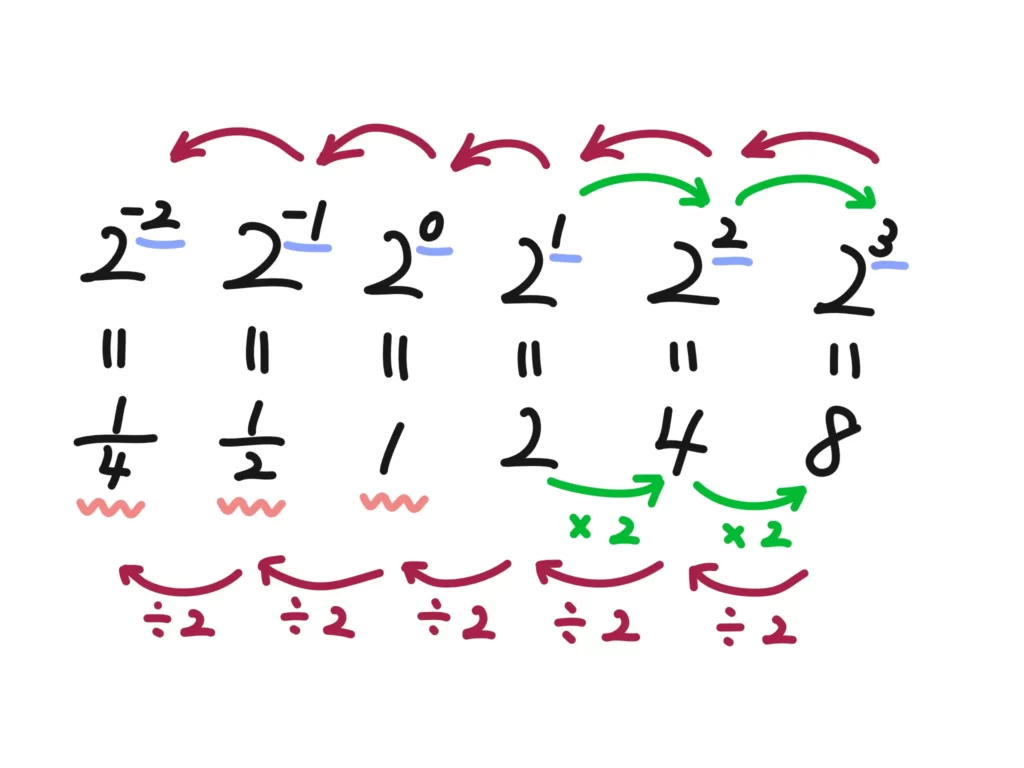
せんせ例えば、\(2^2=4\)、\(2^3=8\)、\(2^4=16\)という具合に指数部分を1増やすということは、計算としては2を掛けている、ということになります。



なるほど、これはなんとなく覚えてますよ。マイナス×マイナスのときのイメージを応用すればいいんですよね?つまり、指数部分を1減らしたら逆に2で割っている、と捉えるんですね。



その通り!その考え方で指数部分を拡張していって、マイナス乗を定義するんですね。先ほどの0乗も、こちらの考え方でも定義できます。

ということで、指数に関する以下の重要な性質が得られます。
・ \( \displaystyle a^{-1} = \frac{1}{a} \)。これを基本のイメージとして持っておくのをオススメします。
これを拡張すると、
\( \displaystyle a^{-n} = \frac{1}{a^n} \)となります。ただし、nは整数です。
・ また、\( \displaystyle a^m \div a^n = a^m \times \frac{1}{a^n} = a^m \times a^{-n} \)となるので、\( \div \)の記号は「\( -n \)乗の掛け算」に直すことができます。



こう定義すると、指数法則も無理なく拡張できるんですよね。



…(指数法則ってなんだっけ?)



…その顔は指数法則、覚えてないですね?
指数法則、というのは指数に関する以下の法則です。
【指数法則】
- \(a^n \times a^m = a^{n+m} \)
- \( ( a^n)^m = a^{nm} \)
- \( ( a \times b )^n = a^n \times b^n \)
例えば、
- \(2^3 \times 2^2 = 2^{3+2} = 2^5 \)
- \( (2^3)^2 = 2^{3 \cdot 2} = 2^6 \)
のような感じですね。これが、指数部分がマイナスでも上手いこと成り立ってくれます!
- 指数部分がマイナスのときに一つ目の指数法則を使ってみます。\( 2^3 \times 2^{-2} = 2^{3-2}=2^1 \) 。これは先ほどの\(\displaystyle 2^{-2} = \frac{1}{2^2} \)を使うと、\(\displaystyle 2^3 \times 2^{-2} = 2^3 \times \frac{1}{2^2} = 2^1 \)と説明できるので、確かに一つ目の指数法則が成り立ちます。
- 指数部分がマイナスのときに二つ目の指数法則を使ってみます。\( (2^3)^{-2} = 2^{3 \cdot (-2)} = 2^{-6} \)。これも同様に、\( \displaystyle (2^3)^{-2}=\frac{1}{(2^3)^2} = \frac{1}{2^{2 \cdot 3 }} = \frac{1}{2^6} = 2^{-6} \)となり、確かに二つ目の指数法則が成り立ちます。



やはり重要なのは、\(\displaystyle a^{-n} = \frac{1}{a^n} \)ですね。これを左→右、右→左に変形することで、確かに指数部分がマイナスのときも成り立つことが説明できます。
数学をモチーフにしたオシャレなオリジナルグッズも販売中です!おかげさまで好評頂いてます!
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ!
累乗根とは?
次は「分数乗」の話なのですが、この累乗根というものを知っておかないと、その話ができません。ですので、累乗根の説明を簡潔に、具体的にしていきたいと思います。



では問題です。「\(a\)の平方根とは何か?を説明しなさい」。



平方根ってルートのことでしょ?



ぶっぶー!!ぜんっぜんちがいますね。もう、ぜんぜんです。



あれぇ…平方根ってルートのことじゃなかったっけ?ん?平方根とルートってなにが違うんだろ…?(←だんだん酷い扱いを受けるのに慣れてきている。)
「\(a\)の平方根」とは、「2乗したら\(a\)になる数」のことです。
例えば、「4の平方根は?」=「2乗すると4になる数は?」=「\( \pm 2\)」となります。\( 2^2=4\)、\((-2)^2=4\)なので、確かにどちらも「2乗すると4になる数」ですね。
「2の平方根は?」=「2乗すると2になる数は?」=「\( \pm \sqrt{2} \)」となります。ここで、「2乗すると2になる数」を整数で表すことができないので、ルートという記号を導入したわけですね。
では本題です。
「2乗したら\(a\)になる数」の考え方を拡張して、「3乗したら\(a\)になる数」、「4乗したら\(a\)になる数」、…「n乗したら\(a\)になる数」のことをn乗根と呼ぶことにします。
例えば、「8の3乗根は?」という具合ですね。「8の3乗根は?」=「3乗すると8になる数は?」=「\(2\)」となります。今回は\( -2\)は8の3乗根ではないですね。\( (-2)^3=-8\)だからです。
「2の3乗根は?」と聞かれたら、これも新たな記号を導入してあげる必要があるのがわかると思います。そこで、ルートと同様に「3乗したら2になる数」を「\( \sqrt[3]{2}\)と書こう」と決めます。\( \sqrt[3]{\quad}\)のことを3乗根、と言います。
ということで、一般的に「n乗したら\(a\)になる数」を「n乗根」といい、「\( \sqrt[n]{a}\)(場合によっては\( \pm \sqrt[n]{a}\)となる)」と書きます。



「ここまで知ってるよ」とか「とりあえず累乗根ってのがあるんだ、ふーん」という人は次に進んでくれてOKです。「もう少し累乗根について知りたいんだけど」とか「累乗根の計算の練習したい!」という人は、以下のアコーディオンメニューをクリックしてみてください!
累乗根について、もう少し知りたい人はコチラ!
累乗根について、もう少し詳しい説明をしていきます。
累乗根についてもう少し
① ルートとは違って、\( \sqrt[3]{(-8)} \)とかいうのは、あり得ます。「3乗したら−8になる数」なので\( \sqrt[3]{(-8)} = -2\)となります。
② 例えば、3乗根のイメージからわかると思いますが、\( ( \sqrt[3]{2} )^3 =2 \)です。
③ 2乗根は\(\sqrt[2]{a}\)と書きますが、ルートのことなので\(\sqrt[2]{a}=\sqrt{a}\)のように、「2」を省略します。
累乗根の性質
とりあえず、累乗根には以下のような性質があります。
- \( \sqrt[n]{a} \times \sqrt[n]{b}=\sqrt[n]{ab} \)
- \( ( \sqrt[n]{a} )^m = \sqrt[n]{a^m} \)
- \( \sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a} \)
- \( \sqrt[n]{a^m} = \sqrt[pn]{a^{pm}} \)
なぜこうなるのか、は次の分数乗の説明を聞いた方がわかりやすいかもしれません。
例1.\( \sqrt[3]{2} \times \sqrt[3]{4} = \sqrt[3]{2 \times 4} = \sqrt[3]{8} = 2 \)
例2.\( \sqrt{\sqrt[3]{64}} = \sqrt[2 \cdot 3]{64} = \sqrt[6]{2^6} = (\sqrt[6]{2})^6 = 2 \)
例3.\( (\sqrt[4]{3})^2 = \sqrt[2 \cdot 2]{3^2} = \sqrt[2]{3}=\sqrt{3} \)



まぁ、累乗根の計算練習もいいですけど、累乗根と次の分数乗の関係を把握して、指数法則で計算した方がわかりやすいですけどね.
分数乗



さて、では分数乗ですね。例えば\( 2^{\frac{1}{2
}}\)ってなんだろう?と考えたときに、マイナス乗と同様に
どうすれば妥当な定義ができるのか、ということです。



さっきのマイナス乗は指数を減らしていけばマイナスになる、という取っ掛かりがありましたけど、今回は全くイメージができません…。



そうですね。
ヒントは「ちゃんと指数法則が成り立ってほしい」というところです。今のところ(指数部分がマイナスを含む整数でも)指数法則が成り立っているので、分数乗を導入しても成り立ってほしいです。計算が統一的にできますからね。



例えば、\( (2^{ \frac{1}{2}})^2\)の計算で指数法則が成り立つとしましょう。
指数法則が成り立つとすれば、
\( (2^{ \frac{1}{2}})^2 = 2^{ \frac{1}{2} \times 2} = 2^1 = 2\)
となります。



この式は\( 2^{ \frac{1}{2}} \)を2乗してますよね?



そうですね。



結果はどうなってます?



「2」ですね。まぁ、指数法則が成り立つとすれば、ですけど。



そうですね。じゃあ確認ですが、この「\( 2^{ \frac{1}{2}} \)は、○乗したら△になる数」ですか?



えー…「\( 2^{ \frac{1}{2}} \)は2乗したら2になる数」ですね。



それって、なんでしたっけ?



あ…。
「2乗したら2になる数」…これは平方根のことですね。正確には\( 2^{ \frac{1}{2}} \)にはマイナスがついていないので、平方根のプラスの方、つまり\( \sqrt{2} \)のことです。



\( 2^{ \frac{1}{2}} =\sqrt{2} \)…ということですか?



今のところ、そう捉えたら良さそう、ということですね。もう少し一般的に拡張してから、確認してみましょう。
一般的に指数法則が分数乗で成り立つとすると、\( ( a^{\frac{1}{n}} )^n =a^{\frac{n}{n}}=a^1=a \)となるので、\(a^{\frac{1}{n}} \)はn乗したら\(a\)になる数、つまり\(a\)のn乗根(の正の方)と言えそうです。



なるほど、\(a^{\frac{1}{n}} = \sqrt[n]{a} \)ということですね!



そうですね。もう少し具体的に指数法則が成り立つか、確認をしていきましょう。
【指数法則】(再掲)
- \(a^n \times a^m = a^{n+m} \)
- \( ( a^n)^m = a^{nm} \)
- \( ( a \times b )^n = a^n \times b^n \)
2つ目は「これが成り立つとすると」という話から始めたので、成り立ちます。3つ目も成り立つのはすぐにわかるでしょう。
1つ目について、これが成り立つかどうか確認してみます。
とりあえず計算してみると、\( 2^{ \frac{1}{2}} \times 2^{ \frac{1}{2}} =2^{ \frac{1}{2}+\frac{1}{2}}=2^1=2 \)ですが、\( 2^{ \frac{1}{2}} =\sqrt{2} \)とすると、
\( \sqrt{2} \times \sqrt{2} = 2 \)なので、確かに1つ目の指数法則が成り立ちそうです。
もう一つ具体的な計算をしてみましょう。先ほどの、\(a^{\frac{1}{n}} = \sqrt[n]{a} \)となる、と考えると、例えば\(2^{\frac{1}{3}} = \sqrt[3]{2} \)となりますね。これで1つ目の指数法則が成り立つか確認してみましょう。
\( 2^{ \frac{1}{3}} \times 2^{ \frac{1}{3}} =2^{ \frac{1}{3}+\frac{1}{3}}=2^{\frac{2}{3}}=(\sqrt[3]{2})^2 \)ですね。
一方、\( 2^{ \frac{1}{3}} \times 2^{ \frac{1}{3}} = \sqrt[3]{2} \times \sqrt[3]{2}= (\sqrt[3]{2})^2\)となるので、問題なく指数法則が成り立ちそうです。



確かに、いけそうですね…。
まとめ
今回は指数の拡張について説明しました。よく知っている指数について、指数部分がマイナス、分数のときに以下のような性質が成り立つのは面白いですね。
- \(\displaystyle a^{-n} = \frac{1}{a^n} \)
- \( a^{\frac{1}{n}} = \sqrt[n]{a} \)
指数の意味として「\(a^n\)は\(a\)がn個掛かっている」ということであれば、nは0以上の整数、と考えるのが普通だと思います。
しかし、「もしこうだったらどうだろう?」「それに正しく意味をもたせることができるだろうか?」と想像力を働かせて、論理的に正しい定義をしてあげることで、数学の世界はどんどん広がっていきます。
想定する力と、イメージを矛盾なく具体化するための論理力は現実世界でも重要ですね。