PR
共役な複素数とは?これを見れば共役な複素数の重要性質がわかる!

複素数とは、「二乗すると\(-1\)になる虚数単位\(i\)」という数を使って表される、次のような形をした数です。
\( a+bi\)(ただし、\(a\)、\(b\)は実数)
これに対し、\(+bi\)の部分の符号をひっくり返した、
\( a-bi\)
を「共役(きょうやく)な複素数」と言い、重要な役割があります。
 せんせ
せんせ読み方は「きょうえき」じゃないよー。
「きょうやく」だよー。
特に数学C「複素数平面」(旧数学III)レベルの話で複素数を扱うようになってくると、複素数平面上での意味や、計算上、その役割が増えてきます。
この記事では「共役な複素数」って何に使えるのか?を解説していきます。
共役な複素数とは?



共役な複素数ってなんですか?



(無視してもいいかな)



無視しないでくださーい!聞こえてないんですかぁ??質問に答えてくださーい!!



わかりましたよ…。「共役な複素数」でしょ?



確か、虚部の符号が違う複素数じゃなかったですかね…



そうですね!で?で?なんか役に立つの!!?



(そんなん、知らんわな)
共役な複素数…。共役な複素数とは、
\(a +bi\)に対して\(a – bi\)のこと
です。
この共役な複素数、計算上とても重要な役割を果たします。
共役な複素数「和と積が実数になる」
試してくれればすぐにわかりますが、元の複素数とその共役な複素数の和と積は実数になります。
複素数\(a+bi\)(\(a\)、\(b\)は実数)について、共役な複素数は\(a-bi\)になりますが、
その和は、
\( (a+bi)+(a-bi) = 2a\)となり実数となります。
また、積も、
\( (a+bi)(a-bi) = a^2-(bi)^2\)
\( = a^2+b^2\)
となり実数となります。
特に積の結果、\(a^2+b^2\)は複素数\(a+bi\)の絶対値の2乗になります。
「絶対値?」という人はこちら。




積が実数になるので、共役な複素数は分数において「分母の実数化」に使いますね。
例.
\( \displaystyle \frac{1}{1+2i} = \frac{1-2i}{(1+2i)(1-2i)}\)
\( \displaystyle \quad= \frac{1-2i}{1^2+2^2}=\frac{1-2i}{5}\)
共役な複素数「複素数平面でいうと、実軸の反対側」
複素数平面を考えてくれたらわかりますが、\(a+bi\)に対して、\(a-bi\)は実軸の反対側にきます。
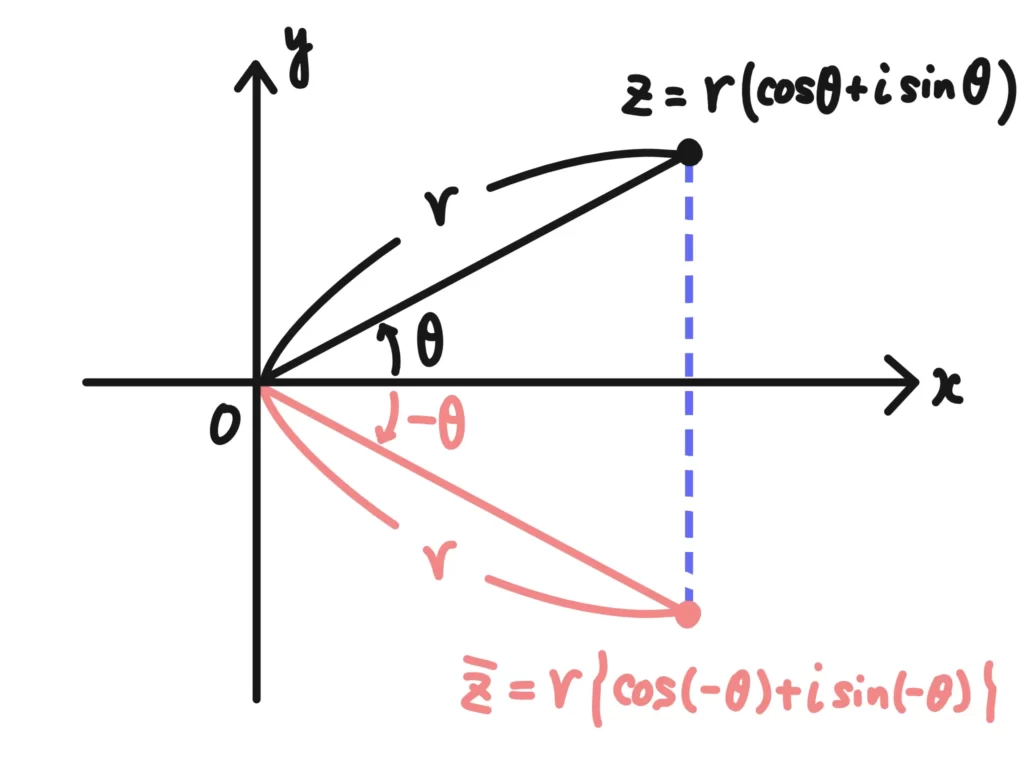

そして、図を見てくれたらわかりますが、\(a+bi=r(\cos{\theta}+i\sin{\theta})\)とした場合、共役な複素数\(a-bi\)は偏角が\(-\theta\)になります。



この偏角の性質と積の性質を使えば、先ほどの「積は絶対値の2乗になる」というのもすぐにわかります。
\(a+bi=r(\cos{\theta}+i\sin{\theta})\)に対して、共役な複素数は\(a-bi=r \{ cos{(-\theta)}+i\sin{(-\theta)} \} \)
よって、\( (a+bi)(a-bi)\)は
\( (a+bi)(a-bi) = r^2 \{ \cos{(\theta-\theta)}+ i \sin{(\theta-\theta)} \} \)
\( \quad = r^2 ( \cos{0} + i \sin{0})=r^2 \)



なるほど…複素数平面まで考えたら、また別のアプローチができますね。
複素数の掛け算と極形式についてはコチラの記事も合わせてご覧ください。

共役な複素数「実数条件」



なるほど…共役な複素数という「複素数のペア」を考えると面白い性質があるんですね。



ほー…複素数のペアねぇ…。



え…なんか間違ってます?



複素数のペアがいつでもできると思っているのか!?



(なんか急に怒られた?)
共役な複素数がペアで出てくる、ということは、複素数\(z\)に対して、共役な複素数\( \overline{z}\)が、
\( z \neq \overline{z}\)として出てくる、ということです。



そりゃそうですよ。「ペアで出てくる」って言ったら\(z=\overline{z}\)になったらおかしいでしょ?



ふーん…じゃあ\(z=\overline{z}\)とはならないんですね?



え…そんなことあります?
さて、では少し計算して確認しましょう。
\( z = a+bi \)とします。
もし、\(z = \overline{z}\)とすると、
\( a+bi = a-bi \)
\( 2bi = 0 \)
\( b = 0 \)



ん…もしかして\(b=0\)のとき、\(z = \overline{z}\)になるんですか?でも\(b=0\)って…。



そうですね。 \( b =0\)のとき\( z = \overline{z}\)、とも言えます。



\(b = 0\)のときって、虚数なんですか?
ここまで言ったらわかると思います。「\(a+bi\)の\(b=0\)のとき」と言ったら\(a+bi = a\)ですよね。



これってただの実数なんじゃないですか?
その通りです!\(b=0\)のとき、複素数\(a+bi\)は実数となります!
つまり、
\(z = \overline{z}\)のとき\(z\)は実数。
となります。



共役な複素数\(\overline{z}\)を使って\(z=\overline{z}\)を考えたら、それが成り立つとき「実数になる」ということですね。



なるほど…。複素数を考えているときに、それが実数かどうか?は重要な条件になりますよね。
おまけ「三次方程式が共役な複素数を解に持つことの証明」
先ほどの実数条件を使えば、実数係数の方程式が虚数解をもつとき、共役な複素数を解に持つことを簡単に示すことができます。
ただし、合わせて共役な複素数に関する次の性質も使います。
- \( \overline{\alpha + \beta} = \overline{\alpha}+ \overline{\beta}\)
- \( \overline{\alpha \cdot \beta} = \overline{\alpha} \cdot \overline{\beta}\)



それでは、共役な複素数を解に持つことを証明してみましょう!
今回は三次方程式で示しますが、他の次数でも示し方は同じです。
問.実数係数の方程式\( a x^3 + b x^2 + c x + d=0\)が虚数解\(z\)を解に持つとする。このとき、\(z\)の共役な複素数\(\overline{z}\)もこの方程式の解であることを示せ。
(証)
\(z\)は \( a x^3 + b x^2 + c x + d=0\)の解なので、
\( a z^3 + b z^2 + c z + d=0\)が成り立つ。つまり、
\( \overline{a z^3 + b z^2 + c z + d}=\bar{0}\)も成り立つ。
\( \overline{a z^3} + \overline{b z^2} + \overline{c z} + \overline{d}=0\)
\( \overline{a}\overline{z^3} + \overline{b}\overline{ z^2} + \overline{c}\overline{z} + \overline{d}=0\)
\( a(\overline{z})^3 + b(\overline{z})^2 + c(\overline{z}) + d = 0\)(←\(a\)、\(b\)、\(c\)、\(d\)は実数だから。\(\overline{a}=a\)などが成り立つ)
よって、\(\overline{z}\)も\( a x^3 + b x^2 + c x + d=0\)の\(x\)に代入すれば成り立つので、\(\overline{z}\)も方程式\( a x^3 + b x^2 + c x + d=0\)の解(終)
まとめ
共役な複素数の性質について確認しました。
特に共役な複素数と「実数」とは密接な関係がある、というのがわかったと思います。
複素数を考えているときに、それが実数かどうか?というのはかなり大きな条件になります。
普段は「常に実数」を扱っているので、あまり実感することがないと思いますが、複素数の話をしているときにはそれが大きい条件になってきます。
特に「実数条件\(z=\overline{z}\)」は押さえておきましょう。




複素数平面をしっかり学習したら、ぜひこちらも読んでみてください。
『数学ガールの秘密ノート』シリーズは基本から丁寧に話が進んでいくのでわかりやすいですし、なにより物語として面白いのでオススメです!



