PR
「分数で割る」ときなぜ逆数を掛ける?割り算の「分け方」は2通り
今回は、誰もが思う「ある数を分数で割るってどういうこと?」という疑問にお答えしていきます!
「分数で割るって…分母分子をひっくり返して掛ければいいんでしょ?」
と思っている方。それはそうなのですが「なぜそうするの?」と聞かれたら困りますよね。
この理由を丁寧に説明していきます。
意外とわからない、割り算の持つ意味についても解説していきます!
分数で割るってどういうこと?
 せんせ
せんせ太郎くん…。



ん?なんですか?



ここの分数計算間違ってますよ。



あ、ヤバい…。



計算ミスはただのうっかりミスじゃありませんよ。重大なミスだと思わないと直りませんよ。気をつけてください。



いやぁ、分数の割り算ってミスしやすいんですよ。



でも、ひっくり返して掛けるだけじゃないですか。



うーん…。それ、小学校のときから疑問なんですよね。なんで分数ひっくり返して掛けるんですか?



じゃあ説明してください。



え!?「なんで」って聞いてるのに、僕が説明しなきゃならないんですか?
ということで、皆さんは分数の割り算をするときに、分母と分子をひっくり返して掛ける、というのはご存知だと思います。
ただ、「なぜそうするの?」と聞かれたら、なかなか答えられないと思います。下手したら学校の先生でも答えられないと思います。
ちなみに分母と分子をひっくり返したものを逆数と言います。
正確には、\(a\)に対して、\(a \times b = 1\)となる\(b\)のことを、\(a\)の逆数と言います。
例えば、\(\displaystyle \frac{1}{4}\)の逆数は\(\displaystyle \frac{4}{1}=4\)です。\(\displaystyle \frac{1}{4} \times 4 = 1\)となるからです。
それではまず「割り算の持つ意味」から確認していきましょう!
割り算が持つ意味



じゃあヒントです。解答の式が\(8 \div 2\)となるように問題を作ってください。



\(8 \div 2\)が計算式になる問題を作ればいいんですね?えーっと…「8粒のイクラを2人で分けると一人何粒ですか?」



(イクラ8粒…)まぁ、正解ですね。もう一つ作れますか?



え…。えーっと、「8粒の明太子を2人で分けると一人何粒ですか?」



それだと、実は割り算の「分け方」は同じなんですよね。



へ?割り算の「分け方」?分け方に種類があるんですか?
実は割り算には2つの「分け方」があります。
今太郎くんが作ってくれた例題は「割られる数を割る数で分ける」イメージですね。個人的に、このイメージは割り算の(比較的)普通の感覚かな、と思います。
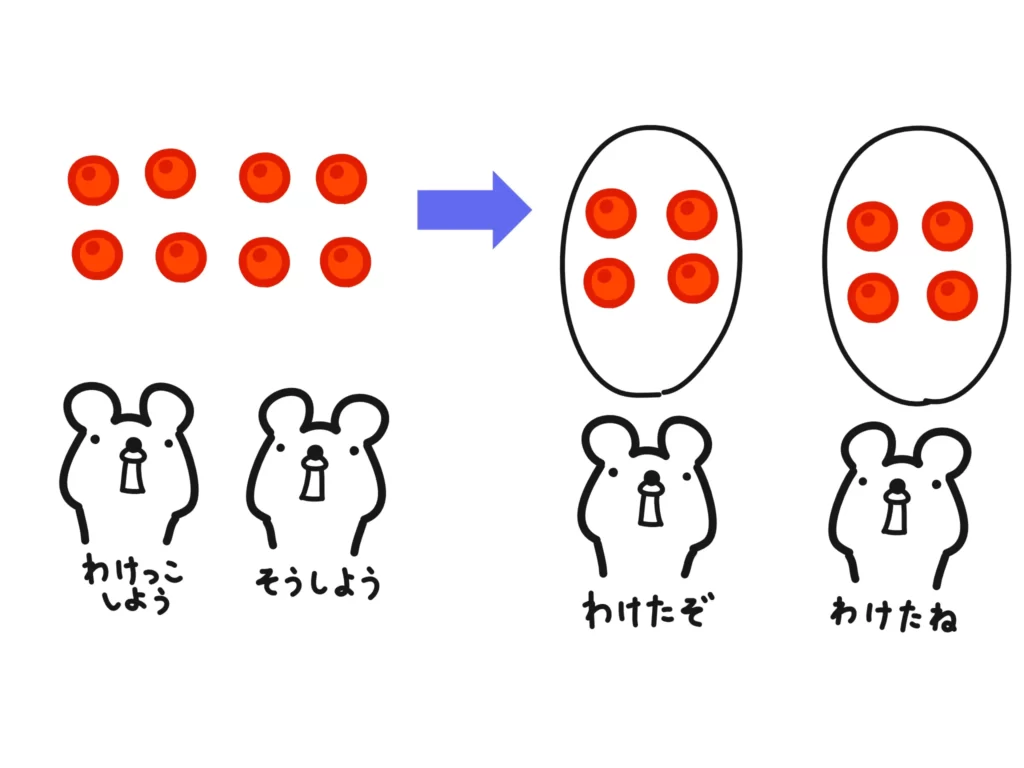

ですが、実はこちらの感覚では分数の割り算が説明しにくいんです。



例えば「数の子8粒を2粒ずつにして分けると、何人に配れますか?」という問題だと、どういう計算になりますか?



あぁ、確かにそれでも\(8 \div 2\)になりますね。でも…数の子8粒って笑



…(合わせたんだろうがよ)
割り算にはこのイメージもあるんですね。言われてみれば、という感じですよね。まぁ、「当たり前じゃん」と思う人もいると思います。
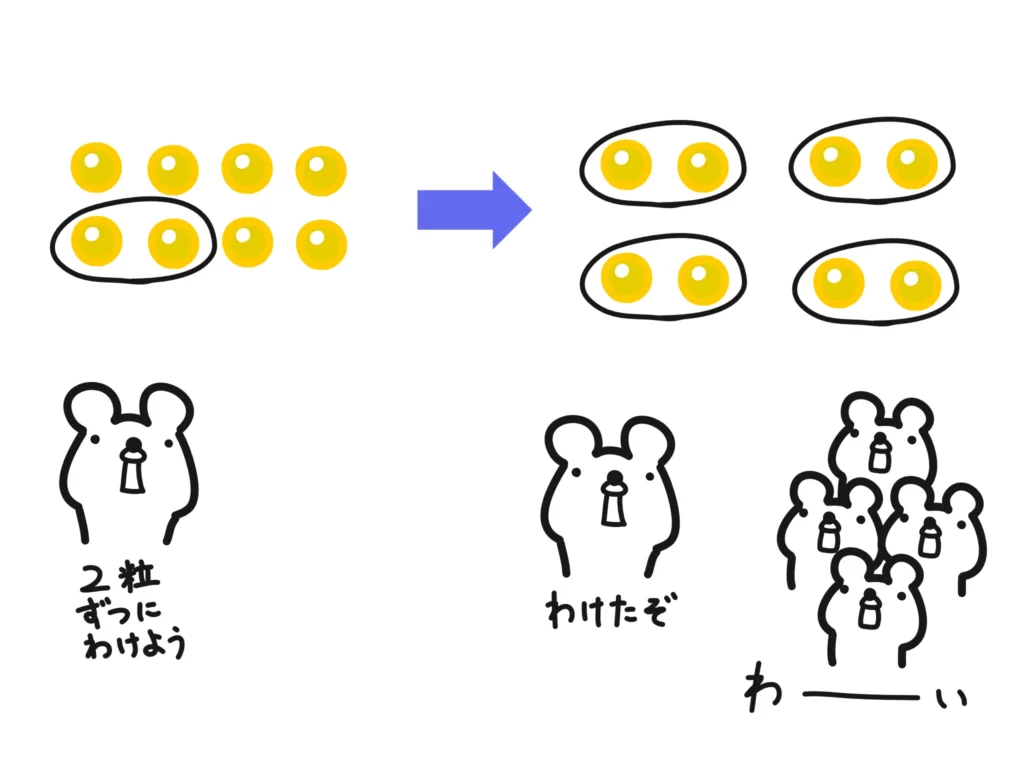

この「割る数を1セットとみなしたとき、割られる数はいくつに分けられますか?」という考え方を使うと、分数の割り算がわかりやすいです。
分数で割ることを「これを1セットとしたとき、割られる数は何セットに対応するか?」で理解する
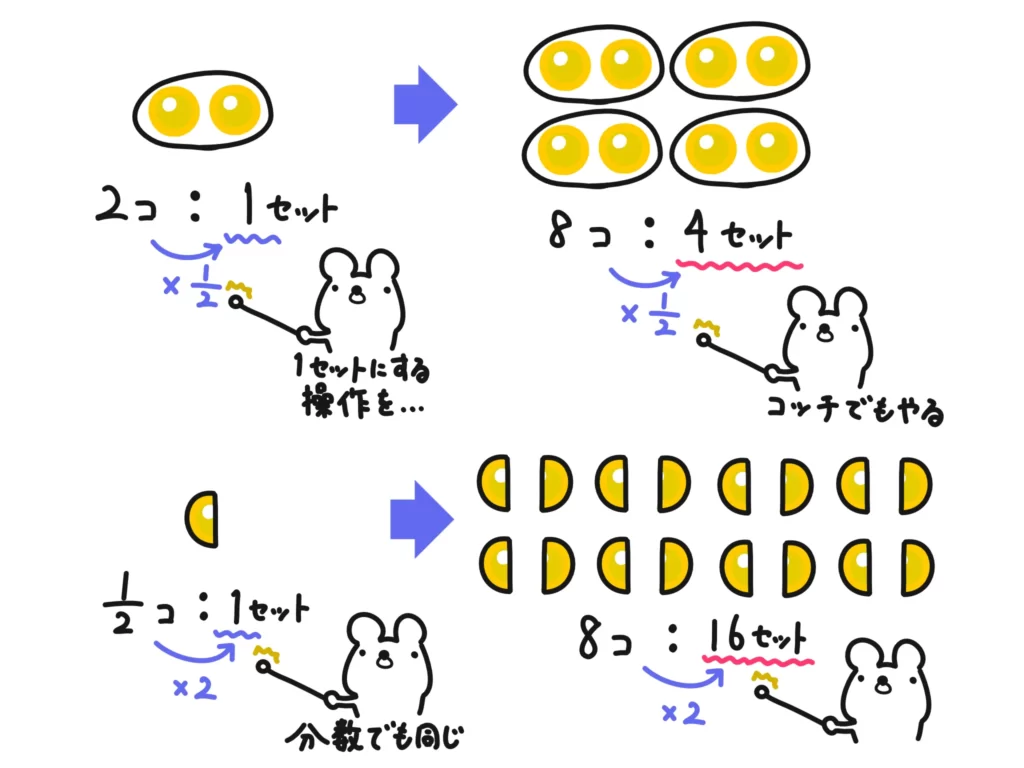
例えば\( 8 \div 2 = 4\)について、次の2つの考え方ができます。
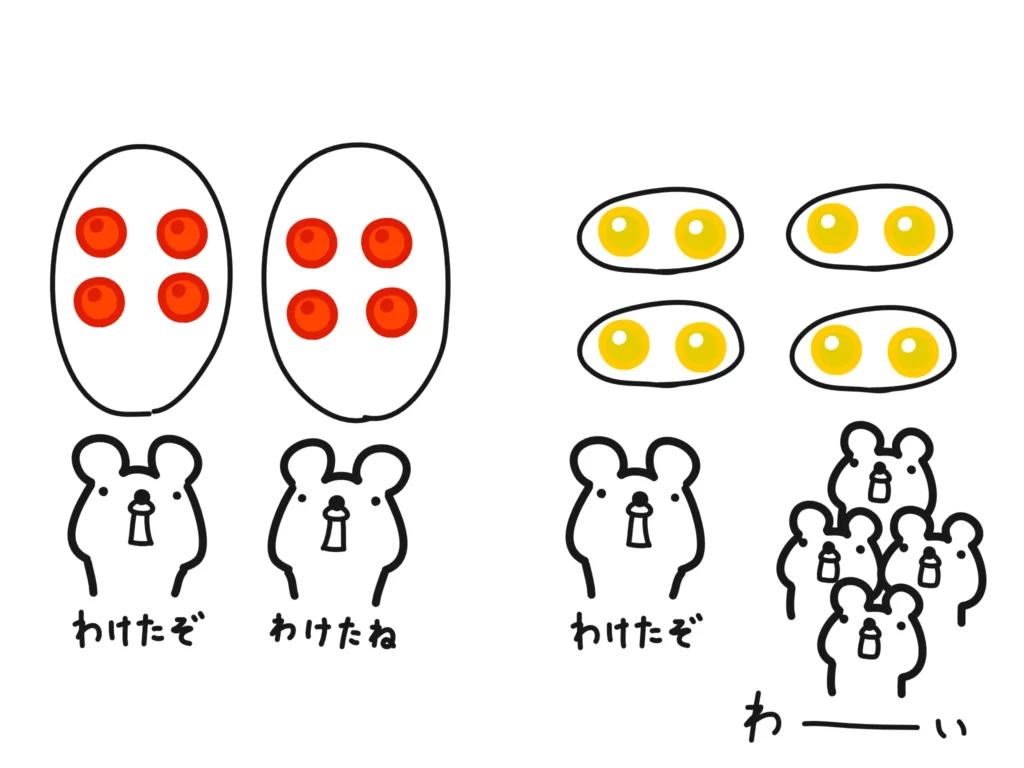

右の図は「8は、2を1セットとしたときに、4セットに分けられる」という考え方ですね。
これを\(\displaystyle 8 \div \frac{1}{2} \)でも同じように考えてみましょう。
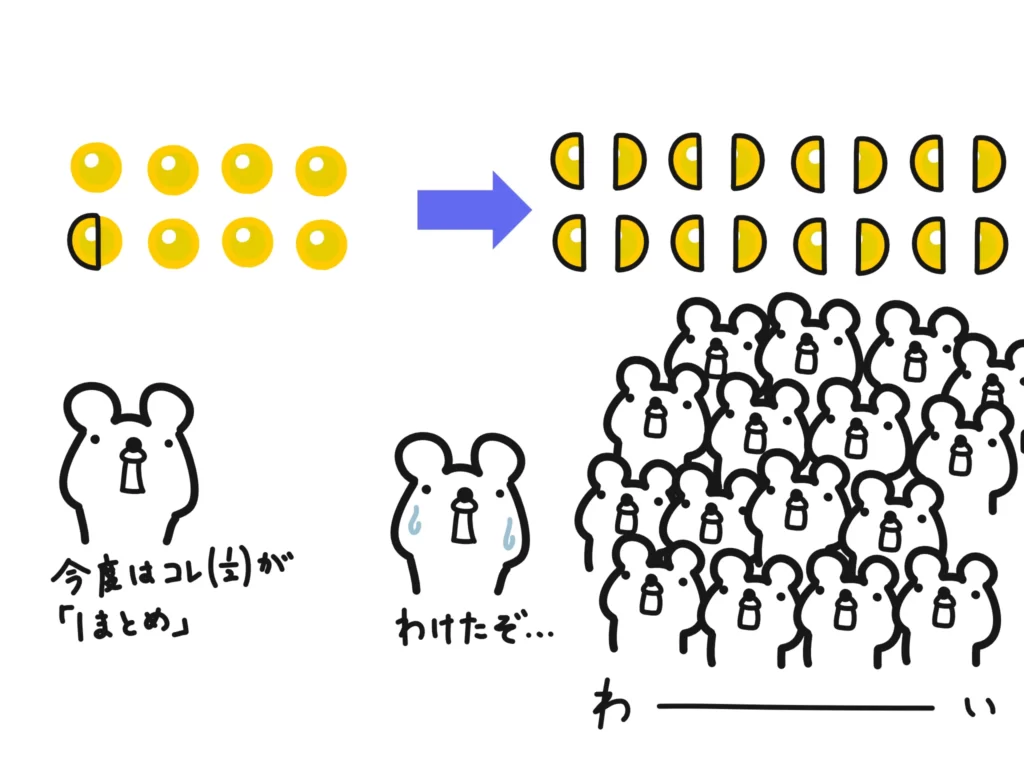

このように「\(\displaystyle \frac{1}{2}\)を1セット」とすると、「8は16セットに分けられる」というのがわかりますね。



なるほど…確かに。「割る数を1まとめとする」と考えたら分数の割り算でもわかりやすいですね。
でも、なんでそれが「逆数を掛ける」という操作になるんですかね?
ここまできていればあと少し。この先は「比」の考え方を使います。
この「割る数を1セットにする」という考え方は「割る数を1セットとしたとき、割られる数は何セットに対応しますか?」ということになるので、実は比の話なんですね。



あとは、次の図を見てくれればわかると思いますよ。

ここでポイントとなるのは、「割る数は必ず1セットにする」という点です。
つまり、比の計算で言うと、「(割る数\(a\))×\(b\)=1(セット)」となる\(b\)を求めたいわけです。
…この\(b\)って、まさに最初に説明した割る数\(a\)の逆数のことですよね?
ということで、割られる数に割る数の逆数\(b\)を掛ければ、欲しい値が得られます。



「割る数を1セット」としたとき「割られる数は何セット?」という、比の計算を簡単にするために逆数を掛けるんですね。
まとめ
意外と説明しづらい「分数で割ること」について、図を使いながら説明しました。
「分数で割るときは逆数を掛ける」…ポイントは割り算のイメージと、比の計算です。
この理由が説明できたらちょっとカッコイイかもしれませんね。









