ドルコスト平均法とは？利点を数学的にわかりやすく説明

「ドルコスト平均法」ご存じですか？

投資に興味のある方なら知っていると思います。いわゆる定額投資、ですね。

さて、このドルコスト平均法、投資でのリスクを減らし長期的に見て利益を生み出しやすい（必ずしもそうとは限りません。投資ですから。）投資法だ、と言われています。

…なぜだか知ってます？

この記事では、ドルコスト平均法がなぜ利益を産みやすい投資法なのか、説明します。

※ あくまで、数学的にドルコスト平均法がなぜ得をするのか、を説明する記事です。投資の利益を保証する内容ではありません。…わかってるとは思いますが。

ドルコスト平均法とは？

ドルコスト平均法とは、簡単に言うと「定額投資」です。毎月（とか毎日・毎年とかは人によるでしょうが）同じ額を投資する、という方法です。

それだけ？と思う方もいるでしょうが、本当にそれだけです。

株の（株とは限りませんが、面倒なのでこの記事では株に投資、ということにしておきます）値動き次第ではありますが、長期的に定額投資を続けると、リスクが減る、という方法なのですが、その理由を数学的に説明します。

定額投資した場合と定量買付した場合

例えば、ある株が次のように値動きしたとしましょう。

１月目	２月目	３月目
150円/株	100円/株	200円/株

値動きが激しい…というのは置いておきましょう。この株に対して、はなこさんと、たろうくんが、それぞれ次のように投資したとしましょう。

投資する金額、取得できる株の数が違うので、平均の取得株価でどちらが得をしたか、を比べてみます。

たろうくんの場合

地道に計算していきましょう。

１月目、200株を買うのに必要な金額は\(150 \times 200 = 30000\)（円）。

２月目、200株を買うのに必要な金額は\(100 \times 200 = 20000\)（円）。

３月目、200株を買うのに必要な金額は\(200 \times 200 = 40000\)（円）。

よって、３ヶ月で投資した金額は\(30000 + 20000 + 40000 = 90000\)（円）、取得した株数は\( 200 \times 3 = 600\)（株）。

なので、平均の取得株価は\(90000 \div 600 = 150\)（円/株）となります。

はなこさんの場合

こちらも地道に計算していきます。

１月目、30,000円で買える株は\(30000 \div 150 = 200\)（株）。

２月目、30,000円で買える株は\(30000 \div 100 = 300\)（株）。

３月目、30,000円で買える株は\(30000 \div 200 = 150\)（株）。

よって、３ヶ月で投資した金額は\(30000 \times 3 = 90000\)（円）、取得した株数は\( 200 + 300 + 150 = 650\)（株）。

なので、平均の取得株価は\(90000 \div 650 = 138.46\)（円/株）となります。

なぜ定額投資の方が得をしたのか？数学的に説明

それは、それぞれの平均の計算方法に秘密があります。

今回、３ヶ月間のトータルの投資金額と取得株価で平均を計算しましたが、各月の平均から取得株価の平均を出すこともできますよね？

たろうくんの場合

定量買付をした、たろうくんの各月の平均取得株価を計算してみましょう。

	１月目	２月目	３月目
投資金額	30,000円	20,000円	40,000円
取得株数	200株	200株	200株
各月の平均取得株価	150円/株	100円/株	200円/株

というか、計算するまでもなく、150円/株→100円/株→200円/株ですよね。当たり前です。

\( ( 150 + 100 + 200) \div 3 = 150 \)（円/株）、となります。

はなこさんの場合

定額投資をした、はなこさんの各月の平均取得株価を計算してみましょう。

	１月目	２月目	３月目
投資金額	30,000円	30,000円	30,000円
取得株数	200株	300株	150株
各月の平均取得株価	150円/株	100円/株	200円/株

残念ながらさっきのは計算間違いではありません。計算間違いをしているのは今のたろうくんです。

でも、「ん？何が間違ってるの？なんでさっきのと差が出るの？」と思った人も多いと思います。

これは、各月の平均取得株価を計算するところまでは合っているんですが、そのあと、全体の平均を出すところが間違ってるからなんですね。

理由は「相加平均」と「調和平均」

こうやって表にまとめてみると、なぜ違いが出たか、ますますわかりませんよね。

たろうくんとはなこさんがそれぞれ各月の平均取得株価を計算して、結果同じ値が出ていますが、実は計算方法が違うのです。

別の記事で説明していますが、

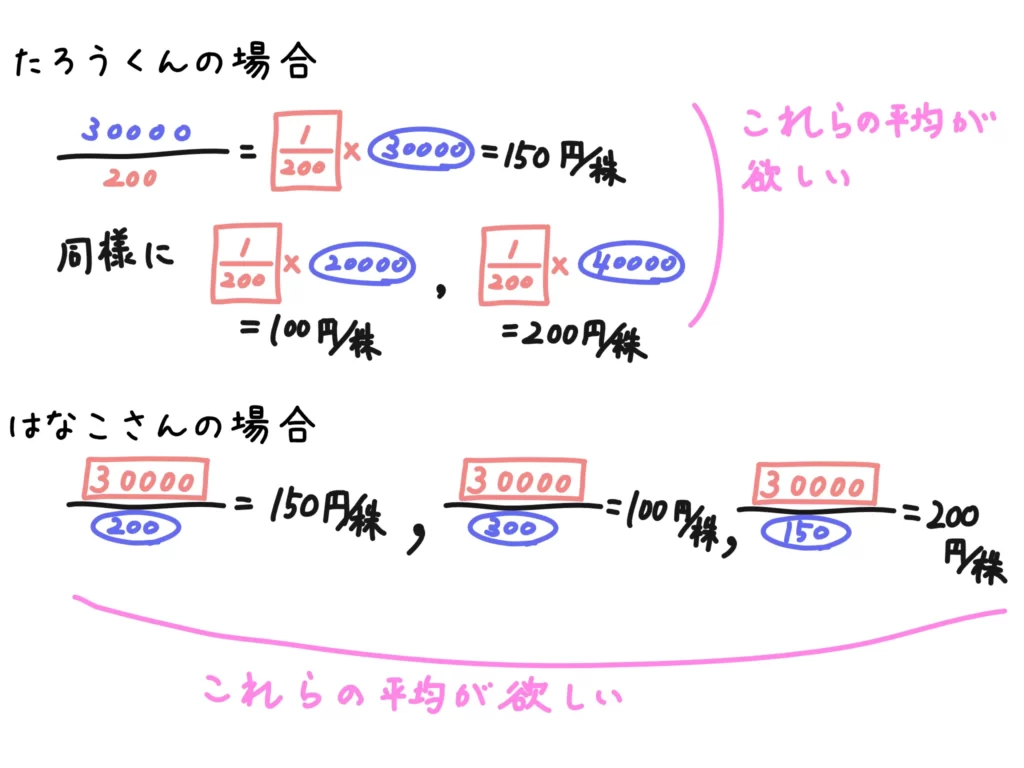
たろうくんの場合、全体の平均をとるときには「相加平均（いわゆる普通の平均）」で計算しなければならなく、

はなこさんの場合、全体の平均をとるのに「調和平均（平均の平均）」で計算しなければいけないのです。

そして、同じ変数で計算すれば、（相加平均）\( \geq \) （調和平均）となることが証明されています。

まとめ

最近は投資をする人も増えているので「ドルコスト平均法が有利らしい」というのは聞いたことがある、という人もいるかと思います。

ですが、「ドルコスト平均法が有利」な理由も、実は数学で説明できます。

今回のように「数学の理論が身近な生活に直接結び付いている」というのは意外と少ない例なので、なかなか面白い話ですね。