PR
三角比とは?その「本質的な利点」をわかりやすく説明
三角比…アレですよ、高校で習ったヤツ。
\( \sin \)、\( \cos \)、\( \tan \)
 たろぅ
たろぅやばい、拒否反応が…。
わかりますよ。まぁ、これこそ高校数学で「なんでそんなもん考えるんだ!」の代表ですから。
ですが、コイツはツールとして非常に優秀なヤツなんです。



ツール?なんのこと?そんなの習わなかったぞ…?
という人がほとんどだと思いますので、この記事では「三角比とはなんぞや?」という目線で話をしていきます。
三角比の定義



三角比の定義は以下の通りになります。



(またこの先生か…。定義とか、そういう難しいこと言うから数学はキライなんだ…。)



うるさいですよ。



(なぜ考えていることがわかる…。)
まずは三角比の定義です。
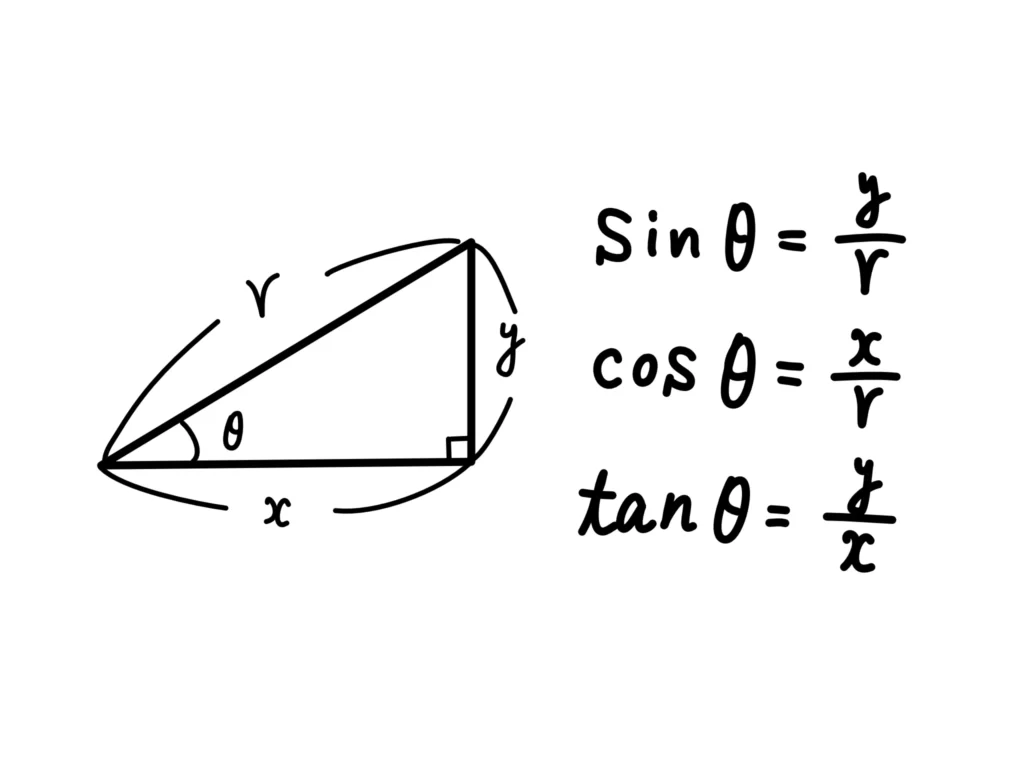
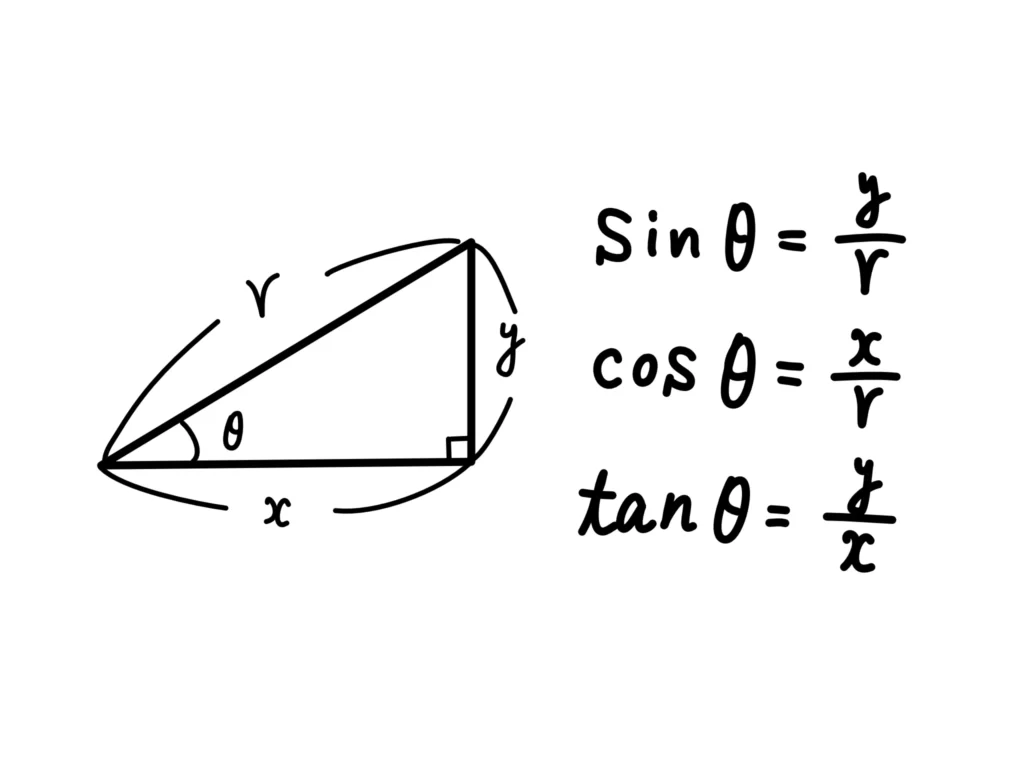
ここから派生する、
- \(y=r\sin{\theta}\)(斜辺と角度で高さがわかる)
- \(x=r\cos{\theta}\)(斜辺と角度で底辺がわかる)
- \(y=x\tan{\theta}\)(底辺と角度で高さがわかる)
これらはよく使う性質なので覚えておいて、さっと使えるようにしておきましょう。特に物理・力学なんかではよく使います。



定義は分かりましたけど、これってなんなんですか?



そうですね。いきなり「これが定義だ」と言われても、「だからなんだ?」という話になりますよね。少しずつ説明していきましょう。
三角比で測ってみよう…なにを?
そうですね、テニスコートに出たとしましょう。



さて、じゃあ、テニスコートに来ました。



あれ?サイドラインがないですよ?



当たり前ですよ。昨日、部活の練習中に切れちゃったんだから。だから、サイドラインの長さを測って張り直してもらいます。




なぜ俺がそんなことを…。



確か…エンドラインは11mだったと思います。サイドラインは何mだったかな…。忘れた。測ってください。



えぇ…。巻尺持ってこなきゃ…。
はい、ストップ。こういうときに三角比が役に立つんですね。



長さを測るのって、正直面倒なんですよね。場合によってはムリです。それに比べて測りやすいのが、角度、です。



まぁ、確かにそうですよね。分度器があれば測ることができます。
ちょっと現実的な話になってしまいますが、長さを測るよりも、角度を測る方がはるかに楽です。
そして、それを元に長さを計算できるのが三角比、というツールなんです。



この場合は\( \tan \)を使えば計算できますね。ココの角度は何度ですか?
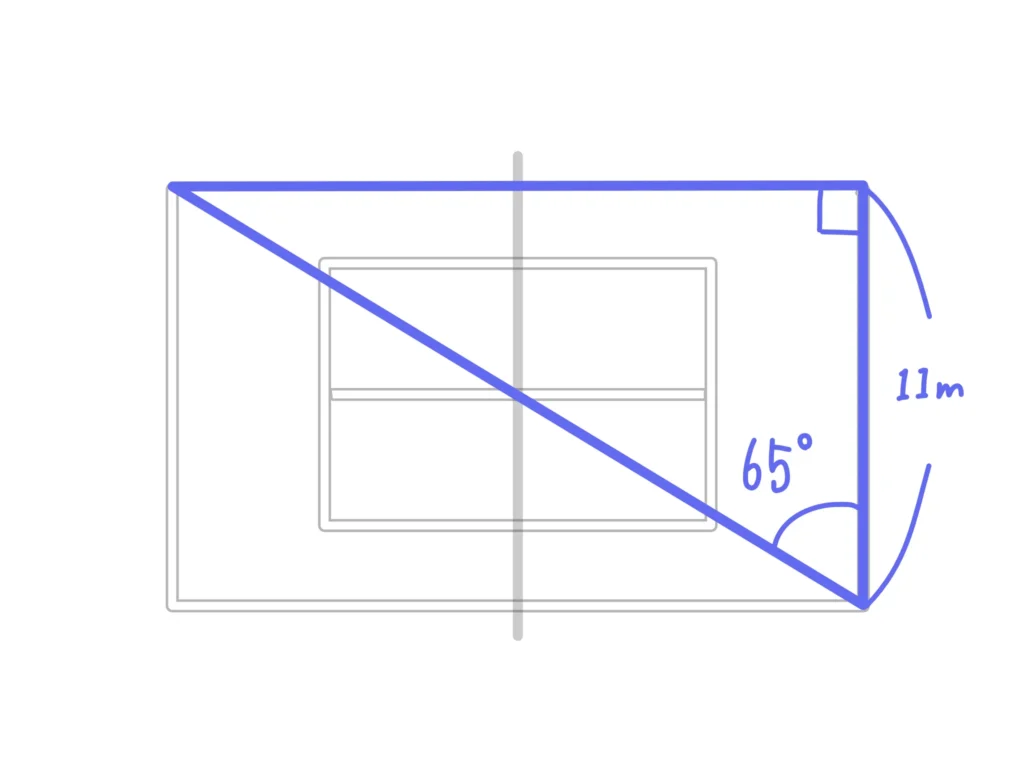




65度…ですかね。



三角比表を使うと、\( \tan(65°) = 2.1445 \)なので、\( 11 \times \tan(65°) = 23.54 \)になりますね。





なるほど、23.54mですね!長さがわかってよかったですね!



いや、今からライン張るんですよ?



…。
※ ちなみに、コートの長さは大体揃えましたが、正規のモノとは若干誤差があります。ご了承ください。
それでも三角比…ちょっと納得いかない



いや、まぁ確かに便利っちゃ便利だけど…。このご時世、長さなんかいくらでも測り方あるじゃない。そもそもテニスコートのサイドラインくらいインターネットで調べれば一瞬で出てくるわ。
ま、こういうところですよね。数学を現実問題と結びつけると逆にツッコミどころが出てきます。
で、数学がキライな生徒が増えると思います。変な所に言い訳をするスキを与えてしまいます。
数学自体は論理に一部のスキもないのに、もったいないです…。
まぁ個人的な意見ですけどね。



じゃあ、三角比の本当に賢い所を教えましょう。
三角比の賢さの正体、それはズバリ「比」です。
模型で考えよう
全然話は変わりますが、例えば模型。模型ってすごくないですか?



あー、よくガン○ムのプラモデル作りますよ。



じゃあ例えば、1/1スケールのガン○ムの模型があったとしましょう。これに色を塗りたいので、どのくらいの塗料が必要か?を考えようとしたとします。



とりあえず、塗料くらいいっぱい買っときましょうよ。



そういう考えがダメなんですね。必要以上の在庫を抱えてどうするんですか?塗料なんかすぐ乾いて使えなくなりますよ?そのムダが会社を倒産の危機に追い込むんですよ?



(なんの会社だよ…)いや、でも計算するの大変じゃないですか。それに、1/1の大きさのものなんか、どう計算すればいいかなんて想像できませんよ…。
こういうときに便利なのが「比」ですよね。
ちなみに気になって調べてみたのですが、プラモデルの「1/〇〇スケール」というのは長さベースのようです。当たり前と言えば当たり前ですが、面積の話をするのでちょっと気になってしまいました。



あ、ハイハイ!!ガン○ムのプラモデルを買ってきて、実際に塗装してみればいいと思います!で、どのくらい塗料を使ったかを量っておいて、スケールを基準に計算すればいいと思います!



まぁ、大体合ってるけど、全部塗るの?



え?そりゃそうでしょ?ガン○ムのプラモ欲しかったんですよ。



目的を忘れないようにね?



…。
実際に数学の問題を解く際にも、目的(=向かうべきゴール、答え)を忘れちゃう人って結構いるんですよね。
目的を忘れないでください。逆に目的をしっかり押さえていれば本当にその方法が必要なのか?の判断ができます。



今回も、そんな全部を塗る必要ありませんよね?わかりやすく、ちょっとの面積だけ塗るなりして実験して、そこから計算すればよくないですか?



まぁ、そうですけど…。



そもそもちっちゃいプラモデルに一生懸命塗った塗料を量って、大きいスケールに換算するんですか?面倒でしょ?
そんなのより、プラモデルでなくても、何かに1㎠だけ塗って、それに必要な塗料の量を量ってから、本当にいる量を計算する、とかした方がわかりやすくないですか?



そうすね。1/1の方に塗ることができればいいですからね…。
全然関係ないように見えますが、実はこの考え方が三角比が便利である理由なんです。
三角比は規格化した値
三角比の値は角度によって決まっています。
で、この値は後ほど単位円を使った三角関数の定義によって拡張されますが、重要なことは、
\( \sin \)、\( \cos \)は直角三角形の斜辺を1として、高さ、底辺がどのくらいになるか?
\( \tan \)は直角三角形の底辺を1として、高さがどのくらいになるか?
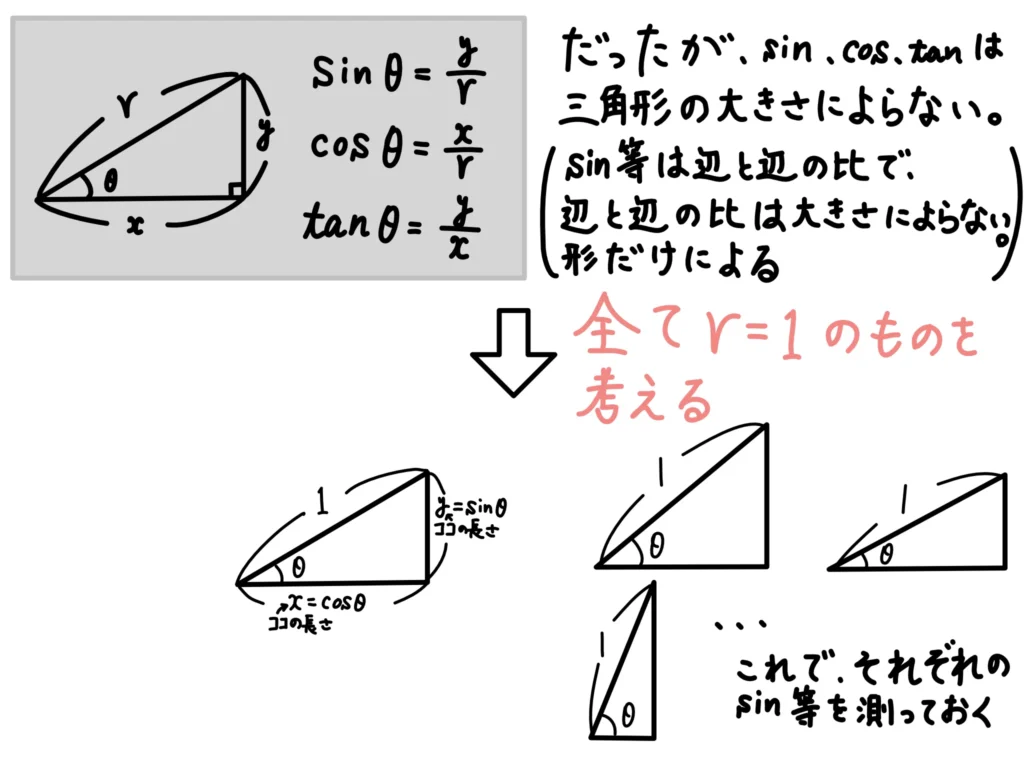

を規格化して表したもの、と思ってくれればOKです。



ちなみに三角比に対して「規格化」という言葉はあまり使いませんが、ベクトルや統計では「規格化・正規化」という言葉をよく使います。
要は、他でも扱いやすいようにわかりやすい値(通常は1)を基準に揃えるという操作です。
1を基準とした値は扱いやすいんです。「2」と言われれば2倍すればいいだけですし、「100」と言われれば100倍すればいいだけです。
ということは、例えば「斜辺の長さ10」と言われたら、\( \sin \)、\( \cos \)の値を10倍すれば、高さ、底辺が出ませんか?
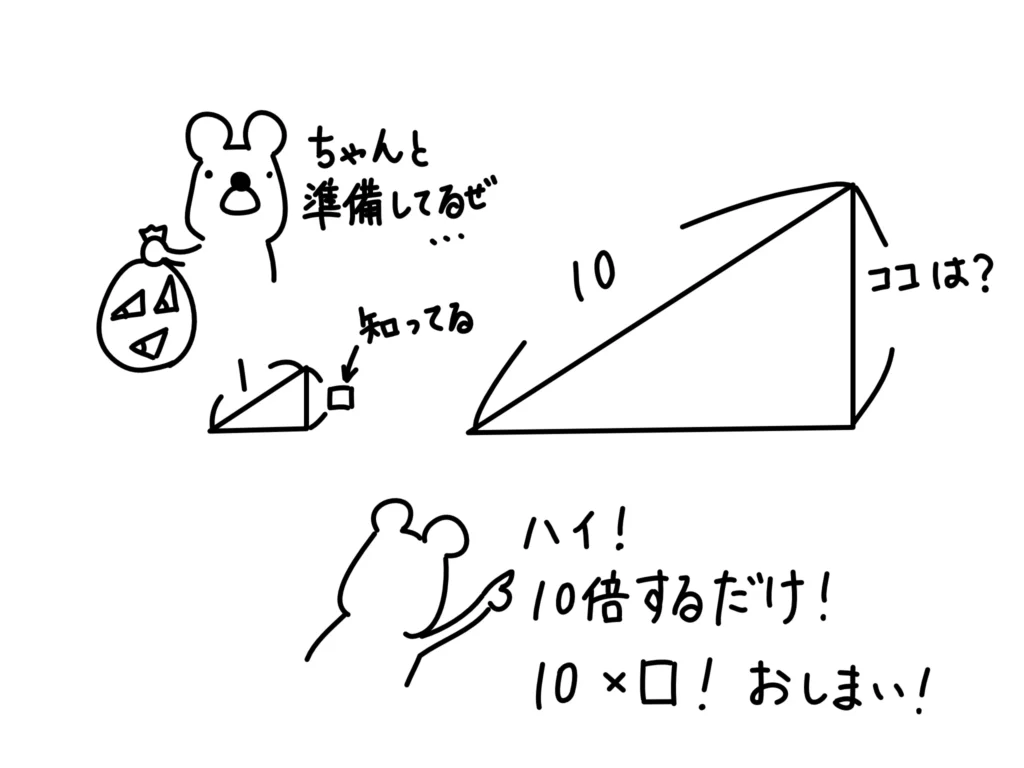




…なるほど。三角比って、1を基準としたものをあらかじめ値として持っておくことで、他の大きさで使いやすくしてるんだ…。



その通り!もちろんそれだけでなく、そこから派生する公式も便利なものばかりだし、三角比を拡張した三角関数は回転や波を表現するときに必ず出てくるツールなんです。



なるほど…。三角比って一見何をしているかわかりにくいですが、1を基準とした値で考た、物差しみたいなものなんですね。で、それが便利なツールに発展していく、ということですね。
まとめ
途中、小話を挟んでしまったので、ちょっと長くなってしまいました。
高校生の頃に習って、意味もわからず公式を覚えさせられてイヤになった三角比を、ちょっとでも理解していただけたら嬉しいです。
三角比が賢い理由(規格化)も、現実世界では結構使いますね。4人前の料理のレシピよりも、1人前のレシピを知っていた方が、何人前でも必要量を計算しやすいのと同じ理由です。
このように、数学の本質部分は実生活でも役に立つので、数学を勉強しながら本質部分の獲得を目指していきましょう!







