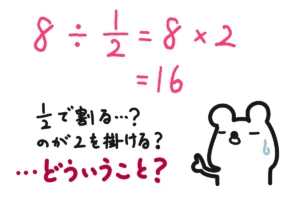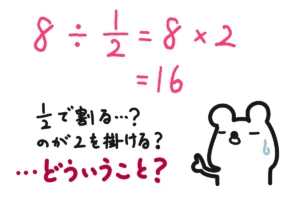PR
マイナス×マイナス=プラス?をわかりやすく説明!
マイナス×マイナス=プラス
まぁ、そうですよね。中学のときに習いましたもん。
では聞きますが「なぜマイナス×マイナス=プラスになるのでしょう?」
 たろぅ
たろぅいや、なぜって言われても…。改めて聞かれると…。
この質問に3人の先生が答えてくれるようです。



お願いします。
ちょっと弁が立つ先生



「マイナス」ってどんなイメージかな?



え?数学の話じゃなくて、ですか?
みなさん「マイナス」と聞くとどんなイメージですか?
「マイナスポイント」「マイナス成長」「マイナス効果」…。



なんかネガティブなイメージですよね。



そうですね。ちなみに英語で「マイナス」のことをなんて言うか知ってますか?



…え?「マイナス」じゃないんですか?



「マイナス(minus)」という場合もあるけど、特に「負の値」という意味では「ネガティブ(negative)」を使うんですよ。



なるほど!
マイナスにはネガティブなイメージがあります。そして、掛け算には「それがいくつかある」というイメージがあります。



ネガティブなものがいくつもあったら…。



そりゃ、大ネガティブですね。
では、ネガティブなものが「マイナス個あったら?」



なんかプラスに転じそうですね。



そうでしょ?債権を譲渡すれば、資金はプラスに転じますよね?マイナス分が無くなるわけですから。ということで、「マイナス×マイナス=プラス」なんですよ。



なるほど…そう言われれば。(あんまり数学関係ない気がするけど)
マイナス=ネガティブ、マイナス=反対向き、という感覚を二つ組み合わせれば、日本語レベルでなんとなく納得がいきますよね。
中堅中学数学先生



数直線ってわかりますか?



数直線ってあれでしょ?線かいて、矢印書いて、その上にポイント打って「ここが2だ!」ってやる、あれでしょ?



そうですね。数直線を使って説明してみましょう。
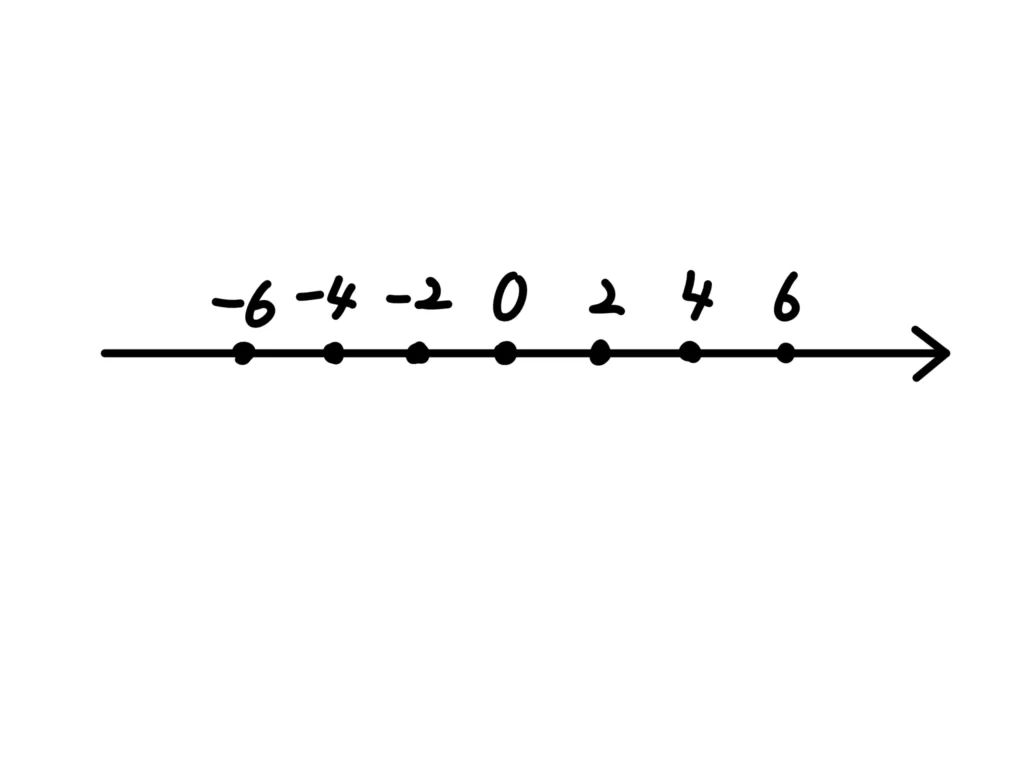




ここで、プラスの掛け算を見てみましょう。
\( 2 \times 1 = 2 \)、\( 2 \times 2 = 4 \)、\( 2 \times 3 = 6 \)ですよね。



はい、その通りです。(当たり前だろ)



今「当たり前」って思いませんでした?



…いいえ。



とにかく、プラスの数に、掛ける数を増やせば、+2されますよね?



まぁ、そうですね。



逆に掛ける数を減らしていけば、ー2される、とも見えますよね?



確かに。
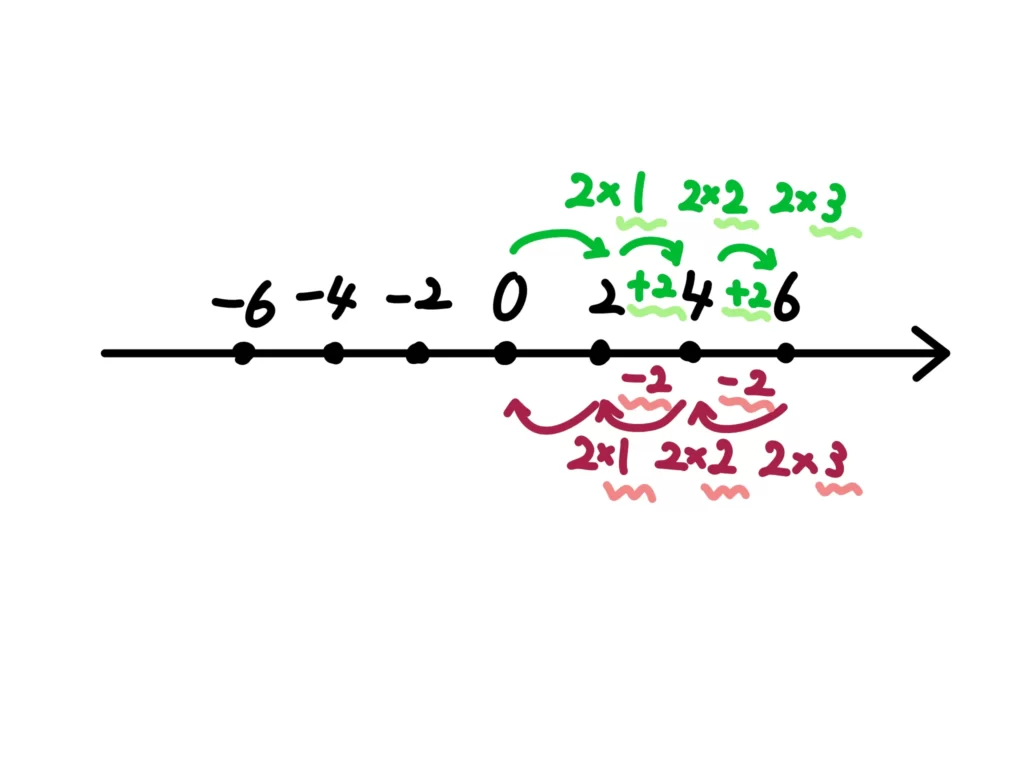




ということは、この調子で掛ける数を減らしていけば、\( 2 \times 0 = 0 \)、\( 2 \times (-1) = -2 \)、となりますよね。



なるほど。
これをマイナスの数に掛ける数を増やせば、減らせば、と考えます。



マイナスの数の場合は、\( (-2) \times 1 = -2 \)、\( (-2) \times 2 = -4 \)、\( (-2) \times 3 = -6 \)となり、掛ける数を増やせば−2されていますよね?逆に言うと…。



掛ける数を減らせば、+2される、ってことですか?



そういうことですね。ということは、\( (-2) \times 0 = 0 \)だし、\( (-2) \times (-1) = \cdots \)



なるほど、\( (-2) \times (-1) = 2 \)になりますね。
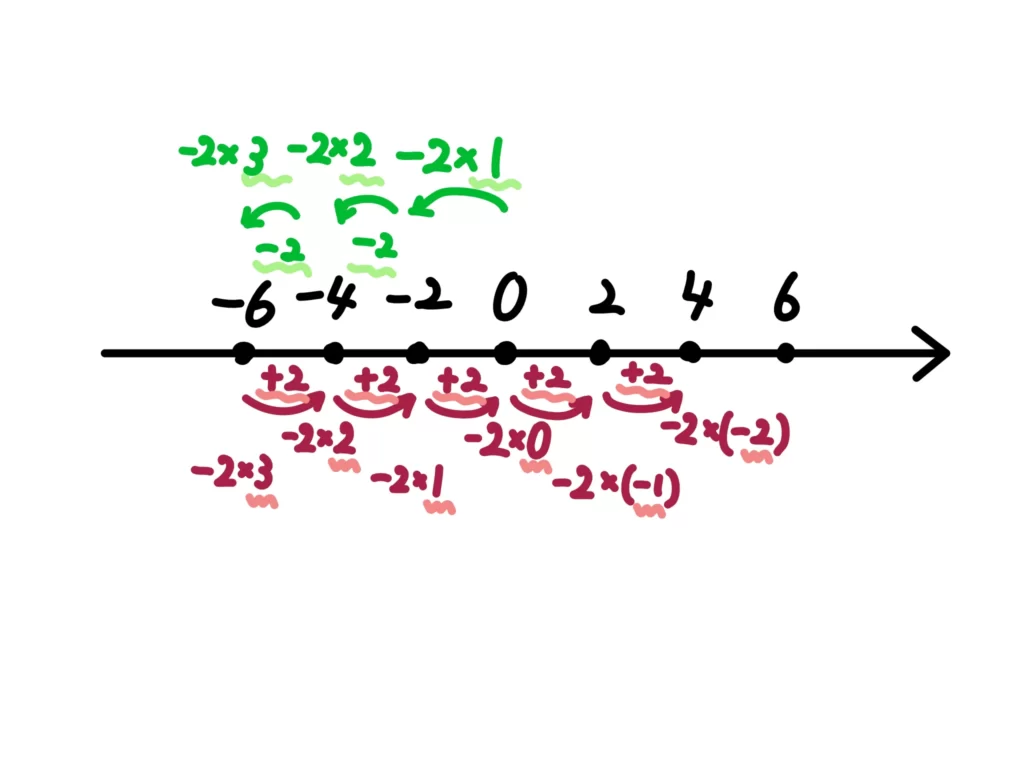




その通り!
なんとなくわかりやすいんじゃないでしょうか?
特に重要なポイントは、「法則性を見出して、それを足がかりにする」という考え方をしている点です。
世の中は、実はあまり原因なく物事が動くことがないです。なにが起きるにしても大体原因があります。
法則性を見出す、ということは原因に沿って物事を捉える、ということです。そして、それを足がかりに物事を考えれば、大体予想通りの結果が得られます。
だって原因があるんだから。
「ヒヤリハット」とかも一緒ですよね。1件の重大事故の裏には、29件の軽い事故があり、300件の未遂事故がある、っていうアレです。
アレも、結果だけ追うと「重大事故」「軽い事故」「未遂事故」となりますが、原因は同じです。
「未遂」のうちに法則性を見出せば、その先の「重大事故」を防ぐ余裕は十分にあります。
ガチンコ数学教師



君は分配法則を知っているかね?



えっ…?式を展開とかするときのアレですか?



その通りだ。では、ある値\(a\)(ただし\(a\)は正の数とする)に対する負の数\(-a\)の定義を述べたまえ。



え…?負の数?定義?(なんかこの先生こえぇな)



ふぅ、やれやれ。いいか?マイナス×マイナスがプラスになる理屈は、この分配法則と負の数の定義によって説明できるのだよ。



…。(早く終わらねぇかな)
最後は少し数学っぽく説明をします。
とはいえ、「分配法則」がわかっていれば比較的理解しやすいかな、と思います。
分配法則とは\( a \times (b+c)=a \times b + a \times c \)と計算できる、という法則のことです。
やりましたよね、\( 2 \times (x^2+3x)=2x^2 + 6x \)みたいな式計算。アレです。
また、先生の言う\(-a\)の定義とは、\(a\)に対して、\(a+b=0\)となる\(b\)のことを\(b=-a\)といいましょう、ということですね。



\(a+b=0\)のとき、\(b=-a\)と考えれば、確かに\(a+(-a)=0\)となって、\(a\)に対する\(-a\)の定義になりそうです。
これにもうひとつ補足の考え方として「引き算はー(マイナス)の足し算」であることと「\(-a = (-1) \times a \)」となることは認めます。
ex1. \( 5-2 = 5+(-2)=3 \)
ex2. \( -2 = (-1) \times 2 \)



ここまではいいですか?



はーい。
では、本題です。



突然ですが、\( (-a)(-b)-ab \)という式の値がどうなるか、先ほどの分配法則を使って考えてみましょう。



?
先ほどの補足の考え方を用いると、\( (-a)(-b)-ab = (-a) \times (-b) +(-a) \times b \)となるのはわかると思います。



ここでポイント!先ほどの分配法則を逆に使ってやるのです!
いわゆる「くくる」という操作ですね。\( (-a) \times (-b) +(-a) \times b \)には共通因数\( (-a) \)があるので、分配法則を逆に使って「くくる」という操作ができます。
ということで、先ほどの計算を進めると、こんな感じになります。
\( (-a)(-b)-ab = (-a) \times (-b) +(-a) \times b = (-a) \times (-b+b) = (-a) \times 0 = 0 \)



つまり、\( (-a)(-b)-ab = 0 \)という等式が出来上がります。



なるほど。
ここまでくればあと一息。\( (-a)(-b)-ab = 0 \)の両辺に\( ab \)を足してやると…。



あ…。\( (-a)(-b) = ab \)って式ができた。



これでマイナス×マイナス=プラス、というよりも\( (-a)(-b) \)のマイナス同士は打ち消し合うことが示されましたね。でもまぁ、およそ言いたいことは同じですけどね。



なるほど!(意外とわかったぞ。)
基本的な式変形を論理で組み上げていって新しい考え方をつくる、という点がポイントです。
重要なことは、論理のみで組み上げたものは次のステップでも揺るぎない、ということです。
これは特に新しい事業を始めたり、プログラミングとかでも重要な考え方ですね。実際に私もプログラミングをするので、こういう数学的なプロセスは結構役に立っています。実はプログラミングで重要な数学的考え方が他にもあるんですが…それはまた別の機会にしましょう。
なるべく主観を捨てて、論理だけで組み上げれば、自ずと答えが見えてくる。これが論理の力ですね。
また、途中で「分配法則」を逆の方向に見て「くくる」という操作をしています。
物事を色々な方向から見るのは重要ですね。新たな気づきが得られます。
まとめ
いかがだったでしょうか?意外と説明できないマイナス×マイナス=プラス。考えてみると面白いですよね。
このくらいのペースで、数学に関するちょっとした疑問を学び直していきたいと思います。
また、こちらでも話した通り、「数学がなぜ役に立つのか?」というのは、こんな感じで記事の中で説明していきます。