平均の種類・求め方、いくつ知ってる？

平均、と聞いたら、皆さん何を思い浮かべますか？

ちなみに、どうでもいいですが令和３年の統計によると、サラリーマン（男性）の平均年収は約546万円らしいですよ。

この平均を見たとき「高い！」と思いますか？それとも「まぁ、それなりだな」と思いますか？

これがよく言われる平均のマジックですね。恐らく、大体の人が「いや…そんなに貰ってない」と思うでしょう。

これは一部の給料の高い人によって平均が釣り上げられているからですね。こういう、一般的でない値を「外れ値」といいますが、平均はこの外れ値の影響を受けやすいんです。統計の話になりますが。

話が逸れましたが、皆さん、この平均は色々な種類があるのを知っていますか？

この記事では「色々な平均」について話をしていきます。

どんな「平均」が適切？

普通の平均「相加平均」

正解です。いわゆる普通の平均ですね。算術平均とか相加平均とか言ったりもします。

「全部足して、その足した数で割る」という計算方法です。特に難しいことはないと思います。

割合の平均「相乗平均」

え？と思った人もいると思いますが、こういうときの平均の出し方はちょっと違うんですね。

得点の推移を追っていくと、100点→75点→61点→73点になっていますが、「最初の100点から最後の73点を、伸び率を使って計算」しようとすると、以下のようになります。

\( 100 \times 0.75\times 0.81\times 1.2 =72.9 \)
※1 今回は話を簡単にするために四捨五入して73点、とします。
※2 ちなみに伸び率を掛ければ次の点数になります。例えば2回目から3回目の点を出すには2回目の点数75点に伸び率81%、つまり0.81を掛けて、\( 75 \times 0.81 = 60.75（61点） \)とすれば計算できます。なので、上記のようにどんどん伸び率を掛ける計算になります。

\( 100 \times 0.92\times 0.92\times 0.92 =77.8 \)

このように、普通に平均（相加平均）をとってしまうと平均の意味からずれた値がとれてしまいます。

これは、前の値に割合を掛けて次の点数を計算しているからですね。こういった感じで、掛けていくモノの平均を足して出す、というのは違和感を感じませんか？

こういうときには相乗平均（幾何平均）という方法で平均を計算します。

\( \sqrt[3]{ 0.75 \cdot 0.81 \cdot 1.2 } = 0.9\)

\( 100 \times 0.9\times 0.9\times 0.9 =72.9 \)

前回比のように、何かを掛けて次の値を出すような場合「平均どれだけ掛ければよいか？」は相乗平均を使う、と思っておいてください。

平均の平均「調和平均」

では、実際にどのように計算をすべきかというと、「トータルの距離」「トータルの時間」で平均速度を計算する、という方法が妥当でしょう。

小学生のときに速さの勉強したときに覚えた「き・は・じ」（「み・は・じ」とか色々な言い方で習ったと思います。距離・速さ・時間を計算するアレです。）で時間を計算すると、

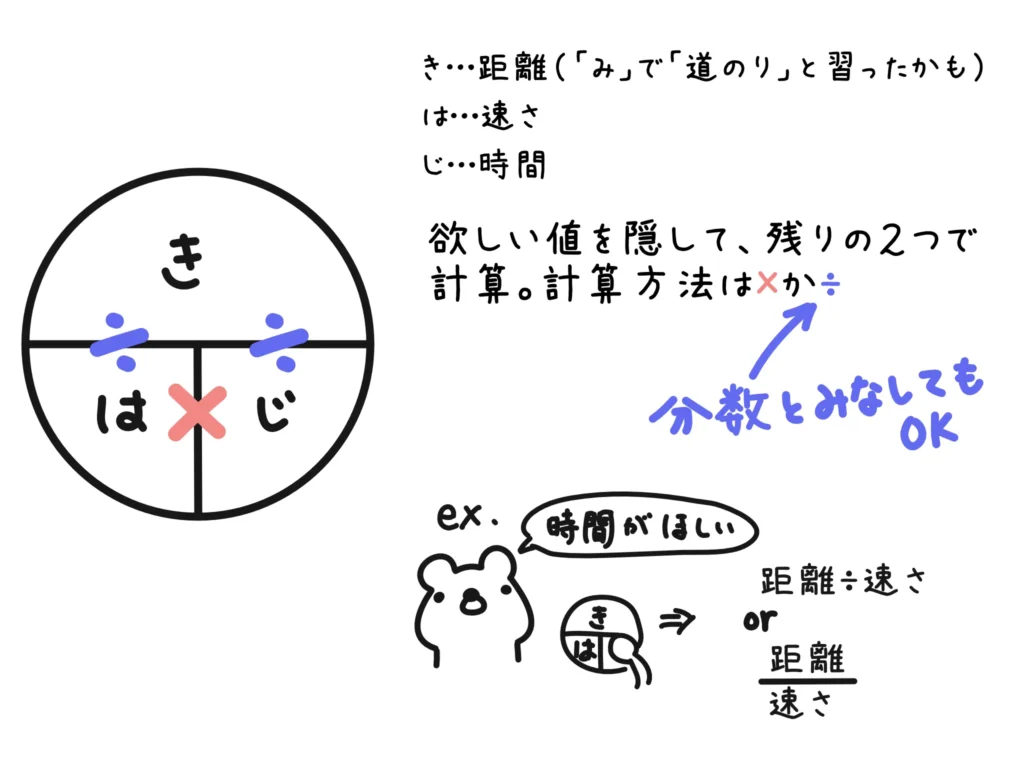
１周目は\( \displaystyle \frac{a}{3} \)(h)、２周目は\( \displaystyle \frac{a}{4} \)(h)、３周目は\( \displaystyle \frac{a}{6} \)(h)です。

距離は３周トータルで\(a+a+a\)ですよね。

なので、平均の速さを計算すると、

このように、一定距離で速度が変わったときに平均を取る場合、調和平均、というもので計算します。上記の計算方法がまさに調和平均です。

先ほどの計算も、いきなり「一定距離の速度の平均は調和平均だ！」ということで、

\( \displaystyle \frac{3}{\frac{1}{3} + \frac{1}{4} +\frac{1}{6}} \) という計算をしてもOKです。

相加平均・相乗平均・調和平均の使い分け

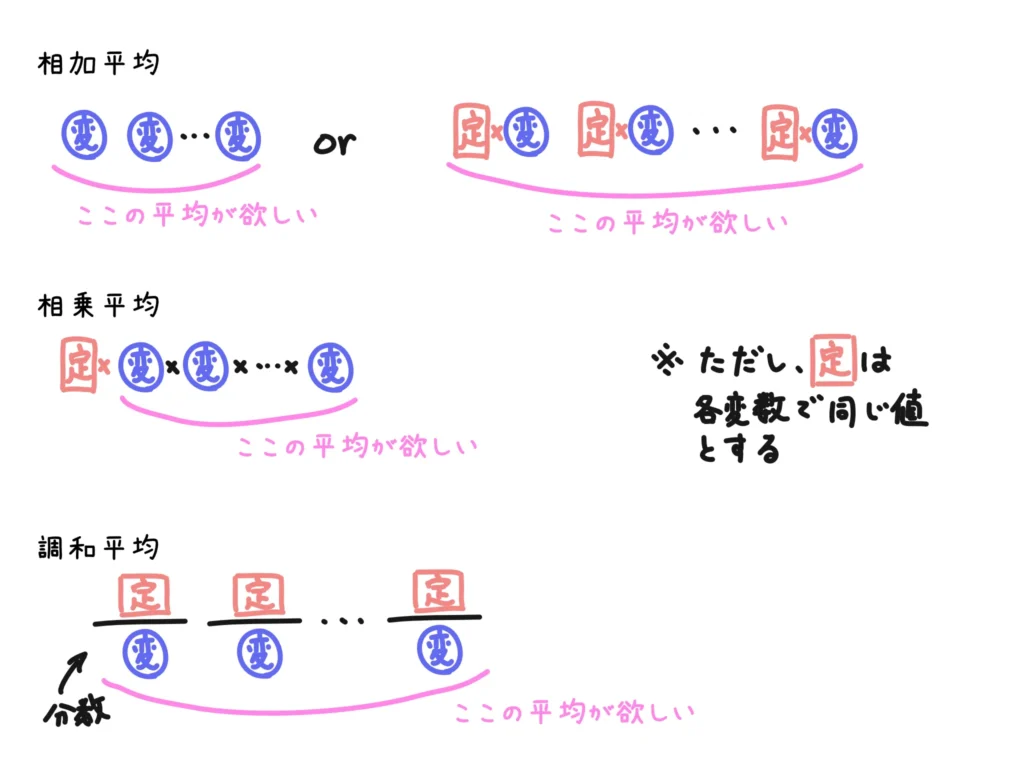
大体の場合は相加平均（普通の平均）で大丈夫だ、というのがわかると思いますが、以下のケースでは注意が必要です。

• 成長率、増加率など、前の値に何かを掛けて次の値を出すモノの平均→相乗平均
• 一定距離における速度の平均、定額投資など、一定の値を何かで割っているモノの平均→調和平均

おまけ「相加・相乗・調和平均の大小関係」

一般的に、同じ変数\( a_1 , a_2 \cdots, a_n \)を使ったときの相加・相乗・調和平均の大小関係は次のようになります。

（相加平均）\( \geq \) （相乗平均）\( \geq \) （調和平均）

なぜこうなるのか、については結構色々な話ができるので、こちらをご覧ください。

まとめ

一口に「平均」と言っても色々な種類があるのがわかったと思います。

相乗平均、調和平均についてはあまり聞き慣れないかもしれませんが、知っておかないと間違いやすいかな、と思います。

調和平均に関しては、実用的な例もありますので、こちらも参考にしてください。