自然対数の底e（ネイピア数）とは？意外と身近な無理数

2023年1月5日2023年7月30日

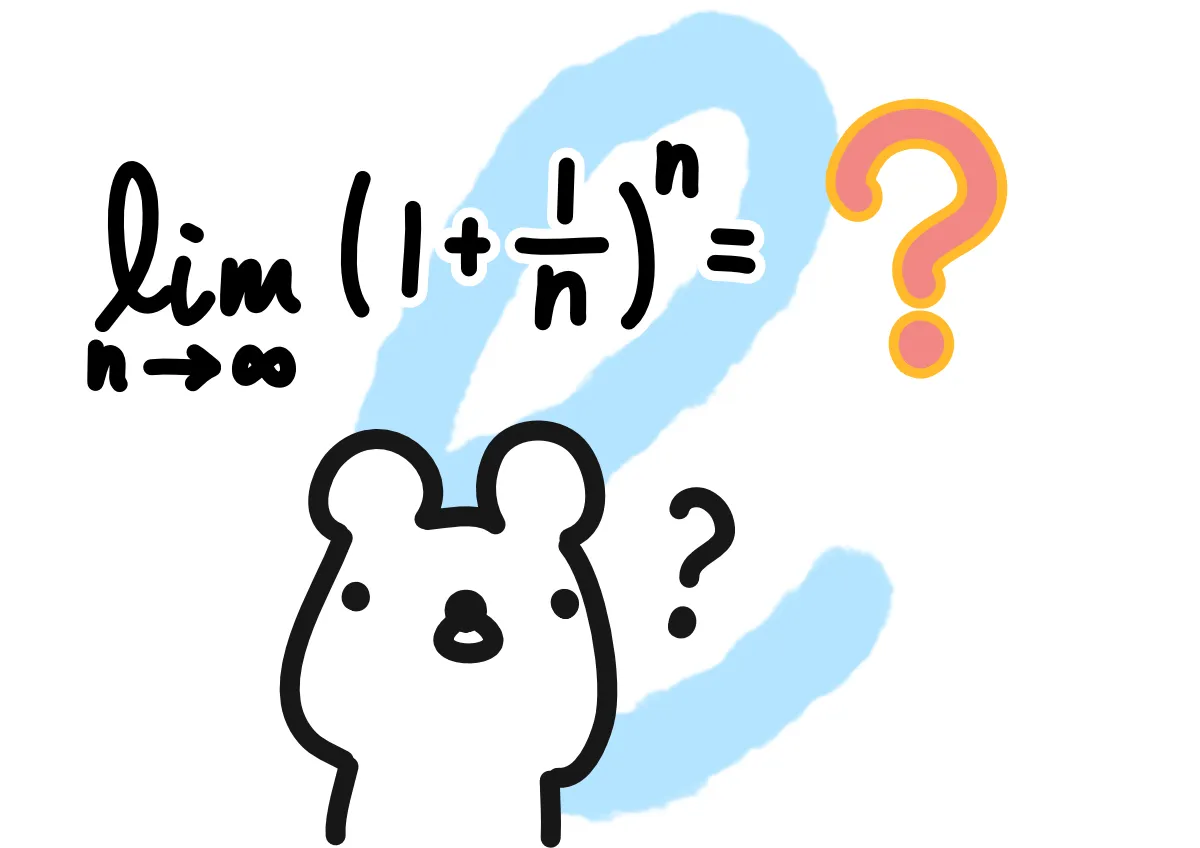
自然対数の底\(e\)…「数学B 確率統計」、「数学III 微分」の分野で「こういう値がありますよ」と紹介される超越数（無理数の中でも代数方程式の解にならない数）です。

特に「数学B 確率統計」では、正規分布が出てきたときに、

「\(e\)は自然対数の底といわれる無理数で、\(e =2.718281828 \cdots\)」

とイキナリ紹介されていて、

たろぅ

（？）

となる人もいるかと思います。

自然対数の底\(e\)（ネイピア数）は円周率\(\pi\)などに比べると、意味がちょっとわかりにくい超越数です。

そんな不思議な自然対数の底\(e\)について色々と掘り下げていきましょう！

このブログで活躍してるクマのLINEスタンプもあります！

意外と身近にあったりする自然対数の底e

たろぅ

いやいや、絶対１回は当たるって。

はなこ

んー…意外と当たらない気がするけど…。

せんせ

ん？どうかしました？

たろぅ

いや、ここに\(\displaystyle \frac{1}{10}\)で当たるクジがある（何回引いても当たる確率は\(\displaystyle \frac{1}{10}\)、何度でも当たる）んですけど、これ、１０回引いたら１回は当たりますよね？

はなこ

いやぁ…結構当たらない気がするんだけど…。

たろぅ

だって、ここで勉強したけど、期待値は\(10 \times \displaystyle \frac{1}{10}=1\)じゃない。絶対１回は当たるって。よし、１０回クジ引くぞ！

せんせ

ちなみに何か景品でもあるんですか？

たろぅ

１０００円相当のガチャガチャが当たるんですよ！１回クジ引くのに１００円かかりますけど！

せんせ

（普通にガチャガチャやった方がいいんじゃないか？）

まぁ今回のクジ、早めに当たれば、また何回か当たれば得をしますけどね…。

さて、ではこのクジ、たろうくんが１０回引いたとき全く当たらない確率を求めてみましょう。

たろぅ

え…やる前から、そんな不吉な…。

１回のクジで当たらない確率は\(\displaystyle \left(1-\frac{1}{10} \right)\)です。

これが１０回続くので、\(\displaystyle \left(1-\frac{1}{10} \right)^{10}\)となります。

これをこちらの関数電卓（外部リンクです）で計算すると、\(\displaystyle \left(1-\frac{1}{10} \right)^{10}=0.3486\cdots\)になります。

たろぅ

あれ？意外と高い？何も当たらない確率ってこんなに高くなるの？

期待値、というのは平均のことですからね。今回のクジは最悪全く当たらないこともあるし、運が良ければ１０回当たることもあるわけです。期待値はその平均をとった値ですから、「期待値（＝平均）１」だからといって「少なくとも１回当たるかどうか？」とは別の話です。

これと同じことをもう少し大きな数でやってみます。

つまり、「\(\displaystyle \frac{1}{100}\)で当たるクジを100回」「\(\displaystyle \frac{1}{1000}\)で当たるクジを1000回」…と、当たる確率を下げて、その分引く回数を増やす、という計算をしてみます。

先ほどの関数電卓を使って計算すると、

\(\displaystyle \left(1-\frac{1}{100} \right)^{100}=0.3660\cdots\)

\(\displaystyle \left(1-\frac{1}{1000} \right)^{1000}=0.3676\cdots\)

\(\displaystyle \left(1-\frac{1}{10000} \right)^{10000}=0.3678\cdots\)

\(\displaystyle \left(1-\frac{1}{100000} \right)^{100000}=0.3678\cdots\)

と、ある値に近づいているように見えます。

結論をいうと、この値は\(\displaystyle \frac{1}{e}\)に近づいていきます。

せんせ

確率・統計ではちょっとしたところに自然対数の底\(e\)が出てきます。
「ものすごく大きいサンプル数」とか「ものすごく短い時間で起きる確率」なんかは極限とも結びつきやすいです。

自然対数の底eの定義

極限による自然対数の底eの定義

自然対数の底\(e\)の定義は、微分の基本のところで話をした極限を使って定義されます。

微分による自然対数の底eによる定義

「微分しても形が変わらない指数関数\(f(x)=a^x\)」を考え、このときの指数関数の底を\(e\)と定める、というスタンスでも自然対数の底\(e\)を定義することができます。

\(f(x)=a^x\)を定義に従って微分すると、（微分の定義はこちら）

\(\displaystyle f’(x)=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} = \lim_{h \to 0} \frac{a^{x+h}-a^x}{h}\)

\(\displaystyle \quad = \lim_{h \to 0} \frac{a^x \cdot a^h-a^x}{h}= a^x\lim_{h \to 0} \frac{a^h-1}{h}\)

これが\(a^x\)になればいいので、

\(\displaystyle a^x\lim_{h \to 0} \frac{a^h-1}{h}=a^x\)

つまり、\(\displaystyle \lim_{h \to 0} \frac{a^h-1}{h}=1\)となるような底\(a\)を\(e\)と定めよう、ということです。

\(\displaystyle \lim_{h \to 0} \frac{e^h-1}{h}=1\)

微分による自然対数の底\(e\)の定義

\(\displaystyle \lim_{h \to 0} \frac{e^h-1}{h}=1\)

\(f(x)=e^x\)とおくと、分子の\(1=e^0\)とみなすことで、微分係数の定義に帰着することができます。

\(\displaystyle \lim_{h \to 0} \frac{e^h-e^0}{h}=\lim_{h \to 0} \frac{e^{0+h}-e^0}{h}=f’(0)=1\)

ちなみに先ほどのクジに出てくる自然対数の底eは？

先ほどのクジの話を一般化すると次のようになります。

当たる確率\(\displaystyle \frac{1}{n}\)のクジを\(n\)回引いて一度も当たらない確率は\(n \rightarrow \infty\)にしたときにどうなるか？

一度のクジで当たらない確率は\(\displaystyle \left( 1-\frac{1}{n} \right)\)なので、\(n\)回引いて一度も当たらない確率は

\(\displaystyle \left( 1-\frac{1}{n} \right)^n\)

\(n \rightarrow \infty\)にしたとき、

\(\displaystyle \lim_{n \to \infty}\left( 1-\frac{1}{n} \right)^n=\lim_{n \to \infty}\left\{ \left( 1+\frac{1}{-n} \right)^{-n} \right\}^{-1}\)

\(-n =k\)とおくと、\(n \rightarrow \infty\)のとき\(k \rightarrow -\infty\)なので、上記の値は

\(\displaystyle \lim_{n \to \infty}\left\{ \left( 1+\frac{1}{-n} \right)^{-n} \right\}^{-1}=\lim_{k \to -\infty}\left\{ \left( 1+\frac{1}{k} \right)^k \right\}^{-1}=e^{-1}=\frac{1}{e}\)

まとめ

自然対数の底\(e\)は、最初ちょっとわかりにくいのですが、高校数学でいえば統計や微分・積分の分野でよく出てきます。

統計や微分・積分の勉強を進めていくにつれ、それこそ自然に\(e\)を使っていくようになり、そのうち自然対数の底\(e\)が無いと話がしにくい、という感じになっていきます。

他にも沢山の分野に顔を出してくる\(e\)。定義を押さえることも重要ですが、逆に、様々なアプローチからその\(e\)の定義に帰着され、結果その値\(e\)を使うのが便利だ、ということを覚えておいてください。

このブログで活躍している「クマ」のLINEスタンプもあるよ！ぜひ見てください！