PR
ベクトルの外積って？高校範囲でも使えるの？【この公式、結構使えます】
ベクトルの積には内積の他に外積（ベクトル積）があるのをご存知ですか？
「知ってる！」「聞いたことある」「初耳」…高校まででは基本的に外積を教えることはありません。もしかしたら「内積の計算は『\(\cdot\)』を書くんだよ〜。この『\(\cdot\)』は省略もできないし、『\(\times\)』とも書けないんだよ〜。『\(\times\)』は外積って言って別の計算の意味だからねぇ」とか聞いたことがあるかもしれません。
この記事では外積について詳しく説明していきます。「高校レベルで外積なんか使えるの？」と思うかもしれませんが、意外と使えるやつなんです。
せんせ特に座標空間の面積や体積計算に上手く使うことができます。
目次
外積って？
はなこんー…困ったわね…。
たろぅん？はなこさん、どうしたの？
はなこ生徒会室片付けてたんだけど、この棚…古いから捨てようと思ってるんだよねぇ…。
たろぅうん、それで？
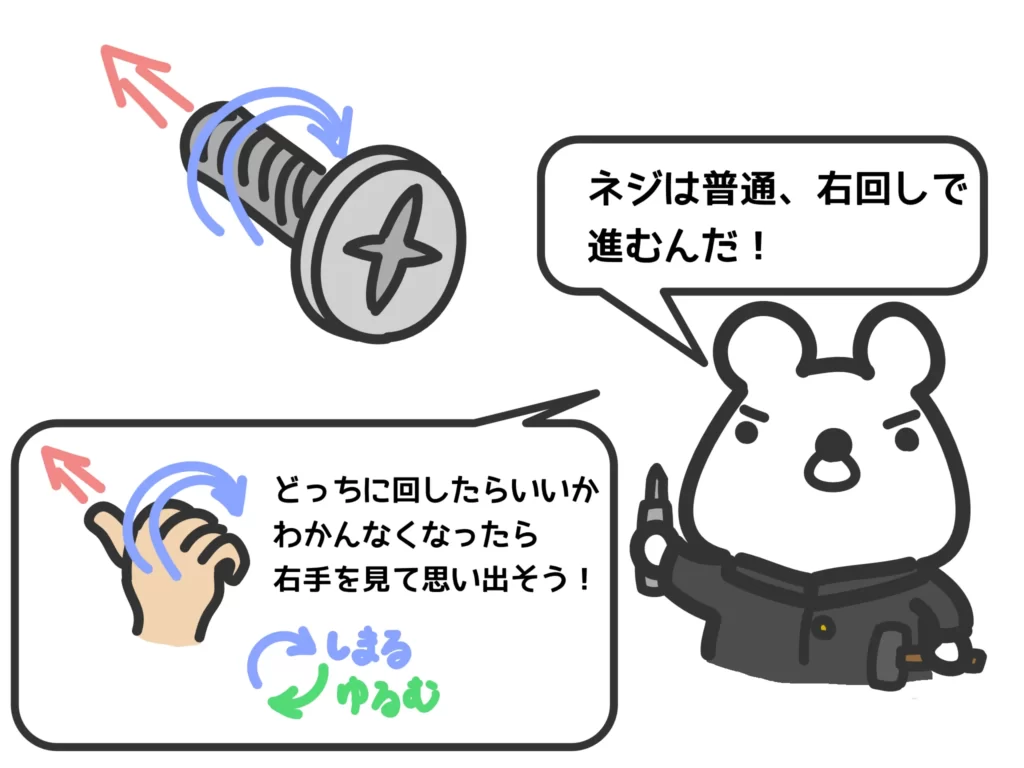
はなこ解体しようと思ったんだけど、ネジが錆び付いてて回らなくて…。
たろぅふっふっふ…そんなときはコレ！ショックドライバー！！
これをネジにあてがって…このハンマーで叩くと…！
（ガンッ！ガンッ！）
あら不思議！錆び付いたネジも取れるのです！！
はなこ（コイツ、いつも工具持ち歩いてんのかしら…）
わぁ！ありがとう！！ついでに、ゴミ捨て場に持っていっといてねぇ。
たろぅ…
ということでベクトルの外積です。
なぜいきなりネジの話が出てきたのかというと、外積はネジが進む方向やフレミング左手の法則のように向きが重要な要素になるからです。
外積は空間上にある２つのベクトルを使って、その２つのベクトルに垂直なベクトルを計算する方法です。
せんせそれでは詳しく見ていきましょう！
外積の公式と計算方法
外積は次のように定義されます。
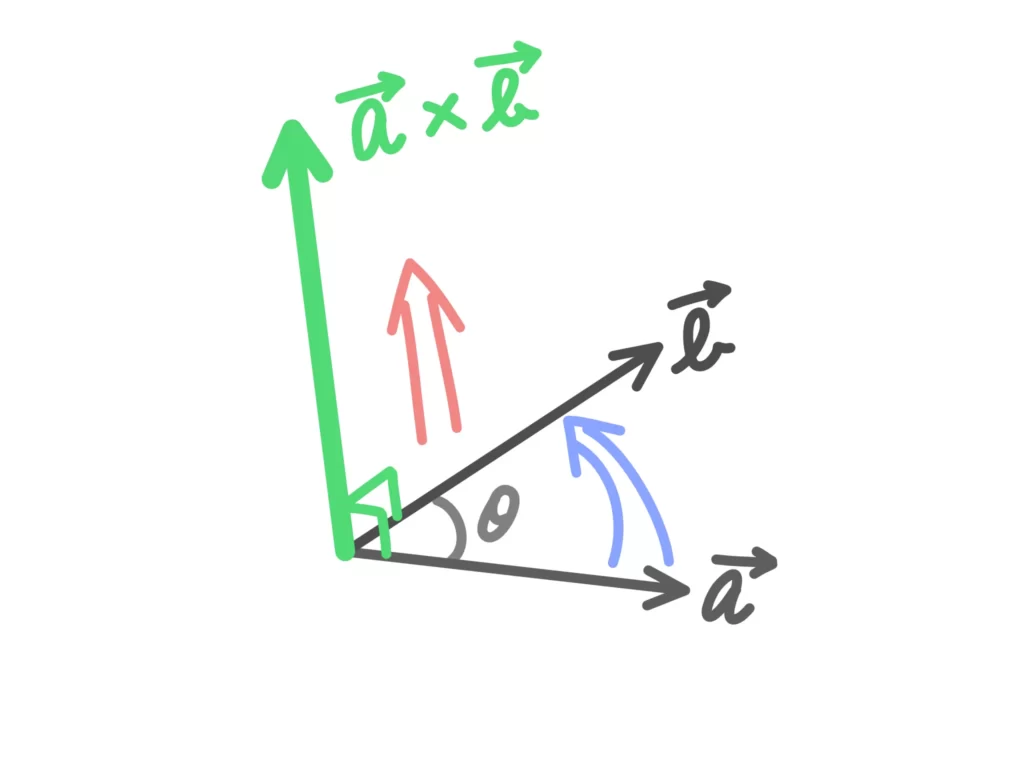
外積（図形的な定義）
\(\overrightarrow{a} \times \overrightarrow{b} = (|\overrightarrow{a}||\overrightarrow{b}|\sin{\theta})\overrightarrow{e}\)
ただし、\(\theta\)は\(\overrightarrow{a}\)と\(\overrightarrow{b}\)のなす角、
\(\overrightarrow{e}\)は\(\overrightarrow{a}\)と\(\overrightarrow{b}\)に垂直で、\(\overrightarrow{a}\)から\(\overrightarrow{b}\)へ右ネジを回転させたときに進む方向の単位ベクトル。
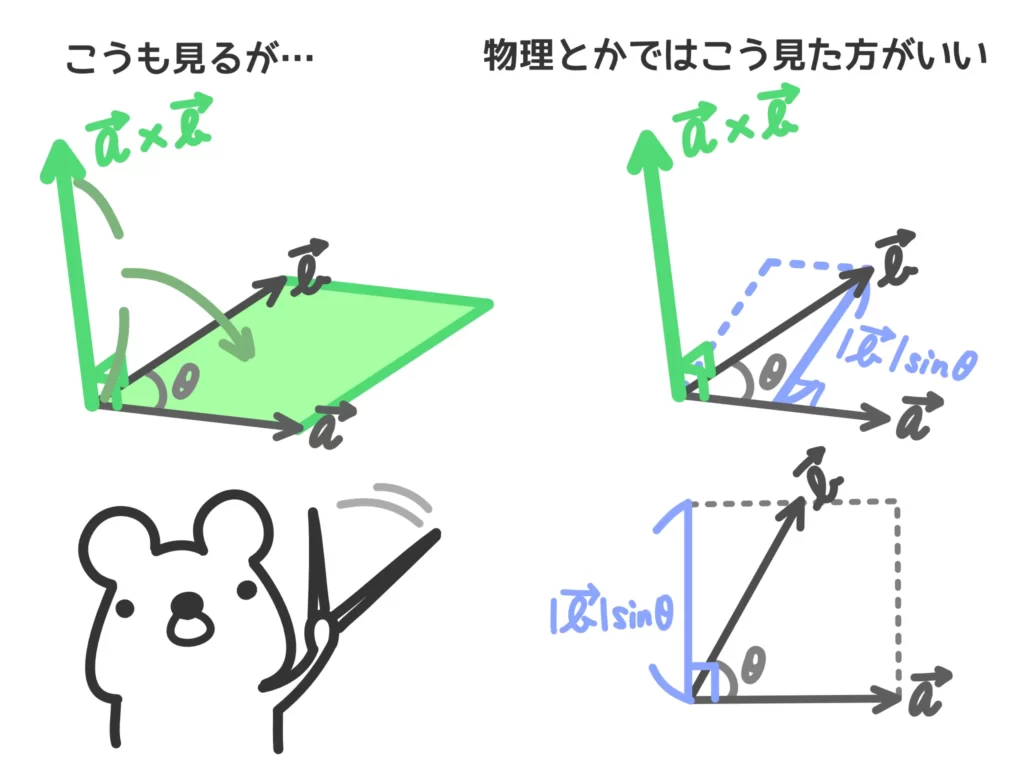
補足①「大きさについて」
「外積の大きさは\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が張る平行四辺形の面積だ」と書いている情報が多いですし、実際そうなんですが、
\(\overrightarrow{a}\)の大きさと、\(\overrightarrow{b}\)がもつ\(\overrightarrow{a}\)に垂直な成分の大きさを掛けたもの…という認識の方が重要な気がします。
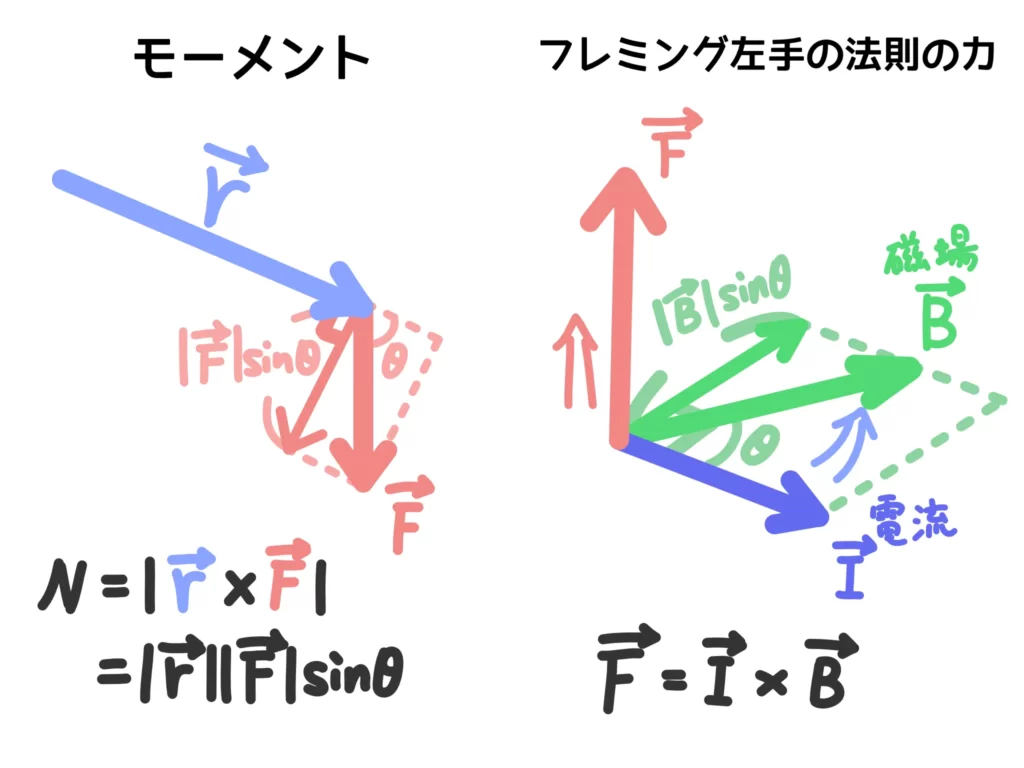
物理の計算ではモーメントやフレミング左手の法則の力を計算するときに外積を使うと、垂直成分が出て、おまけにベクトルの方向も決まるので便利です。
補足②「向きについて」
外積は
\(\overrightarrow{a} \times \overrightarrow{b}\)だったら「\(\overrightarrow{a}\)から\(\overrightarrow{b}\)へ右ネジを回転させたときに進む方向」になるので、
\(\overrightarrow{b} \times \overrightarrow{a}\)だったら「\(\overrightarrow{b}\)から\(\overrightarrow{a}\)へ右ネジを回転させたときに進む方向」になります。
つまり、
\(\overrightarrow{a} \times \overrightarrow{b}=-\overrightarrow{b} \times \overrightarrow{a}\)
となるので、交換法則が成り立たないということになります。
せんせ\(\overrightarrow{a} \rightarrow \overrightarrow{b}\)と\(\overrightarrow{b} \rightarrow \overrightarrow{a}\)は右ネジの向きで方向が逆になりますよね。
また、外積は次のように成分でも定義できます。
せんせ実践的（計算的）にはこっちの方が使えます。
外積（成分による定義）
\(\overrightarrow{a} = (a_1, a_2, a_3)\)、\(\overrightarrow{b} = (b_1, b_2, b_3)\)とすると、
\(\overrightarrow{a} \times \overrightarrow{b}=(a_2b_3-a_3b_2, a_3b_1-a_1b_3, a_1b_2-a_2b_1) \)
先ほどの外積と一致するか証明しておきましょう。
外積の定義（図形Ver）と一致するか証明
①大きさ
こちらの記事でも紹介しましたが、空間にある\(\overrightarrow{a} = (a_1, a_2, a_3)\)、\(\overrightarrow{b} = (b_1, b_2, b_3)\)が作る三角形の面積\(S\)は
\(\displaystyle S=\frac{1}{2} \sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a}\cdot\overrightarrow{b})^2}\)
で計算できます。今回、外積の大きさは\(\overrightarrow{a} = (a_1, a_2, a_3)\)、\(\overrightarrow{b} = (b_1, b_2, b_3)\)が作る平行四辺形の大きさと等しい、つまり三角形の面積\(S\)の2倍となるので
（外積の大きさ）=\(\displaystyle 2S= \sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a}\cdot\overrightarrow{b})^2}\)
となることを証明すればOKです。
せんせ舌の根も乾かないうちに「大きさは平行四辺形の面積」と言っちゃってますが、あくまで証明…ということでご了承ください。
（証明）
\(\displaystyle 2S= \sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a}\cdot\overrightarrow{b})^2}\)
\(\quad = \sqrt{(a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2)-(a_1b_1+a_2b_2+a_3b_3)^2}\)
\(\quad = \sqrt{a_1^2b_2^2+a_2^2b_1^2+a_2^2b_3^2+a_3^2b_2^2+a_3^2b_1^2+a_1^2b_3^2-2a_1b_2a_2b_1-2a_2b_3a_3b_2-2a_3b_1a_1b_3}\)
=\(\sqrt{(a_2b_3-a_3b_2)^2+ (a_3b_1-a_1b_3)^2+ (a_1b_2-a_2b_1)^2}\)=（外積の大きさ）（終）
②２つのベクトルと垂直
\(\overrightarrow{a} \times \overrightarrow{b}=(a_2b_3-a_3b_2, a_3b_1-a_1b_3, a_1b_2-a_2b_1)\)が、\(\overrightarrow{a} = (a_1, a_2, a_3)\)と\(\overrightarrow{b} = (b_1, b_2, b_3)\)の２つのベクトルと垂直、ということを示します。
せんせこれは内積を計算するだけでOKですね。
（証明）
\((\overrightarrow{a} \times \overrightarrow{b})\cdot \overrightarrow{a} = (a_2b_3-a_3b_2)a_1+( a_3b_1-a_1b_3)a_2+( a_1b_2-a_2b_1)a_3\)
\(\quad = a_1a_2b_3-a_1a_3b_2+a_2a_3b_1-a_2a_1b_3+a_3a_1b_2-a_3a_2b_1\)
\(\quad =0\)
\((\overrightarrow{a} \times \overrightarrow{b})\cdot \overrightarrow{b} = (a_2b_3-a_3b_2)b_1+( a_3b_1-a_1b_3)b_2+( a_1b_2-a_2b_1)b_3\)
\(\quad = a_2b_3b_1-a_3b_2b_1+a_3b_1b_2-a_1b_3b_2+a_1b_2b_3-a_2b_1b_3\)
\(\quad =0\)
よって、\((\overrightarrow{a} \times \overrightarrow{b})⊥\overrightarrow{a}\)かつ\((\overrightarrow{a} \times \overrightarrow{b})⊥\overrightarrow{b}\)（終）
③右ねじ向きであることの証明
（証明）
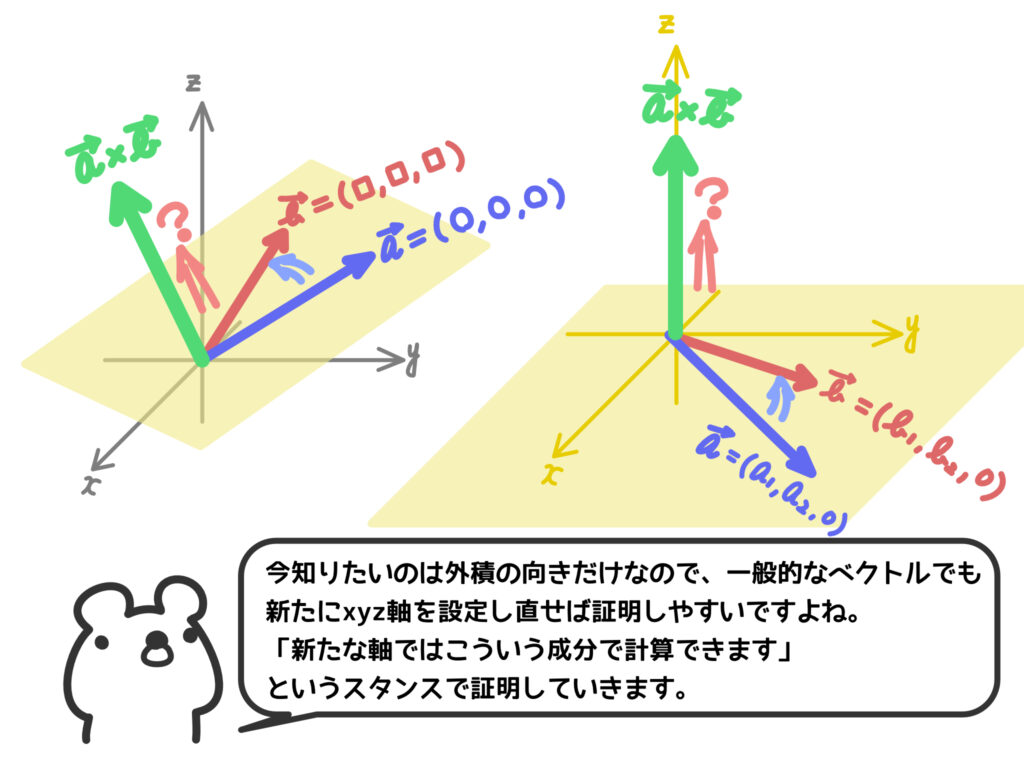
\(\overrightarrow{a} = (a_1, a_2, 0)\)、\(\overrightarrow{b} = (b_1, b_2, 0)\)とき、\(\overrightarrow{a} \times \overrightarrow{b}=(0,0, a_1b_2-a_2b_1)\)の\(z\)成分が正である、ということを示せばよいです。
ただし、\(\overrightarrow{a}\)と\(x\)軸正の方向が成す角\(\theta_1\)（\(0 \leq \theta_1 < 2\pi\)）、\(\overrightarrow{b}\)と\(x\)軸正の方向が成す角\(\theta_2\)（\(0 \leq \theta_2 < 2\pi\)）とすると、
\(0 < \theta_2-\theta_1 < \pi\)または\(0 <2\pi+ \theta_2-\theta_1 < \pi\)であるとします。
せんせちょっとわかりにくいですが、\(0 < \theta_2-\theta_1 < \pi\)または\(0 <2\pi+ \theta_2-\theta_1 < \pi\)じゃないと\(\overrightarrow{a}\)と\(\overrightarrow{b}\)の位置関係が右ねじ向きになりません。
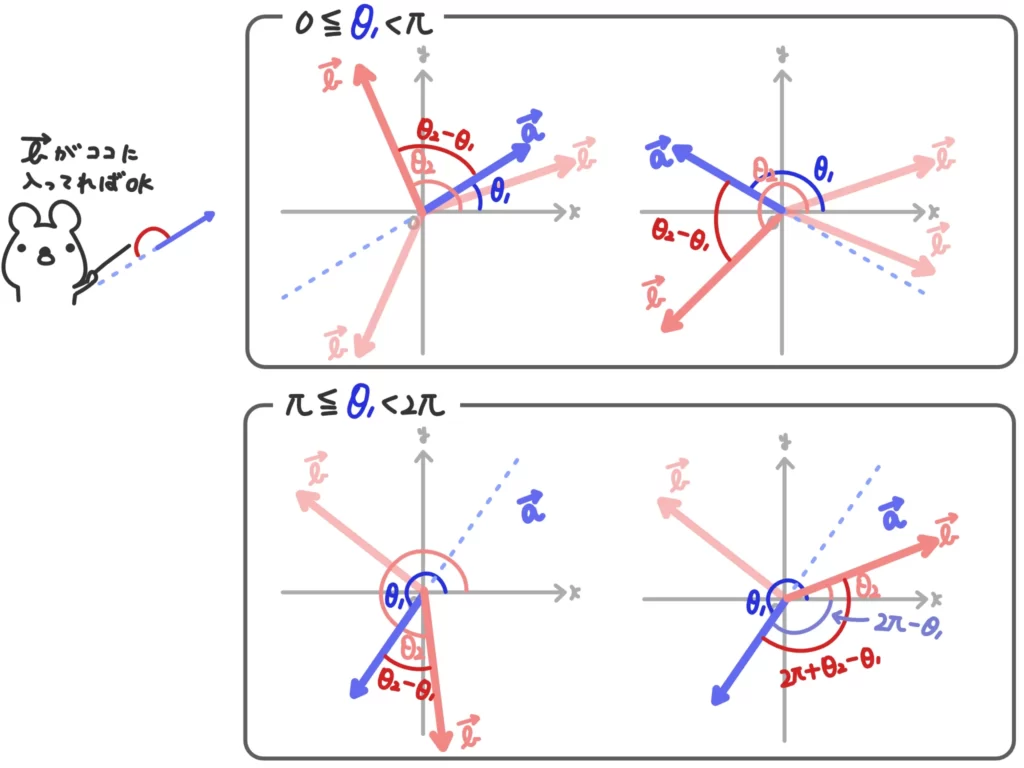
また、\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が一直線上になるときは考えません。このとき、外積は\(\overrightarrow{0}\)となるので向きをもたないからです。
\(a_1 = |\overrightarrow{a}|\cos{\theta_1},a_2 = |\overrightarrow{a}|\sin{\theta_1}\)、\(b_1 = |\overrightarrow{b}|\cos{\theta_2},b_2 = |\overrightarrow{b}|\sin{\theta_2}\)とすると、
\(a_1b_2-a_2b_1 = |\overrightarrow{a}|\cos{\theta_1}|\overrightarrow{b}|\sin{\theta_2}-|\overrightarrow{a}|\sin{\theta_1}|\overrightarrow{b}|\cos{\theta_2}\)
\(\quad = |\overrightarrow{a}||\overrightarrow{b}|(\sin{\theta_2}\cos{\theta_1}-\cos{\theta_2}\sin{\theta_1})\)
\(\quad = |\overrightarrow{a}||\overrightarrow{b}|\sin{(\theta_2-\theta_1)}\)
\(0 < \theta_2-\theta_1 < \pi\)または\(0 <2\pi+ \theta_2-\theta_1 < \pi\)より
\(0 < \theta_2-\theta_1 < \pi\)または\(-2\pi <\theta_2-\theta_1 < -\pi\)
このとき\(\sin{(\theta_2-\theta_1)}>0\)なので、
\(a_1b_2-a_2b_1 = |\overrightarrow{a}||\overrightarrow{b}|\sin{(\theta_2-\theta_1)}>0\)
よって、外積の向きは右ねじ進行方向となります。（終）
外積って使えるのは3次元だけ？2次元では使えないの？
結論、外積は３次元（空間）でしか使えません。
２次元で同じように、\(\overrightarrow{a} = (a_1, a_2)\)、\(\overrightarrow{b} = (b_1, b_2)\)について計算しようとしたら、
\(a_1b_2-a_2b_1\)
のようになるかもしれませんが、これは２つのベクトル\(\overrightarrow{a} = (a_1, a_2)\)、\(\overrightarrow{b} = (b_1, b_2)\)が張る平行四辺形の符号付き面積…くらいの意味しかありません。
もちろんこれを外積とも呼びません。
せんせそういう意味では「外積の大きさ」くらいの意味はもたせることができますが、あんまり意味のある計算ではない気がします…
。
外積の具体的な使い道
せんせ特に座標空間では成分計算を使ってガリガリ計算するのに役立ちます！
平面の方程式を求める
平面の方程式は次のように計算することができます。
平面の方程式
\(\overrightarrow{n}=(a,b,c)\)に垂直で点\((x_0,y_0,z_0)\)を通る平面の方程式は
\(a(x-x_0)+b(y-y_0)+c(z-z_0)=0\)
平面の方程式を求める際には平面に垂直な法線ベクトル\(\overrightarrow{n}\)を使うのが一番手っ取り早いです。
が、いつも法線ベクトルが与えられるわけではありません。
例．3点A\((1,1,0)\)、B\((3,1,2)\)、C\((3,3,0)\)を通る平面の方程式を求めよ。
外積を使わないで解こうとすると、法線ベクトルを\(\overrightarrow{n}=(a,b,c)\)として置くか、点P\((x,y,z)\)が平面ABC上にあるときに\(\overrightarrow{OP} =s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\)と置けることを利用するしかありません。
どのみち、置く文字が膨れ上がるので面倒です。
せんせ外積を使えば、直接法線ベクトルを一つ求めることができるので、外積で得られたベクトルと上記の公式で一発です。
（解答）
\(\overrightarrow{AB} = (2,0,2)=2(1,0,1)\)、\(\overrightarrow{AC} = (2,2,0)=2(1,1,0)\)より、
\(\overrightarrow{a} = (1,0,1)\)と
\(\overrightarrow{b} = (1,1,0)\)とすると、（←素直に\(\overrightarrow{AB}\)、\(\overrightarrow{AC}\)を使う必要はない。）
\(\overrightarrow{a} \times \overrightarrow{b} = (-1, 1, 1)\)
よって、求める平面の方程式は
\( (-1)\cdot(x-1)+1\cdot(y-1)+1\cdot z=0\)
\( x-y-z=0\)…（答）
空間にある三角形の面積を求める
こちらの記事で空間にある三角形の面積を求めるには、
「\(\displaystyle S = \frac{1}{2}\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a}\cdot \overrightarrow{b})^2}\)を使うしかない」
と言いましたが、ちょっとウソです。
高校の範囲外ではありますが、外積を使えば一発で計算できます。
空間にある三角形の面積
空間にあるベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)が作る三角形ABCの面積\(S\)は
\(\displaystyle S = \frac{1}{2}|\overrightarrow{AB} \times \overrightarrow{AC}|\)
超シンプルです！
「外積の大きさは\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が張る平行四辺形の面積」だからです。半分にすれば三角形の面積になります。
せんせ…「やっぱり外積の大きさは２つのベクトルが張る平行四辺形の面積じゃねぇか！」というツッコミは受け付けません。
例．3点A\((1,1,0)\)、B\((3,1,2)\)、C\((3,3,0)\)としたとき、三角形ABCの面積\(S\)を求めよ。
（解答）
\(\overrightarrow{AB} = (2,0,2)=2(1,0,1)\)、\(\overrightarrow{AC} = (2,2,0)=2(1,1,0)\)より、
\(\overrightarrow{AB} \times \overrightarrow{AC} = 4(-1, 1, 1)\)（←外積には\((k\overrightarrow{a})\times \overrightarrow{b} = k(\overrightarrow{a} \times \overrightarrow{b})\)という性質がある）
よって\(\displaystyle S=\frac{1}{2}|\overrightarrow{AB} \times \overrightarrow{AC}| = \frac{1}{2}4\sqrt{(-1)^2+1^2+1^2}=2\sqrt{3}\)…（答）
（ちなみに…別解）
せんせ\(\displaystyle S = \frac{1}{2}\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a}\cdot \overrightarrow{b})^2}\)を使うとこんな感じです。
\(\overrightarrow{AB} = (2,0,2)=2(1,0,1)\)、\(\overrightarrow{AC} = (2,2,0)=2(1,1,0)\)より、
\(\overrightarrow{AB} \cdot \overrightarrow{AC} = 4(1\cdot 1 + 0 \cdot 1+ 1 \cdot 0) = 4\)
よって\(\displaystyle S = \frac{1}{2}\sqrt{|2\sqrt{2}|^2|2\sqrt{2}|^2-(4)^2} =\frac{1}{2}4 \sqrt{2\cdot 2 – 1} = 2\sqrt{3} \)…（答）
四面体の体積を求める
これは結構強力です。
四面体の体積
\(\overrightarrow{AB}\)、\(\overrightarrow{AC}\)、\(\overrightarrow{AD}\)で作られる四面体ABCDの体積\(V\)は
\(\displaystyle V=\frac{1}{6}|(\overrightarrow{AB} \times \overrightarrow{AC}) \cdot \overrightarrow{AD}| \)
（説明）
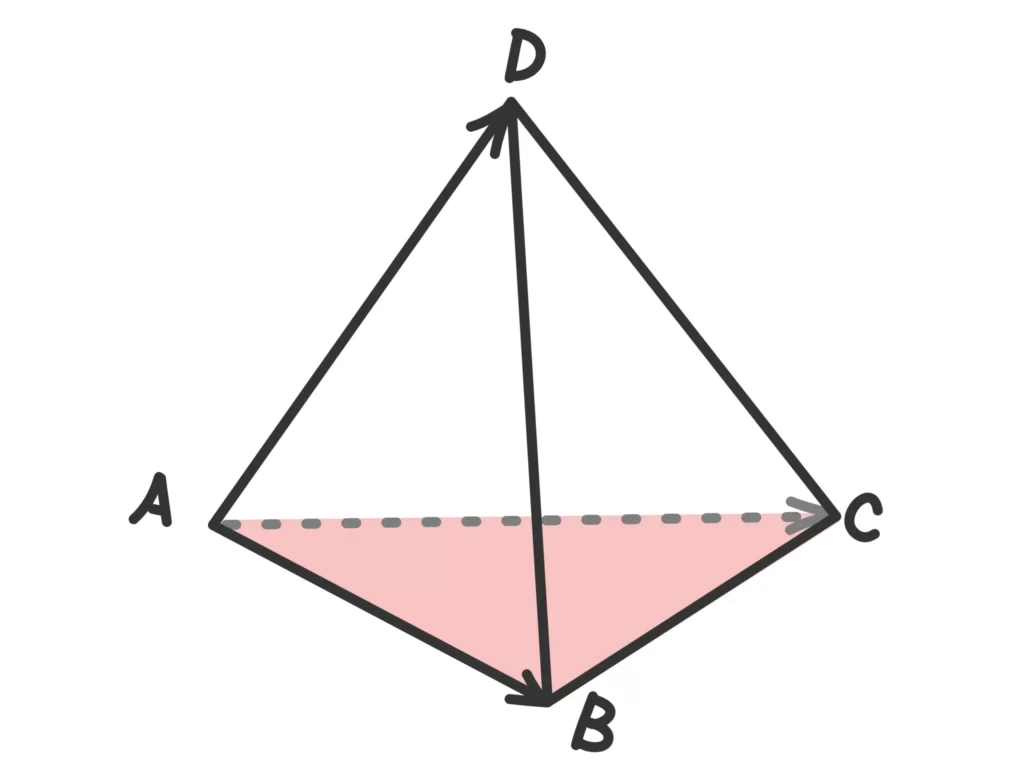
上の図のように底面を三角形ABCとすると、\(\displaystyle \frac{1}{2}(\overrightarrow{AB} \times \overrightarrow{AC})\)は、
\(\displaystyle \frac{1}{2}(\overrightarrow{AB} \times \overrightarrow{AC}) = \Big( \frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|\sin{\theta} \Big) \overrightarrow{e}\)
となります。（\(\theta\)は\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の成す角、\(\overrightarrow{e}\)は\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)に垂直で\(\overrightarrow{AB}\)→\(\overrightarrow{AC}\)の右ネジの進む方向の単位ベクトル。）
ここで、\(\displaystyle \frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|\sin{\theta}\)は三角形ABCの面積、\(\overrightarrow{e}\)は三角形ABCに垂直な単位ベクトル、というのを確認してください。
これと、さらに\( \overrightarrow{AD} \)との内積を取ります。
\(\displaystyle \frac{1}{2}(\overrightarrow{AB} \times \overrightarrow{AC}) \cdot \overrightarrow{AD} = \frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|\sin{\theta}(\overrightarrow{e} \cdot \overrightarrow{AD}) \)
すると、\( (\overrightarrow{e} \cdot \overrightarrow{AD}) = |\overrightarrow{AD}|\cos{\phi} \)（ただし、\(\phi\)は\(\overrightarrow{e}\)と \(\overrightarrow{AD}\)の成す角）となり、\( (\overrightarrow{e} \cdot \overrightarrow{AD})\)は四面体D-ABCの符号付きの高さになります。
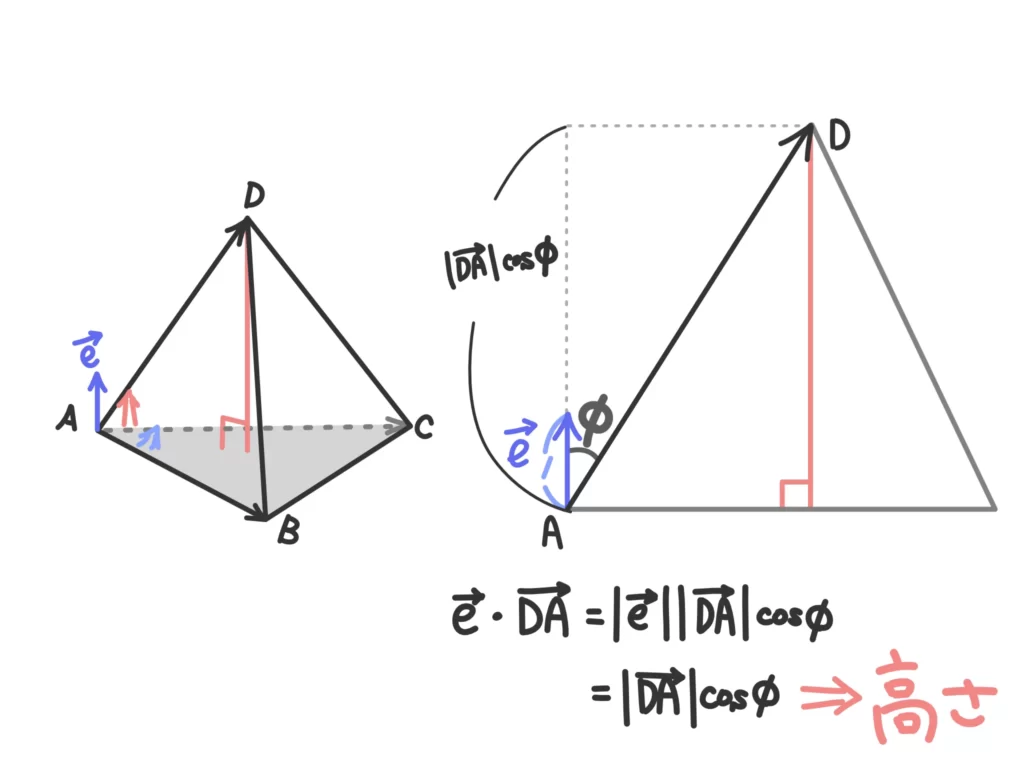
よって、\(\displaystyle |\frac{1}{2}(\overrightarrow{AB} \times \overrightarrow{AC}) \cdot \overrightarrow{AD}|\)は（底面積）×（高さ）を表すので、これに\(\displaystyle \frac{1}{3}\)を掛けた、
\(\displaystyle \frac{1}{6}|(\overrightarrow{AB} \times \overrightarrow{AC}) \cdot \overrightarrow{AD}| \)は四面体ABCDの体積を表します。
例．4点A\((1,1,0)\)、B\((3,1,2)\)、C\((3,3,0)\)、D\((2,1,4)\)としたとき、四面体ABCDの面積\(V\)を求めよ。
（解答）
\(\overrightarrow{AB} = (2,0,2)=2(1,0,1)\)、\(\overrightarrow{AC} = (2,2,0)=2(1,1,0)\)より、
\(\overrightarrow{AB} \times \overrightarrow{AC} = 4(-1, 1, 1)\)
また、\(\overrightarrow{AD} = (1,0,4)\)なので、
\((\overrightarrow{AB} \times \overrightarrow{AC})\cdot \overrightarrow{AD} = 4 \{ (-1)\cdot 1 +1 \cdot 0 + 1 \cdot 4 \} = 12\)
よって、\(\displaystyle V = \frac{1}{6}|12| = 2\) …（答）
ちなみに別解
せんせ高校で教わる知識内で解こうとしたら、普通はこんな感じです。
三角形ABCの面積\(S\)とする。
\(\overrightarrow{AB} = (2,0,2)=2(1,0,1)\)、\(\overrightarrow{AC} = (2,2,0)=2(1,1,0)\)より、
\(\overrightarrow{AB} \cdot \overrightarrow{AC} = 4(1\cdot 1 + 0 \cdot 1+ 1 \cdot 0) = 4\)
よって\(\displaystyle S = \frac{1}{2}\sqrt{|2\sqrt{2}|^2|2\sqrt{2}|^2-(4)^2} =\frac{1}{2}4 \sqrt{2\cdot 2 – 1} = 2\sqrt{3} \)
点Dから平面ABCに垂線DHを下ろすと、
\(\overrightarrow{DH} = \overrightarrow{DA} + s\overrightarrow{AB}+t\overrightarrow{AC}\)とおける。成分計算をすると、
\(\overrightarrow{DH} = (2s+2t-1, 2t, 2s-4)\)
\(\overrightarrow{DH}\)⊥\(\overrightarrow{AB}\)より、\(\overrightarrow{DH} \cdot \overrightarrow{AB}=0\)
\((2s+2t-1, 2t, 2s-4)\cdot 2(1,0,1) =0\)
\(4s+2t-5 = 0\)…①
\(\overrightarrow{DH}\)⊥\(\overrightarrow{AC}\)より、\(\overrightarrow{DH} \cdot \overrightarrow{AC}=0\)
\((2s+2t-1, 2t, 2s-4)\cdot 2(1,1,0) =0\)
\(2s+4t-1 = 0\)…②
①、②より\(\displaystyle s=\frac{3}{2}\)、\(\displaystyle t=-\frac{1}{2}\)
よって、\(\overrightarrow{DH} = (1, -1, -1)\)なので、\(|\overrightarrow{DH}| = \sqrt{3}\)
以上より、求める体積\(V\)は
\(\displaystyle V = \frac{1}{3} \cdot 2\sqrt{3} \cdot \sqrt{3} = 2\)…（答）
たろぅ…。
まとめ
高校数学の範囲外ですが、外積のお話でした。
高校範囲外とはいえ、成分による外積の計算方法を知っていると計算が楽になる部分もあります。
外積の意味も知っていればかなり役に立つので、座標空間のベクトル計算も極めていきたい！という人は学んでおいてソンはないところですね。
ちょっと一息
このブログで活躍してるクマのLINEスタンプもあります！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
