ベクトルを使った三角形の面積公式【証明から覚え方のコツまで】

2023年12月22日

ベクトルを使った三角形の面積公式。

あれ、ちょっと覚えにくいんですよね…。また、平面では別の公式もあったりして結構厄介です。

この記事では三角形の面積公式の証明と覚え方について説明していきます。

ベクトルを使った三角形の面積公式

たろぅ

…間違えた。なぜ…なぜなんだ…
。

はなこ

あら、たろうくん、顔色が２２世紀から来た猫型ロボットみたいな色になってるわよ？

たろぅ

別にネズミに耳をかじられたわけじゃねぇし…。さっき返された期末テストの、ベクトルで三角形の面積を求める問題…公式うろ覚えだったから、間違えてしまった…。

はなこ

あっそう。でもこれ、公式使うだけでしょ？ツメが甘いわね。

たろぅ

なんでこの問題が１０点分もあるんだぁ！

はなこ

（せんせいの優しさがアダとなったわね…）

ということで、ベクトルを使って三角形の面積を求めるお話です。

早速ですが、ベクトルを使った三角形の面積公式の確認をしていきましょう。

せんせ

サクッと確認→証明→覚え方とか注意点、といきましょう！

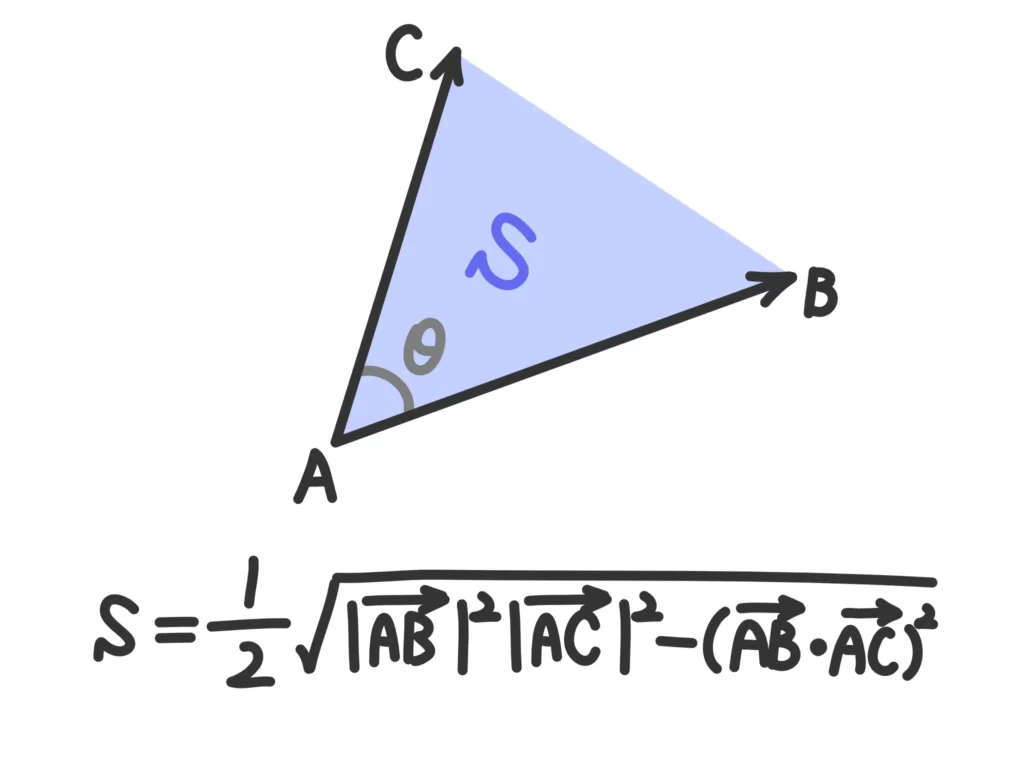
ベクトルを使った三角形の面積公式

\(\overrightarrow{AB}\)、\(\overrightarrow{AC}\)が作る三角形ABCの面積\(S\)は

\(\displaystyle S = \frac{1}{2}\sqrt{|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2-(\overrightarrow{AB}\cdot \overrightarrow{AC})^2}\)

三角形の面積公式の証明

この公式、複雑…というか、なんとなく覚えにくいですよね。

ですが、公式の証明の方針を覚えていれば公式自体も覚えやすいかな、と思います。

せんせ

\(|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2\)の２乗を落とすとか、\(|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2\)と\((\overrightarrow{AB}\cdot \overrightarrow{AC})^2\)の位置を逆にしちゃうとか、そんなところで間違えることが多いです。

（証明）

\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の成す角を\(\theta\)とする。ただし、\(0° < \theta <180°\)とする。

\( \displaystyle \frac{1}{2}\sqrt{|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2-(\overrightarrow{AB}\cdot \overrightarrow{AC})^2} = \frac{1}{2}\sqrt{|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2-|\overrightarrow{AB}|^2| \overrightarrow{AC}|^2\cos^2{\theta}}\)
\(\displaystyle \quad = \frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|\sqrt{1-\cos^2{\theta}}\)
\(\displaystyle \quad = \frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|\sqrt{\sin^2{\theta}}\)
\(\displaystyle \quad = \frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|\sin{\theta}\)（∵\(0° < \theta <180°\)より\(\sin{\theta}>0\)）

これは三角形ABCの面積\(S\)である。（終）

ポイントは、

① 最終的に\(\displaystyle S = \frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|\sin{\theta}\)の形に持っていっている。

② だから\(\sqrt{　}\)の中身である「ベクトルの大きさ」は\(\sqrt{　}\)の外に出すために２乗しておかなければならない。

③ \(\sin{\theta}\)を導き出すために、\(\sin^2{\theta} = 1-\cos^2{\theta}\)を使っている。そのために内積の式\(\overrightarrow{AB} \cdot \overrightarrow{AC}=|\overrightarrow{AB}|| \overrightarrow{AC}|\cos{\theta}\)の\(\cos{\theta}\)を利用しているので、当然、内積も２乗するし、内積のほうが後ろにくる。

というところですね。

せんせ

・三角形の面積\(\displaystyle S = \frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|\sin{\theta}\)
・\(\sin^2{\theta} = 1-\cos^2{\theta}\)
・内積\( |\overrightarrow{AB}|| \overrightarrow{AC}|\cos{\theta}\)
の式の形を意識すれば覚えやすいですね。

2次元で3点が与えられてるときには？

２次元（平面）では、ベクトルの成分を使って三角形の面積を求めることができます。

成分を使った三角形の面積公式

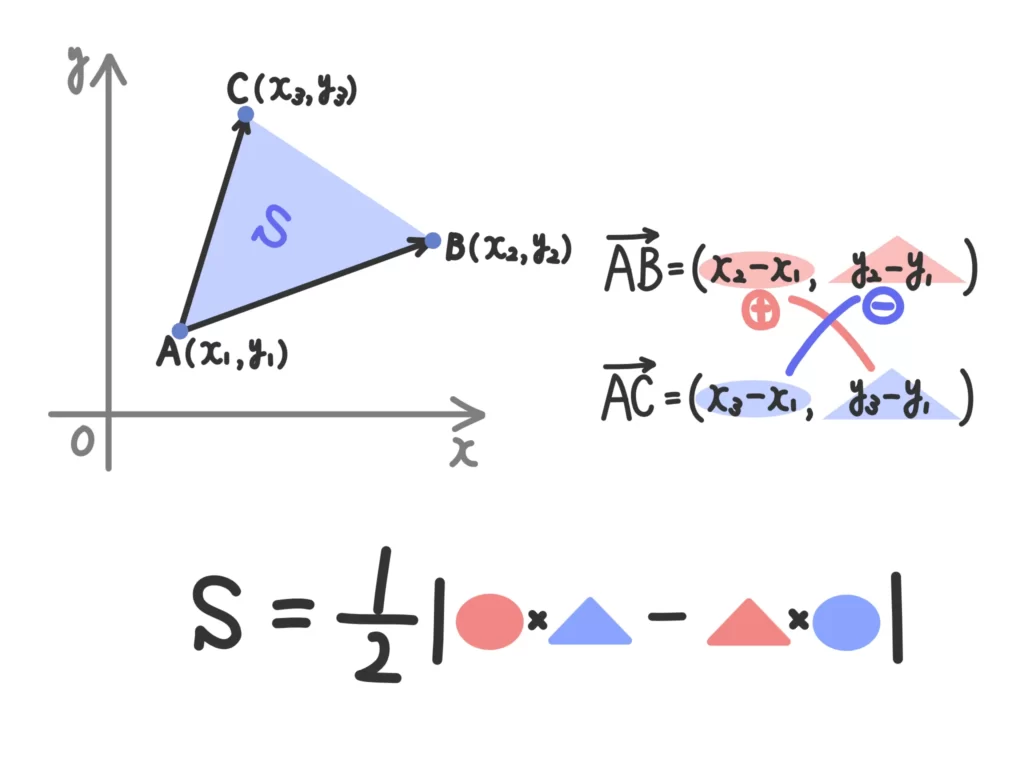
\(\overrightarrow{AB} = (a_1, a_2)\)、\(\overrightarrow{AC} = (b_1, b_2)\)とすると、三角形ABCの面積\(S\)は

\(\displaystyle S=\frac{1}{2} |a_1b_2 -a_2b_1| \)

せんせ

証明は、成分表示で上で紹介した面積公式をガリガリ計算するだけです。

（証明）

\(\overrightarrow{AB} = (a_1, a_2)\)、\(\overrightarrow{AC} = (b_1, b_2)\)より、

\(|\overrightarrow{AB}|^2 = a_1^2+ a_2^2 \)、
\(|\overrightarrow{AC}|^2 = b_1^2+ b_2^2\)、
\((\overrightarrow{AB}\cdot \overrightarrow{AC})^2=(a_1b_1+a_2b_2)^2\)。

よって、

\(\displaystyle S = \frac{1}{2}\sqrt{|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2-(\overrightarrow{AB}\cdot \overrightarrow{AC})^2}\)
\(\displaystyle \quad = \frac{1}{2}\sqrt{(a_1^2+ a_2^2)(b_1^2+ b_2^2)-(a_1b_1+a_2b_2)^2}\)
\(\displaystyle \quad = \frac{1}{2}\sqrt{a_1^2b_2^2+ a_2^2b_1^2-2a_1b_1a_2b_2}\)
\(\displaystyle \quad = \frac{1}{2}\sqrt{(a_1b_2 -a_2b_1)^2}\)
\(\displaystyle \quad = \frac{1}{2}|a_1b_2 -a_2b_1|\)（終）

ということで、座標平面上の３点A\((x_1,y_1)\)、B\((x_2,y_2)\)、C\((x_3,y_3)\)が与えられているときには、

一度\(\overrightarrow{AB} = (x_2-x_1, y_2-y_1)\)、\(\overrightarrow{AC} = (x_3-x_1, y_3-y_1)\)として、成分を計算してから上記の公式を使ってください。