PR
円順列とは？【考え方や例題を図を使いながらわかりやすく説明】
円順列は順列の計算方法の一つです。
ただ、円順列には「回して同じ並べ方になるものは同じとみなす」という厄介な性質があります。
この記事では円順列の考え方と例題を、図を使いながらわかりやすく説明していきます。
デカ丸コツを掴めば意外と簡単！
順列の考え方も使うので「順列ってなんだっけ？」という人はコチラの記事もあわせて御覧ください！
あわせて読みたい
順列(P)と階乗(!)【公式・どのような場面で使うかなど徹底解説！】
数学Aで習う順列。 順列（P）って、計算方法はわかるけどなんとなく使い所がわかりにくい…。 と思う人も多いトコロです。 この記事では順列（\(_{n}P_{r}\)）の計算方法…
目次
円順列とは
たろぅ…テンション下がるぜ
はなこあら？朝からテンション低いわね
たろぅ昨日中華料理屋に行ったんだけどさ…回転テーブルあるじゃない？上流の方でほとんど食べられてさ…あんまり食べれなかったんだよね
はなこなるほど、ざまぁ…ざんねんだったわね
たろぅもっと北京ダック食べたかったぜ…ピータンしか回ってこなかったわ
はなこ（北京ダックと…ピータン？）
ということで、円順列です。
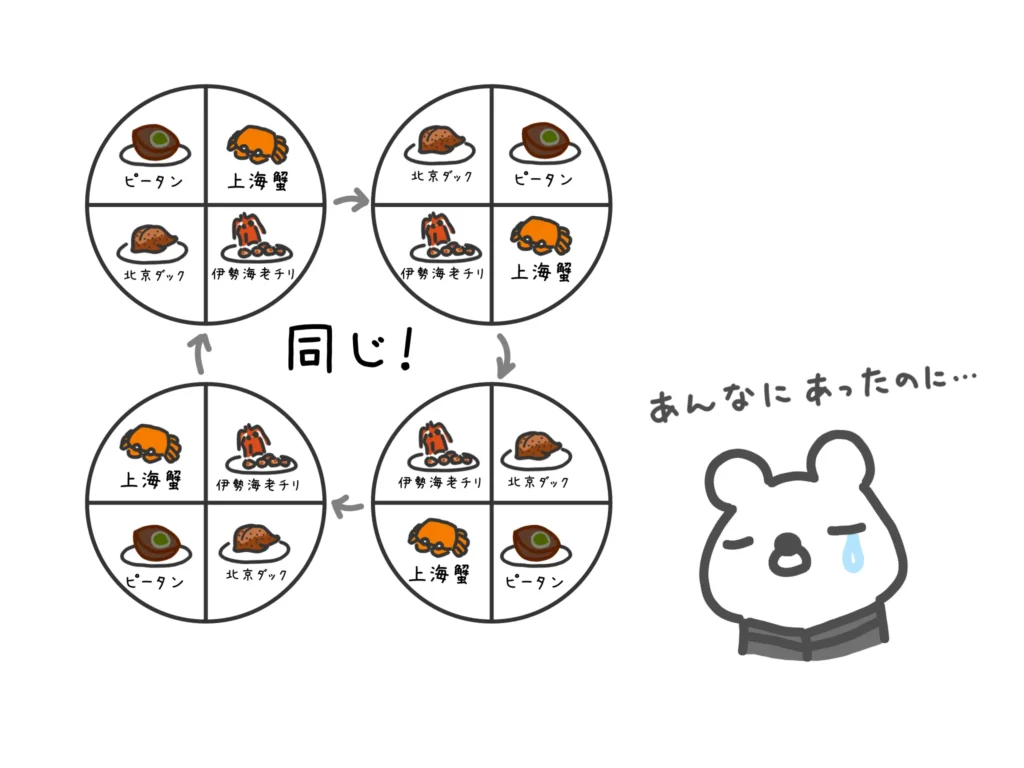
あの回転テーブル、ぐるぐる回っても、置いてある料理の並び順が変わるわけではありませんよね？
数学の円順列も基本的にこの考え方をしていきます。
つまり「回して同じ並びとなるものは同じものとみなそう」ということです。
円順列の計算方法
せんせ考え方を説明する前に、先に円順列の計算方法を載せておきます
\(n\)個のモノを円状に並べる並べ方（回して同じ並びとなるものは同じとみなす）は
\((n-1)!\)通り
たろぅえ…なんかメチャクチャ簡単じゃないですか。\(n\)個から１つ減らして階乗の計算すればいいんでしょ？意味はよくわかりませんけど…
せんせ考え方まで理解しておくと、応用問題のときも立式しやすいので、考え方も押さえておきましょう。
考え方．「円順列はひとつ固定する」
円順列を考えるときに一番問題になるのは「回る」ことです。
それなら「固定しちゃえばいいじゃない」というのが一番わかりやすい考え方です。
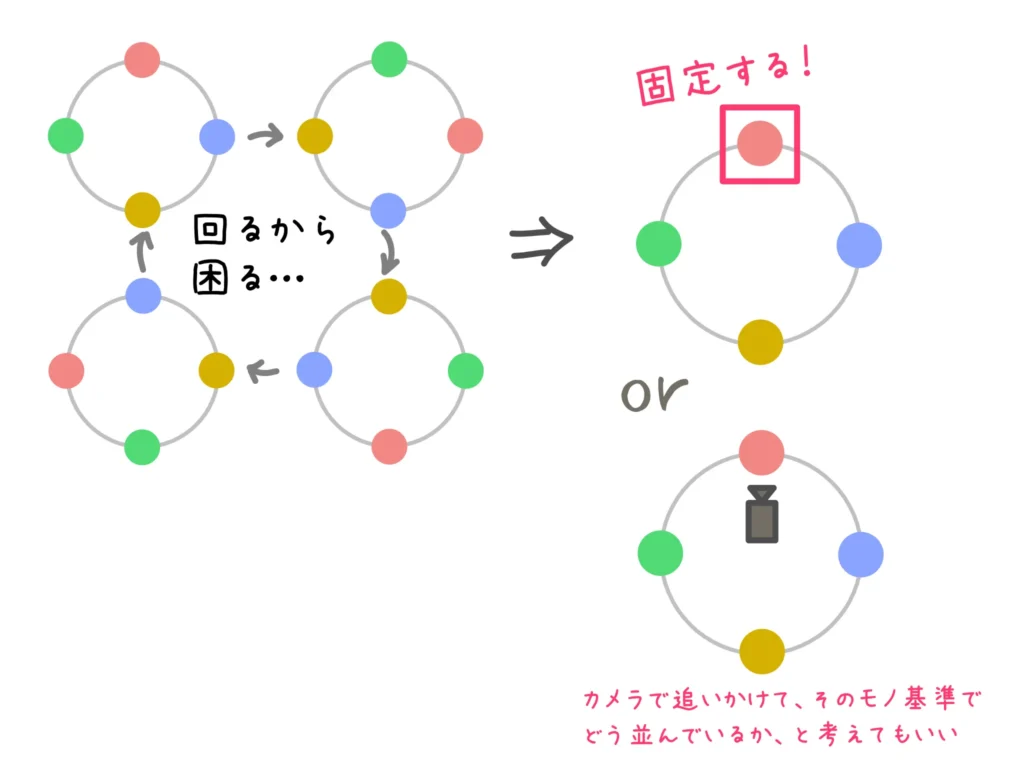
固定した上で、他のモノを順列として計算します。
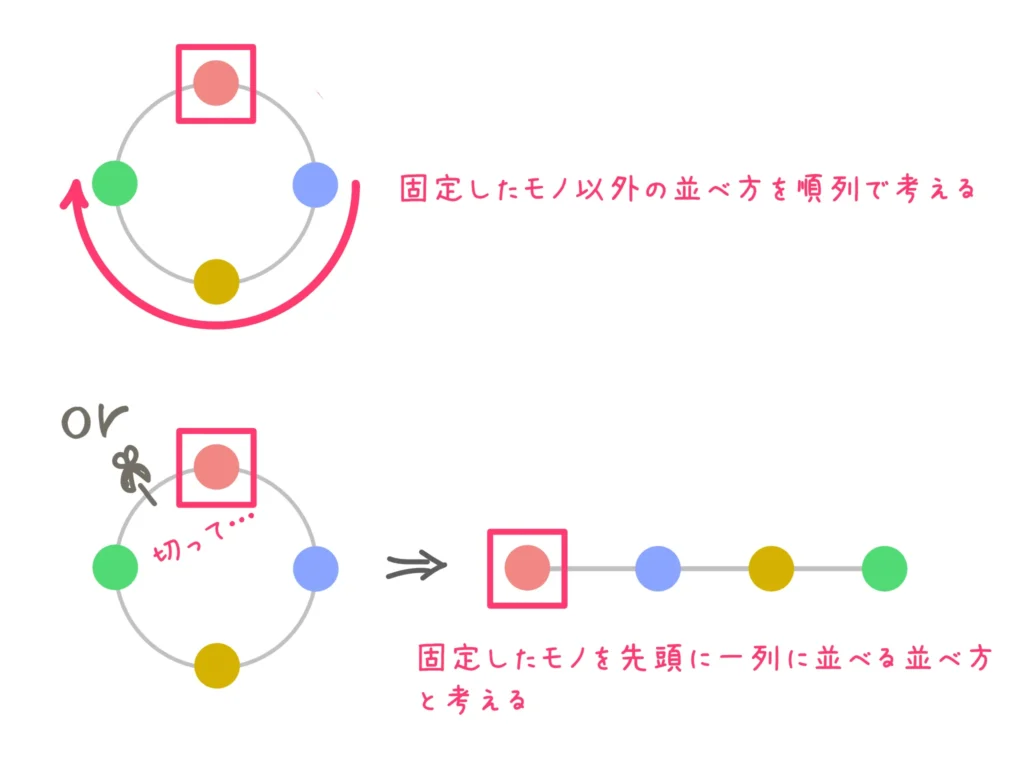
せんせ個人的には固定した横を切って１列に並べ直すイメージが好きです。
おまけ．同じとみなせる円順列を一つにまとめる
同じとみなせる円順列を一つにまとめる、という考え方もできます。
\(n\)個のモノを円形に並べるときに、何も考えずに並べる並べ方は\(n!\)通りです。
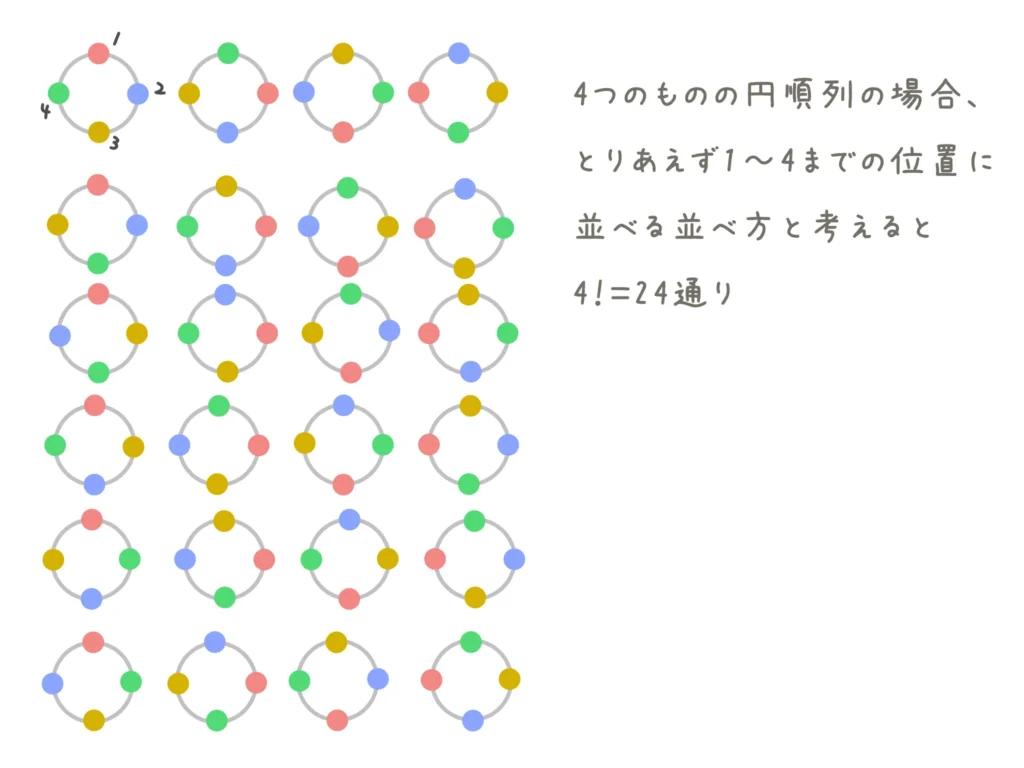
その中で、回して同じとみなせる並べ方はそれぞれ\(n\)パターンあります。
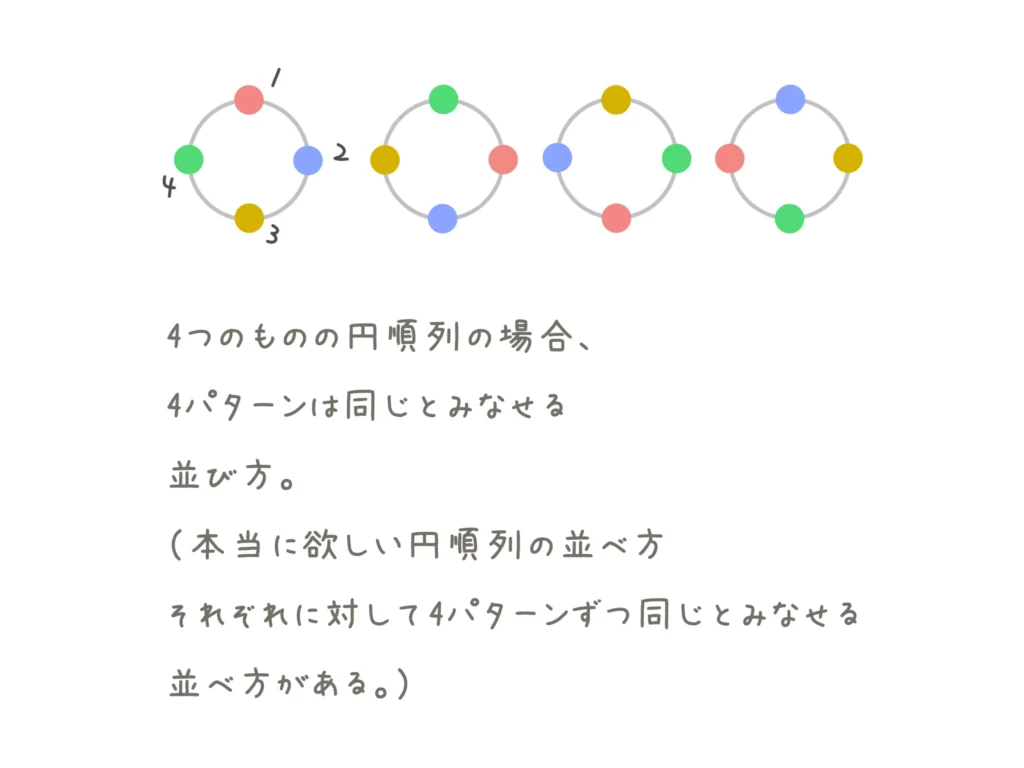
せんせ\(n\)個のモノを並べて回転させたら、\(n\)回、回転させられますよね。
それぞれ\(n\)パターン、同じとみなせる並べ方があるはずで、それらを全て合わせて数えたら\(n!\)通りあるはずです。
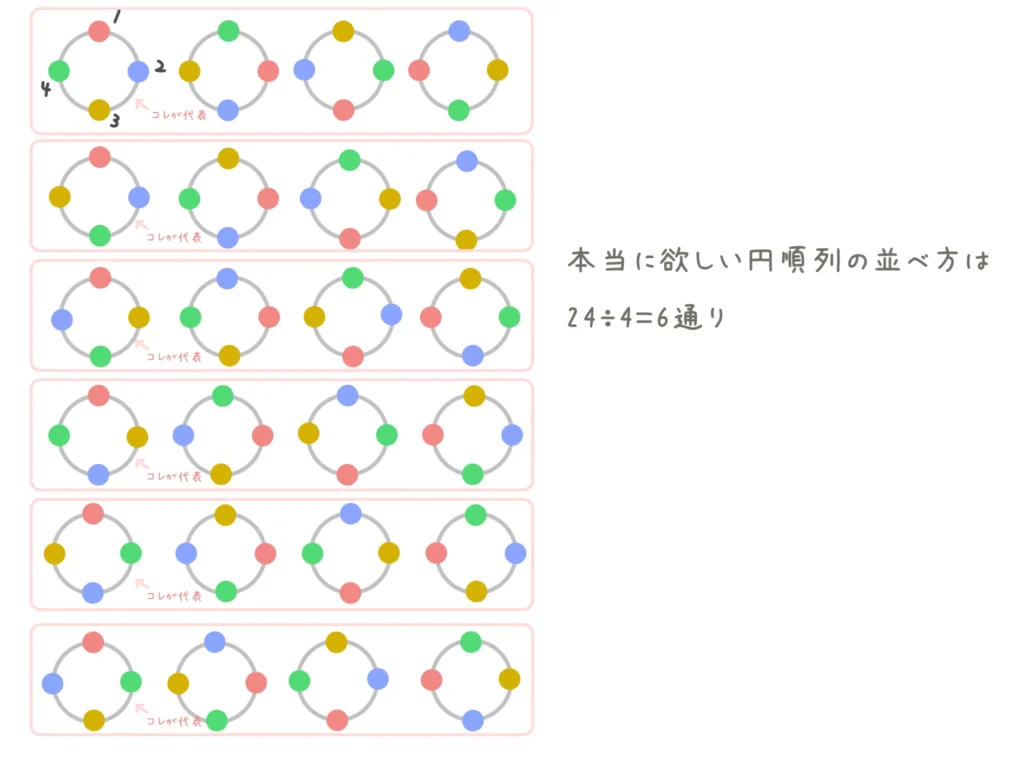
ということで、逆に「それぞれの\(n\)パターン→１パターン」にまとめればいいので、計算としては\(n!\)通りを\(n\)で割ればよいことになります。
\(\displaystyle \frac{n!}{n} = \frac{n \cdot (n-1)!}{n}=(n-1)! \)
この考え方も\(C\)や同じものを含む順列の計算をするときなどに重要なのですが、とりあえず円順列を解きたければ「固定」の考え方がわかりやすいのでそっちをオススメします。
あわせて読みたい
組み合わせ等を階乗でなぜ割るのか？具体例で説明
場合の数をやっていて疑問に思うものの一つに「組み合わせや同じものを含む順列を階乗でなぜ割るのか？」があります。 よくわからないまま覚えてしまっている人も多いと…
円順列の例題
せんせいくつか例題を出しておきましょう！
例１．\(8\)人が円卓に座る座り方は何通りあるか？ただし、回転して同じ座り方となる座り方は同じものとする。
解答はコチラ！
上記の考え方にしたがって計算すればOKです！
８人のうち、誰か１人を固定（焦点当て）します。
すると、他の７人を並べ方を考えればいいので、\(7! = 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 5040\)（通り）…（答）
例２．子ども２人、お父さん、お母さん、おじいちゃん、おばあちゃんの６人でレストランに行った。次のように円卓に座る座り方は何通りあるか？ただし、回転して同じ座り方となる座り方は同じものとする。
(1) 子ども２人が隣り合うように座る座り方。
(2) お父さん、お母さんが向かい合うように座る座り方。
解答はコチラ！
コチラの記事でも説明しましたが、場合の数・確率は条件のあるものから考えていきます。
せんせ数学に限らず、世の中の問題は条件のあるものから考えるのが鉄則です！
特に円順列の場合は、そもそも「１つ固定する」ことでその１つを特別扱いしているので、条件のあるモノを固定に使ったらスムーズに立式できます。
(1) 条件のある人は「子ども２人」なので、この子ども２人をまとめて１組として固定しちゃいます。
すると、並び方は他の４人を考えればよいので\(4!\)通り。
ただし、それぞれの並び方で子ども２人の並び方も考えないといけないので、\(2!\)通りを掛けないといけません。
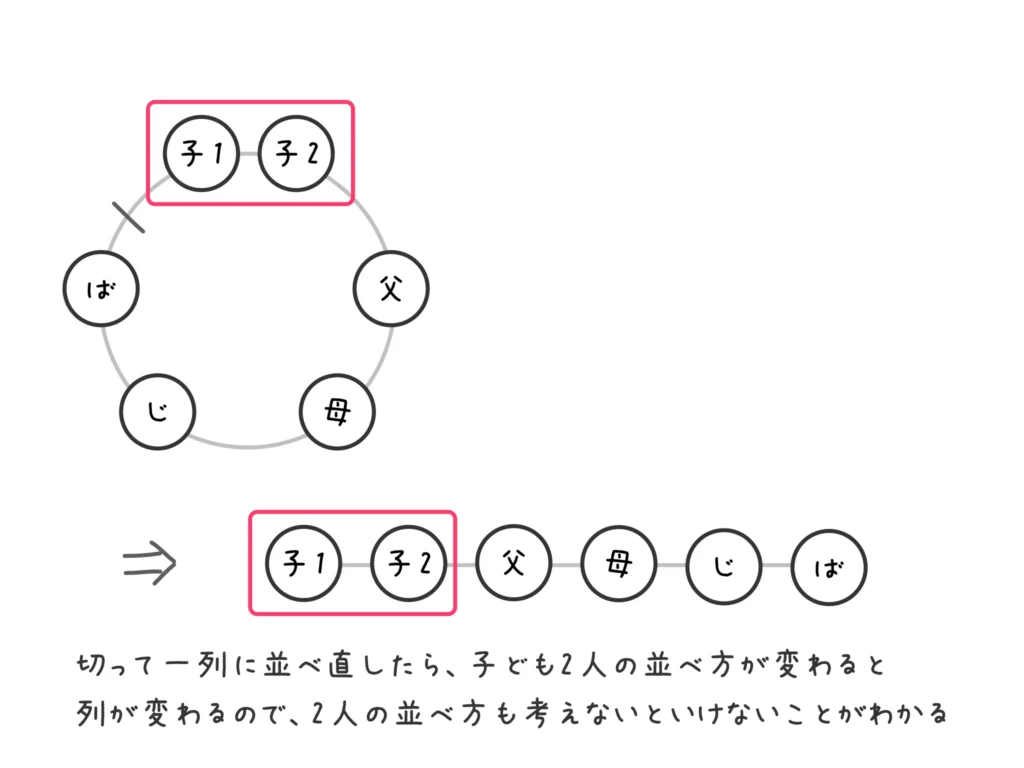
よって、\(4! \times 2! = 24 \times 2 = 48\)（通り） …（答）
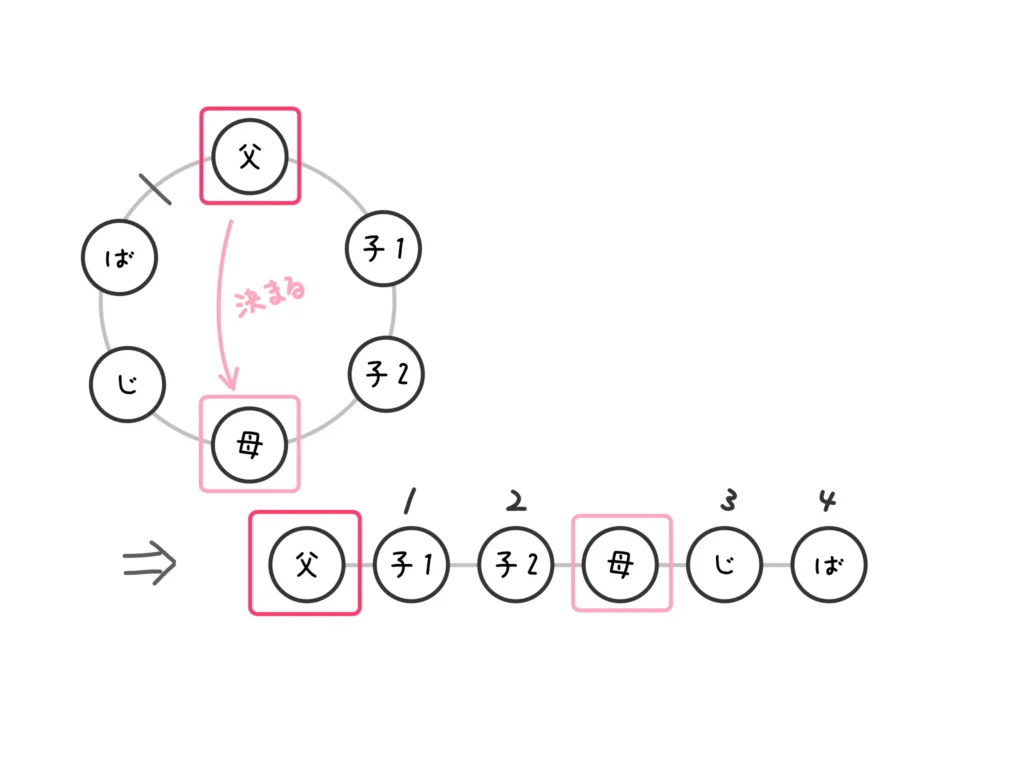
(2) 条件のある人は「お父さんとお母さん」なので、どちらかを固定します。どちらでもいいのですが、今回はお父さんにしましょう。
すると、まずお母さんの座る位置が決まります。つまり、ここまでは１通り、ということになります。
そのあとで他の４人を並べればよいので、結局\(4! = 24\)通りとなります。…（答）
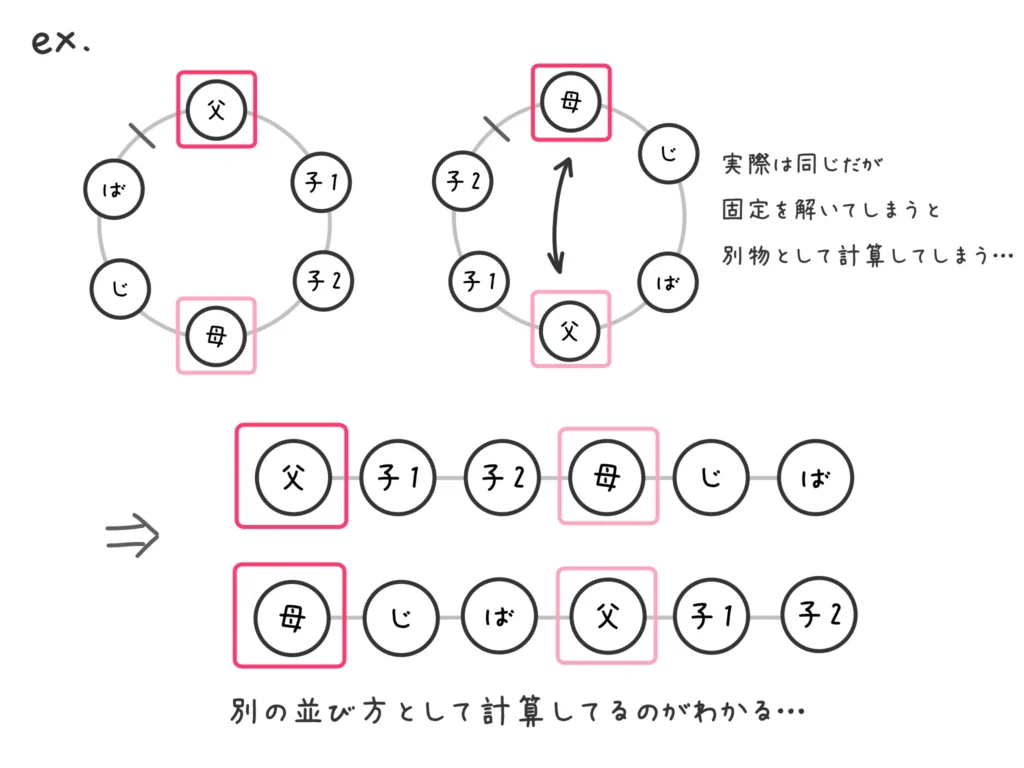
【補足】 ちなみに、よく「(1)みたいにお父さんとお母さんの入れ替えを考えなくていいんですか？」と聞かれますが、それはしてはいけません。
なぜなら固定が解かれてしまうからです汗
例３．赤玉１つ、青玉２つ、黄玉３つを円形に並べる並べ方は何通りあるか？ただし、同じ色の玉は区別がつかず、回転して同じ並べ方になるものは同じものとする。
解答はコチラ！
今回の場合はどれを固定してもいい…わけではありません！
円順列は最終的に固定したモノ以外を順列として並べて考えます。
ただ、今回のように同じ色の玉の区別がつかないときに、例えば青玉１つを固定すると次のような問題が起きます。
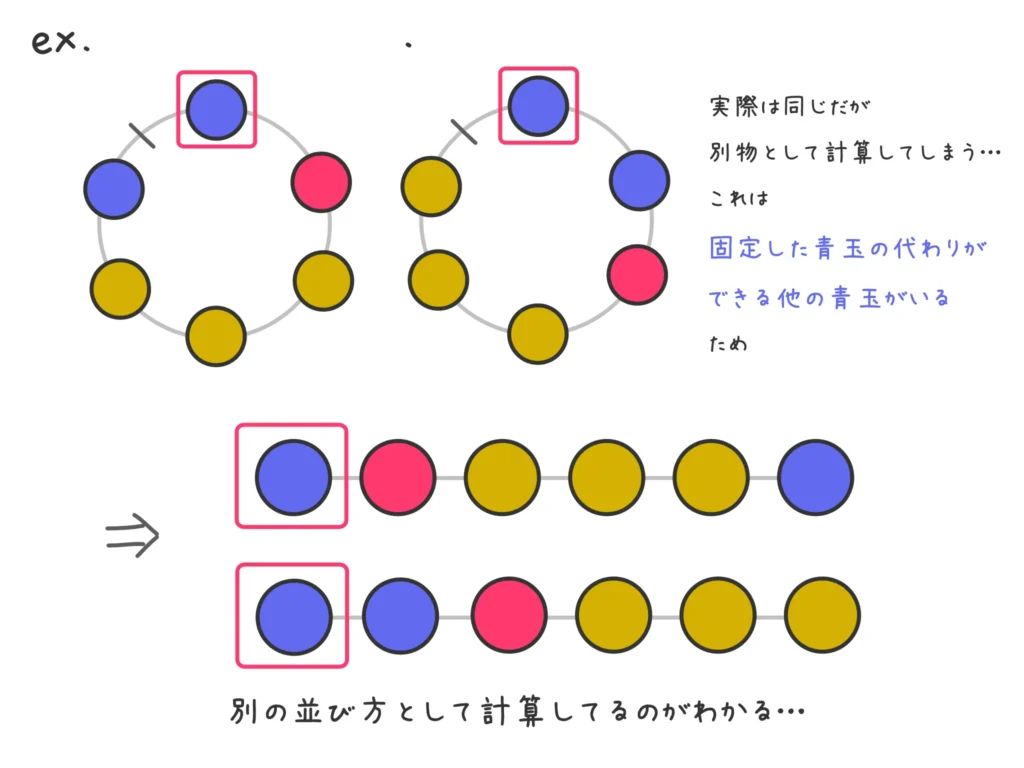
ということで、この中でも状況的に特別な（＝１個しかない）赤玉を固定します。
あとは青玉２つ、黄玉３つの計５つを、同じものを含むモノの並べ方で考えればよいので、
\(\displaystyle \frac{5!}{2! \cdot 3!} = \frac{5 \cdot 4 \cdot 3!}{2 \cdot 1 \cdot 3!} = 10\)（通り）…（答）
まとめ
円順列の計算方法についてでした。
「どれかを固定する」を押さえておけば大丈夫ですが、問題によってはその固定するモノもしっかり考える必要がある、というのは知っておいてください。
あわせて読みたい
C（組み合わせ）の性質とP（順列）との違いを具体例を用いて説明！
P（順列）に続いて教科書で習うC（組み合わせ）。このあたりを習い始めて「PとCはどう違うんだ？」とか「どういうときにPを使うのか、Cを使うのかわからん！」と疑問に…
ちょっと一息
数学をモチーフにしたオシャレなオリジナルグッズも販売中です！おかげさまで好評頂いてます！
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ！
また、このブログで活躍してるクマのLINEスタンプも販売しています！ぜひ一度見てみてください！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
