PR
順列(P)と階乗(!)【公式・どのような場面で使うかなど徹底解説!】

数学Aで習う順列。
 たろぅ
たろぅ順列(P)って、計算方法はわかるけどなんとなく使い所がわかりにくい…。
と思う人も多いトコロです。
この記事では順列(\(_{n}P_{r}\))の計算方法と実際使える場面を解説していきます。



\(_{n}C_{r}\)との違いがわからない、という人は次の記事で解説しているので、あわせて読んでみてください。

順列(P)と階乗(!)の計算方法



順列と階乗の計算は次のように行います。
\( _{n}P_{r} = n \cdot (n-1) \cdots (n-r+1) \)
\(n!=_{n}P_{n}=n\cdot(n-1)\cdots 2 \cdot 1\)
式にするとわかりにくいですが、\( _{n}P_{r}\)は\(n\)から1ずつ減らしながら\(r\)個掛けるという計算をします。
\(n!\)は\(_{n}P_{n}\)と計算方法は同じで、要は\(n\)から1ずつ減らしながら\(1\)になるまで(\(n\)個)掛けるという計算をします。



具体的に計算例をあげてみましょう。
例.
\( _{6}P_{4} = 6\cdot5 \cdot 4 \cdot 3=360 ←「6」から1ずつ減らしながら4個掛ける。\)
\( 5!=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120 \)
順列(P)の計算イメージ
「順列」はその名前の通り、順番を考慮した列、です。
なので、使うときには「先頭から、何通りの選択肢があるか?を考えて順に掛けていく」というイメージをもっておきましょう。
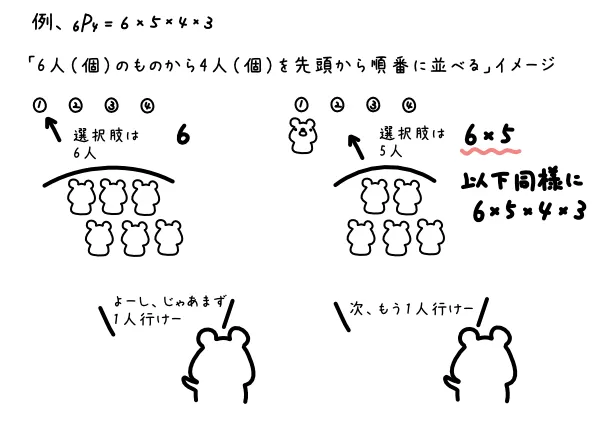




順列(P)の場合は、あんまり公式…という感じで扱わない方がスムーズに式を立てられるかもしれません。あくまでそういう表記だ、くらいに思っておきましょう。
前提として「選択肢がすべて区別できる」必要があります。
例えば「人」や「すべてが互いに異なる数字」「すべてが互いに異なる記号」などです。
区別がつかないものの並べ方、いわゆる「同じものを含む順列」の考え方は次の記事で説明していますので、あわせて御覧ください!


数学をモチーフにしたオシャレなオリジナルグッズも販売中です!おかげさまで好評頂いてます!
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ!
順列や階乗をどんなときに使うか
先ほど説明したように、使用する際のイメージを持っていれば、Pはあくまで表記上で「こういう書き方と計算をするんだよー」という感じです。
「Pってなんだ?わかんない!」という人は、「先頭から並べる計算してるんだな」というイメージを持った方がいいと思います。



このあと出てくる例のようにちょっと実践的な問題がわかんない、という人は「先頭から順に『何通りの選択肢があるのか』?」を意識してみてください。
あんまりPという記号に惑わされないようにしましょう!
順列を使う例「委員長などの係を選ぶ」
「先頭から何人か並べる」=「その順に係を割り当てていく」と考えます。



「この並び方や考え方をこう捉えればいいよね」というのは場合の数でよくやりますね。
例.6人から「委員長、副委員長、書記」を選ぶ。
「6人から3人選んで並べる」=「先頭から委員長→副委員長→書記と割り当てる」
と考えます。よって、\(_{6}P_{3}=6 \cdot 5 \cdot 4 =120\)(通り)、となります。
順列を使う例「文字や人を並べる」
これは順列の考えそのままですが、問題によっては色々な条件がついたりします。
「男子や女子がひとまとまりになる」「隣りあわないように並ぶ」「4桁の数字を作る」…など。
それぞれのケースで考え方のコツがありますので、一つ一つ押さえていきましょう。



場合の数・確率は条件のついているものから考えていくと上手く立式ができます!
例1.男子4人と女子3人が次のように並ぶ場合の数を求めよ。
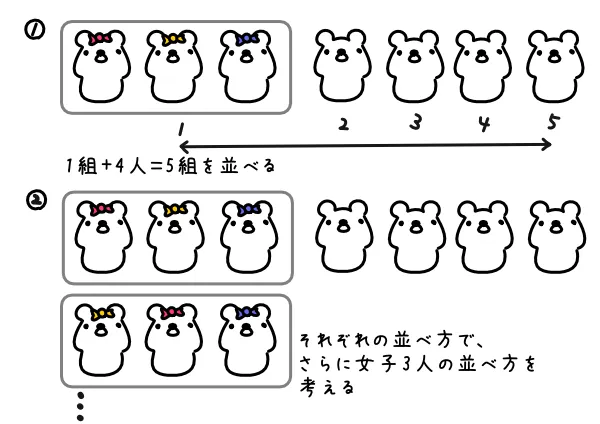
(1)女子3人が隣り合わせに並ぶ並び方。
(2)女子が隣り合わない並び方。
(1)
隣り合うパターンの場合、その離したくない女子3人を1組と見なして、1組+男子4人の5組を並べます(\(5!\)通り)。
さらに、それぞれのパターンで、女子3人を並べる並べ方を考えないといけません(\(3!\)通り)。
よって、\(5! \times 3! = 120 \times 6 = 720\)(通り)となります。

(2)
は、まず男子の間(両端を含む)5ヶ所のうち3ヶ所を選んで女子を並べます。これで、女子3人が隣り合わない、という条件を表現できます(\(_{5}P_{3}\)通り)。
さらに、それぞれのパターンで男子4人を並べる並び方を考ないといけません(\(4!\)通り)。
よって、\(5 \cdot 4 \cdot 3 \times 4!=1440\)(通り)となります。


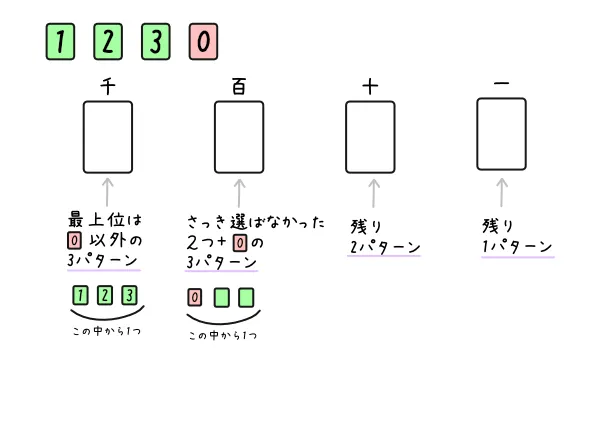
例2.0、1、2、3の4つの数字をそれぞれ1回ずつ使って4桁の数字を作るとき、いくつの数字ができるか。
ポイントは最上位(千の位)の数には「0」が入らない、というところです。
最上位に「0」が入ると4桁の数になりません。なので、最上位のパターン数は「1」「2」「3」の3通りとなります。
ただし、それ以降(百の位→十の位→一の位)は「0」が入ってもよいので、「0」も含めた、3通り→2通り→1通り、となります。
よって、\(3 \cdot 3 \cdot 2 \cdot 1 = 18\)(個)となります。

順列を使う例「円順列」
円順列も順列の一種ですが考え方に少しコツがいります。



別記事にしているので、そちらもぜひ見てみてください!


まとめ
階乗(!)はよく使いますが、正直順列(P)は使っても使わなくても問題ないと思います。
Pという記号にあまりとらわれず、基本的な考え方を押さえていきましょう。



場合の数はトライアンドエラーが重要です。考えながら手を動かして、失敗したらなぜ間違ったのか?を考えましょう(もしくは質問しましょう)。



はーい。







