PR
C(組み合わせ)の性質とP(順列)との違いを具体例を用いて説明!
P(順列)に続いて教科書で習うC(組み合わせ)。このあたりを習い始めて「PとCはどう違うんだ?」とか「どういうときにPを使うのか、Cを使うのかわからん!」と疑問に感じる人が増えてきます。
ここではCの基本的な計算方法から、Pとの違いまでを押さえていきます!
- C(組み合わせ)の知っておいた方がいい基本的な性質を押さえたい!
- P(順列)とC(組み合わせ)の使い方の違いを知りたい
C(組み合わせ)の基本
まずはC(組み合わせ)の基本的な計算や性質を押さえていきます。
Cの計算は以下のようになります。
$$ _{n}C_{r} = \frac{n \cdot (n-1) \cdots (n-r+1)}{r \cdot (r-1) \cdots 2 \cdot 1} $$
 せんせ
せんせ次のように計算方法をとらえるといいと思います。
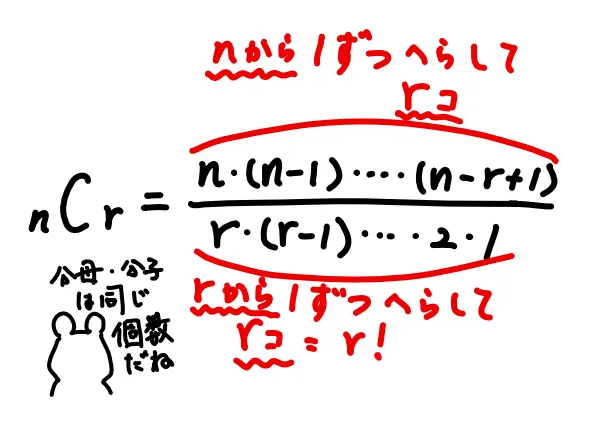
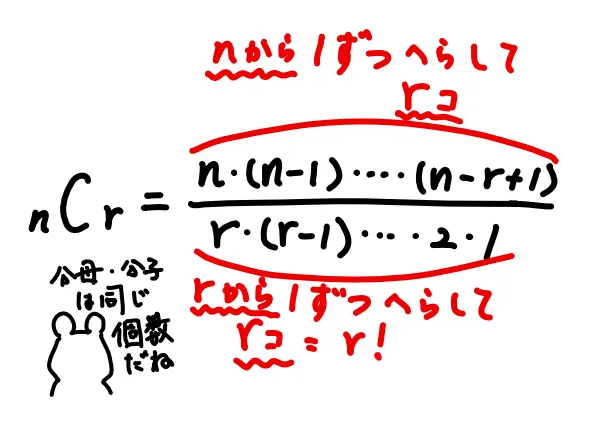
また、次の性質は計算上よく使います。
$$ _{n}C_{r} = _{n}C_{n-r} $$
\(n\)個のものから\(r\)個とってくる組み合わせは、\(n\)個のものから、とってこない方の\((n-r)\)個を選ぶのと一緒、という意味です。
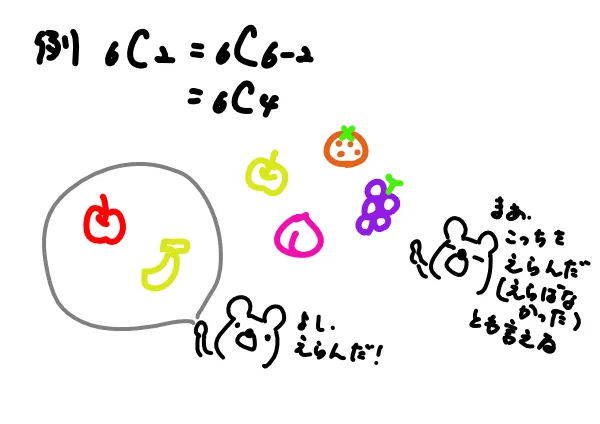
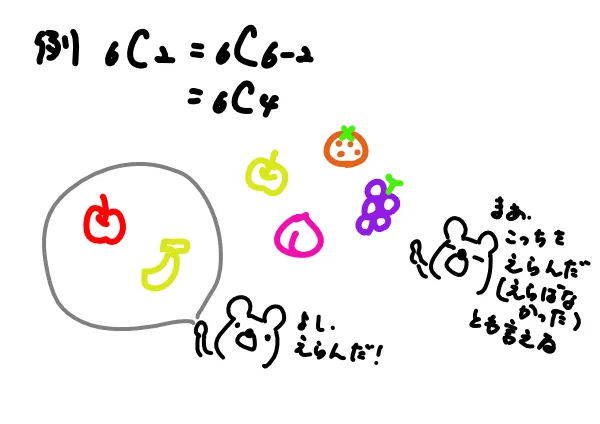
問題のレベルが上がってくると、次の!(階乗)を使った計算表現もよく使います。覚えておいた方がよいですね。
$$ _{n}C_{r} = \frac{n!}{r!(n-r)!} $$
P(順列)とC(組み合わせ)の違い



ん?そういえば、この間同じような計算をする公式を習ったな…。確か、P(順列)、だったっけ?何が違うんだろ?



確か、P(順列)は「何かを並べる」ようなときに使ったよね。



そうだったかな…そもそもP(順列)ってどう計算するんだっけ?


よくある疑問の一つに「P(順列)とC(組み合わせ)の違いがわからない」というものがあります。
結論から言うと
「順番を考える必要がある」→ P(順列)
「順番は考えていないor考える必要がない」→ C(組み合わせ)
という点が違います。



それでは、具体的に問題を考えながらPとCの違いを理解していきましょう。
P(順列)とC(組み合わせ)の違いの簡単な例
例1.1、2、3、4、5の数字から2つをとってきて2桁の数を作る場合の数は?
これはPを使います。計算方法は、
\(_5P_2=5 \cdot 4 =20(通り)\)
です。例えば、1と2を使う2桁の数でも「1、2(つまり12)」と「2、1(つまり21)」では違う数になるからです。
順番を考える必要があるのでP(順列)を使います。
例2.1、2、3、4、5の数字から2つをとってくる組み合わせの数は?
「組み合わせ」と言っているので、C(組み合わせ)を使います。もう少し丁寧に説明すると「順番を考慮する必要がないから」です。
\(_5C_2=\frac{5 \cdot 4}{2 \cdot 1} =10(通り)\)
となります。
先ほどと違って、1と2をとってくる組み合わせだけを考えるので「1、2」も「2、1」も組み合わせとしては同じものだと言えます。
順番を考える必要がないのでC(組み合わせ)を使います。
C(組み合わせ)がなぜこのような計算をするか、については次の記事に書いています。


P(順列)とC(組み合わせ)の違いの具体例



よし、わかった!「順番を考える」→P(順列)を使う。「順番を考える必要がない」→C(組み合わせ)を使うんだな!



その通り!それでは、PとCの違いを考えながら、より実践的な例を見ていきましょう。
問.リンゴ、バナナ、みかん、ぶどう、なし、ももが1つずつ、合計6個あります。それを次の様に分けるとき、Cを使って計算すべきものはどれでしょうか?
- 6個から3個とってくる場合の数。
- 6個から選んで、3人に1個ずつ配る場合の数。
- 2個を選んでA組に配り、残り4個から2個をB組に配る場合の数。
- 1個を選んでそれをニ割引に、残り5個から1個を選んでそれを三割引にする場合の数。
1の答え
これはCで計算します。3つとってくる果物はとってくるだけで、その中で順番をつけているわけではないからです。\(_6C_3\)で計算。
2の答え
これはCで計算しません。例えば同じ「リンゴ、バナナ、みかん」の組み合わせでも「Aさん→リンゴ、Bさん→バナナ、Cさん→みかん」と配るのと、「Aさん→リンゴ、Bさん→みかん、Cさん→バナナ」と配るのでは異なるものとして数えなければならないので、自然と順番を考えていることになります。よって、Cではなく\(_6P_3\)で計算すべきです。
3の答え
Cで計算します。2個選んでA組に配っても、その中で順番をつけているわけではないからです。その中でさらに人に配る、とかならPを使いますが。\(_6C_2 \cdot _4C_2\)で計算します。
4の答え
どちらでもいいです。「二割引になるものを選んで、そのあと三割引になるものを選ぶ」という考え方なら\(_6C_1 \cdot _5C_1\)。「二割引→三割引に順番に果物を割り当てていく」という考え方なら\(_6P_2\)です。自分がどう考えているかを正確に式にしていきましょう。
Pとの使い分けとして考えるべきポイントは、潜在的な考え方も含めて順番をつけて考えているか?という点です。割り当てるべき事柄を選んだ後、先頭から順に選んだものを割り当てる必要があると考えた場合はPを使いましょう。



ここまで理解できていれば大丈夫!
番外編 Cの面白い性質
Cには次の様な性質もあります。
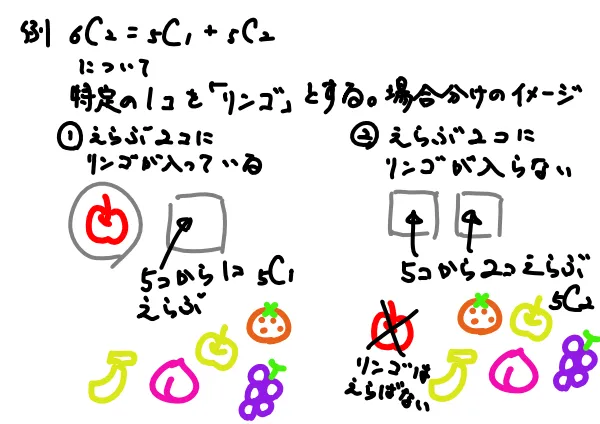
$$ _{n}C_{r} = _{n-1}C_{r-1}+_{n-1}C_{r} $$
これについて、参考書などの説明でよくある「特定の1つに注目して、それを含む組み合わせとそれを含まない組み合わせに分類して場合の数を求める」の意味がわかりにくいので、これも図で説明します。要は「場合分け」の考え方です。

まとめ
PとCの使い方の違いを説明しました。
PとCを使いわけるポイントは
順番を考えているかどうか?
です。
「そんなことわかってる」と思うかもしれませんが、実は立式をした時点で順番を考えているかどうか、が決まります。
そこを把握しないまま立式してしまうと、自分の意図に反して「順番をつけて考えた」計算になってしまったりします。
こちらも参考にして場合の数の理解を深めてもらえれば嬉しいです。





