PR
平方完成のやり方をわかりやすく説明！応用例も！
「平方完成」は高校数学で最初の山場、と言ってもいいでしょう。
「平方完成ってなんだったっけ？」という人にも、「なんで平方完成なんかするんじゃ！」という人にも、やり方からその本質まで、わかりやすく説明します。
平方完成は意外と応用例も多いので、うまく利用した例も紹介します。
目次
平方完成のやり方
平方完成とは、\(ax^2+bx+c\)を、「\( (xの1次式。しかもxの係数は1)^2 \)が現れる形に直す」という操作です。
たろぅ平方完成の方法って、イマイチ覚えきれないんですよね…。
せんせ結構複雑ですからね…。とりあえず、例題を解きながらやり方をおさらいしましょう。
例１．\( y=x^2-2x+2\)
例２．\( y=-x^2-x+1\)
例３．\(y=2x^2+4x+6\)
例４．\(y=3x^2+3x-1\)
例５．\(y=-3x^2+6ax-1\)
まずはやり方をおさらいです。
- \(x^2\)の係数が１じゃない場合は、\(x\)の係数と一緒にくくります。（まぁ、定数項も一緒にくくってもいいですけどね…。どうせ、あとでこの係数を展開するときに定数項部分は元に戻るだけなので無駄です。）
- \(x\)の係数を2で割って（\(\displaystyle \frac{b}{2a}\)とする）、\( (\quad)^2 \)の形を作り、\(\displaystyle (\frac{b}{2a})^2\)を引く。
- ①でくくった係数を\( (\quad)^2 \)の形を崩さないように展開し、定数項部分をまとめる。
\( ax^2+bx+c\)（ただし、\(a≠0\)とする）
\( \displaystyle = a(x^2+\frac{b}{a}x)+c \)（①）
\( \displaystyle = a \{ (x+\frac{b}{2a})^2-(\frac{b}{2a})^2 \}+c \)（②）
\( \displaystyle = a (x+\frac{b}{2a})^2-a\times \frac{b^2}{4a^2}+c = a (x+\frac{b}{2a})^2-\frac{b^2}{4a}+c\)（③）
補足．②の部分は何をしているのかというと、\( (x+a)^2 = x^2+2ax+a^2\)の展開公式を利用しているんですね。この展開公式の\(a^2\)を移項して左右入れ替えると、\( x^2+2ax = (x+a)^2-a^2\)となるので、結果\(x\)の係数を２で割って、その２乗を引くと、\( (x+a)^2 \)の形を使って表現ができる、という仕組みです。
たろぅ（\(a\)とか\(b\)とか、わかりにくい…）
せんせ「文字が多くてわかりにくい」って顔してますね。
先ほどの例で練習してみましょう。
残念ながら、ここは練習あるのみ！です。特に\(x^2\)が１でない場合は「最初にくくる→｛ ｝の中を平方完成→展開してまとめ」という形になり、マイナス計算がカラむ可能性もあるので計算ミスしやすいです。慣れるまで｛ ｝を省略しないようにしましょう。
例１．\( y=x^2-2x+2\)
例２．\( y=-x^2-x+1\)
例３．\(y=2x^2+4x+6\)
例４．\(y=3x^2+3x-1\)
例５．\(y=-3x^2+6ax-1\)
コツは「｛ ｝を使うこと」「その｛ ｝を展開するときに注意すること（特に符号）」ですね。
物事には間違いやすいポイント、というのがあります。何回かチャレンジしてみて、ミスが続くような場合は、きちんと原因まで押さえるクセをつけましょう。
たろぅしかし、なんで平方完成なんかするんだ？
これ以降は、平方完成の具体的な利用例をいくつか紹介していきます。
平方完成の利用「グラフの平行移動」
まぁ、これがメインですよね。
２次関数のグラフの平行移動の際に使います。つまり、
\( y=ax^2\)のグラフを\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動したグラフは、
\(y=a(x-p)^2+q\)
となります。このとき、頂点は\( (p,q)\)になります。
せんせ先ほどの例を見ていただければわかりますが、正にこの形に直す、という作業ですね！
さっきの例１であれば、\( y=x^2-2x+2=(x-1)^2-1^2+2 = (x-1)^2+1\)なので、グラフは次のようになります。
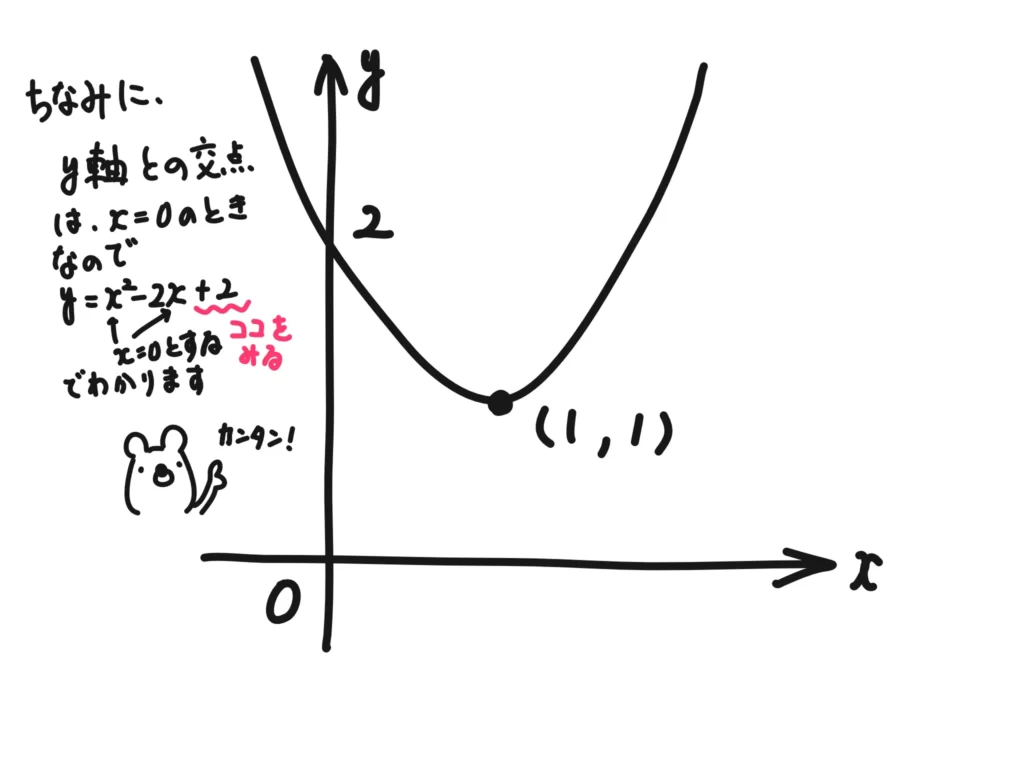
「なぜこのような頂点の読み方をするのか？」についてはこちらの記事もご覧ください。必見です！
あわせて読みたい
グラフの平行移動は全部同じ？平行移動はこれだけで完璧！
さて皆さん、いきなりですが問題です。 関数\(y=(x-1)^2+1\)が表すグラフの頂点の座標を求めよ。 答えは（1,1）ですね。 「簡単！」「あぁ、なんかあったなぁ…」「なん…
平方完成の利用「２乗したら０以上」
せんせそれでは次の問題を解いてください。
たろぅ平方完成の問題ですね！なんでも来てください！
問１．\(x^2+4x+6 \geq 0 \)
たろぅ平方完成の問題じゃない…。これは…２次不等式、だっけ？
せんせはい、解いてください。
たろぅう…確か、「=0」の方程式にして、解を求めるんだったよな…。
ん？これ、因数分解はできないな…。
\(x^2+4x+6 = 0 \)とすると、解の公式から
\( \displaystyle x = \frac{-4 \pm \sqrt{4^2-4 \cdot 1 \cdot 6}}{2 \cdot 1}\)（←本当は\(x\)の係数が２の倍数の場合の解の公式を使った方がよい）
\( \displaystyle x = \frac{-4 \pm \sqrt{-8}}{2}\)
たろぅ（あ、\( \sqrt{\quad}\)の中身が負になった。…計算ミスはしてないみたいだし。）解なしですね。
せんせぶっぶー！ぜんっぜんちがいます！！
たろぅ…。この感じ、ちょっと久しぶりかも。
確かに「=0」としたときの「方程式」としては解がないのですが、果たして不等式としての解はないのでしょうか？
こういうときに平方完成の出番ですね。
せんせ不等式の意味は「その式を満たす変数の範囲は？」というものです。それを踏まえて、もう一度先ほどの不等式を見てみましょう。
\(x^2+4x+6 \geq 0 \)
\( (x+2)^2-2^2+6 \geq 0 \)
\( (x+2)^2+4 \geq 0 \)
せんせさて、これを満たす\(x\)の値の範囲は？
たろぅんー…。なんで平方完成したんですか？
せんせ\( (x+2)^2+4 \geq 0 \)の形をよく見てください。
\( (x+2)^2 \)ってどんな値ですかね？正の値ですか？負の値ですか？
たろぅ\((\quad)^2\)ですから正の値ですよね？
せんせ正確には0以上ですが、そうですね。\(x\)が実数の場合\((\quad)^2\)は0以上の値になります。ということは、\( (x+2)^2+4 \)は0以上の値に4を足していることになりますよね。
たろぅなるほど、ということは\( (x+2)^2+4 \)は必ず正の値になりますね。
せんせつまり、\(x\)がどのような値だろうが、絶対、
\( (x+2)^2+4 \geq 0 \)が成り立ちますよね。
たろぅなるほど！
答えは「全ての値（\(x\)はどのような値でも成り立つ）」です。
\((\quad)^2\)は必ず0以上になる、というのと、\(x\)をその中に全てまとめることができる（２次の場合）、というのが重要ですね。
「実数を２乗すれば0以上になる」というのは「当たり前の条件」です。当たり前のこと、というのを意識することは重要です。
逆に「当たり前のこと」を疑うことも重要です。
「２乗してマイナスになる数（虚数）」というのもありますので、数学の話が進むにつれ「２乗したら0以上になるのは当たり前じゃないか」という常識も疑わなければならなくなります。
せんせ実生活でも「当たり前のことを意識すること」も「当たり前のことを当たり前と思わない」姿勢も重要ですね。
多変数関数の最小値
せんせそれでは次の問題を解いてください。
たろぅやばい、もうこの人、どんな問題を出してくるかわからんぞ…。
問．\( k = x^2-2xy+2y^2-4y+8\)の最小値を求めなさい。
たろぅ…文字が３つも出てきてるぅ。さっぱりわかんないぞ。
せんせ\(k\)は\( x^2-2xy+2y^2-4y+8\)をわかりやすくするために文字として置いただけですね。いわば優しさです。
問題の意味は、「\(x\)、\(y\)の２つの文字がそれぞれ勝手に動くので、そのときの\(k\)の最小値を求めてね」ということですね。
たろぅ（優しさ？）でも２つの文字が勝手に動かれたら、最小値なんかわかりませんよ。
こういうときも平方完成が活躍します。
多変数関数の基本的な考え方はそのうち別記事で説明したいと思います。が、とりあえず「\(x\)について平方完成」→「\(y\)について平方完成」という手順で式変形をしていきます。
（解）
\( k = x^2-2xy+2y^2-4y+8\)
\( = (x-y)^2-y^2+2y^2-4y+8\)（\(x\)について平方完成。つまり\(y\)は定数扱い。\(a\)とかと同じような感覚。）
\( = (x-y)^2+y^2-4y+8\)
\( = (x-y)^2+(y-2)^2-2^2+8\)（次は\(y\)について平方完成）
\( = (x-y)^2+(y-2)^2+4\)
せんせここまできたら、あとは先ほどの不等式と同じ考えですね。
\( (x-y)^2+(y-2)^2\)は\(x\)、\(y\)がどんな値でも0以上、つまり最小は0なので…。
たろぅなるほど、\( (x-y)^2+(y-2)^2+4\)は0以上のものに4を足しているから、最小値は\( (x-y)^2+(y-2)^2=0\)のとき、4ですね。
答えは\( (x-y)^2+(y-2)^2=0\)つまり、\( (x-y)^2=0\)かつ\((y-2)^2=0\)→\(x=y=2\)のとき、最小値4
せんせ平方完成したら、2次式を\((\quad)^2\)の形にまとめることができるのがポイントですね。
数学IIの不等式の証明でも使ったりするので、用途は意外と幅広いです。
あわせて読みたい
等式・不等式の証明の「正しい書き方」へのコツ
証明…響きがイヤですね。 実際に「証明」と聞いて「うわー…なんか色々書かないといけないやつでしょ？書き方も細かいし、イヤ！嫌い！」という人も（たくさん）いると思…
まとめ
平方完成のやり方と使用例を説明しました。
平方完成の使用上のポイントとしては、
- ２次関数のグラフを描くときに使う
- ２次式を\(a(１次式)^2+(定数)\)の形に直すことで特に「\((\quad)^2\)が0以上」という性質を上手く使う。
数学IIの円の方程式や数学IIIの楕円の方程式、式の証明や、上手く使えば関数の値の範囲を求めたりなど、意外と応用範囲が広い技術ですので、しっかりとマスターしてください。
あわせて読みたい
面白くてオススメの数学本・マンガ
最近よく「オススメの数学の本はありますか？」という質問を受けます。 正直、あんまり本は読まないのですが、これまで読んできた中で「これは面白い！」というオススメ…
ちょっと一息
このブログで活躍してるクマのLINEスタンプもあります！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
