PR
微分とは?わかりやすく説明【これを知ってから教科書を勉強しよう!】

微分…「高校で習ったけど…なんだっけ?」とか「今勉強してるけどよくわかんない」という人もいると思います。
そんな人に「微分って、結局何?」という話をわかりやすく説明していきます。
 せんせ
せんせ今回はあまり小話は無しでサクッと説明していきましょう。
微分とは?結局なんなの?
結論から言うと「その瞬間の変化率」(…という関数)を求めることです。
「なんのこっちゃ!?そんなのなんの役に立つんじゃい!」と思うかもしれませんが、少し例をあげて見てみましょう。
微分でグラフをかいてみよう
突然ですが、次の関数のグラフをかいてください、と言われたらどうしますか?
\(\displaystyle y = \frac{x^2-x+2}{x+1} \)
数学Ⅲの微分を習った人は「式変形して、定義域確認して、微分して、増減表かいて…」と思うかもしれません。
ですが、それはまぁテクニカルな話です。
「微分(というテクニック)を知らなければどうしたらいいだろう?」というところから出発して、微分の本質的な意味を考えていきましょう。
さて、さきほど「微分とはその瞬間の変化率を求めること」と言いましたが、ここで関数\(f(x)\)について考えてみましょう。
この関数\(f(x)\)のグラフをかきたい、と思ったときにこの「瞬間の変化率を求める」というのが有効です。
「瞬間の変化率」は「そのとき(その\(x\)のとき)どっち方向に(\(y\)方向の正か負か)どれだけ進むか」という意味です。これを考えたときに、関数\(f(x)\)のグラフ\(y=f(x)\)は次のようにして概形をかくことができます。
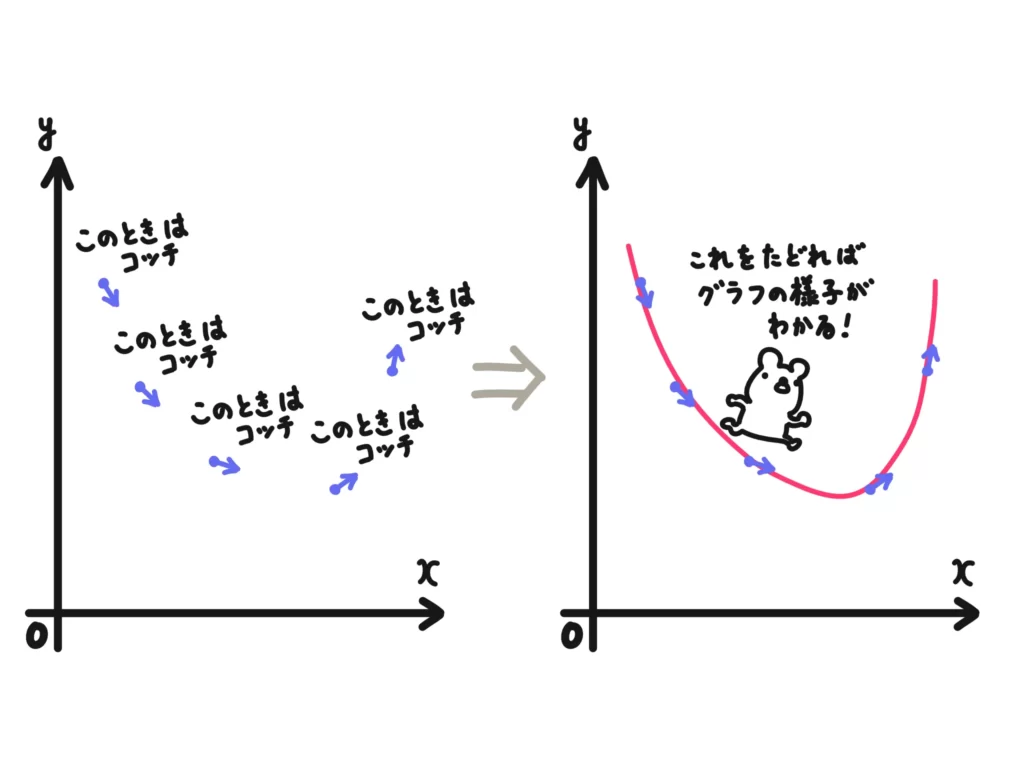




最低限「\(y\)方向のどっちのに進むか」がわかればそれを辿ってグラフの概形をかくことができますね。
「その瞬間の変化率」を求めて調べることでグラフなどの振る舞いを知ることができる、というのが微分の大きな意義です。
先ほどのグラフの概形のかき方はこちら
ちょっとテクニカルな話になりますが、数学IIIの微分を使ってグラフをかくとき、以下の手順に注意して解いてください。



いきなり微分しちゃダメです!
- 定義域を押さえる。分数関数(分母\(\neq 0\))や無理関数(ルートの中身\(\geq 0\))など、関数の形から縛られる定義域に注意。
- (対称性を調べる。関数が\(x\)軸対称や原点対称であることがわかれば作業がほぼ半分で済む。)
- (分数関数は(分母の次数)\(\geq\)(分子の次数)になるように変形しておく。この形だと微分計算しやすい+漸近線を調べやすい。)
- 微分して増減表をかく。定義域に注意!
- 極限(\(x \rightarrow \pm \infty\)と\(x \rightarrow \)(定義域の切れ目))を調べる。
- グラフをかく。
②は必須ではないですが、準必須の作業です。サラッと対称性を調べることができれば、作業を約半分に減らすことができます。微分計算は面倒なことが多いのでその作業を半分に減らせると時間短縮、計算ミスを減らすことができます。
(解答)
\(\displaystyle y = \frac{x^2-x+2}{x+1} \)
(分母)\(\neq 0\)なので\(x\neq -1\)
\(\displaystyle y = \frac{x^2-x+2}{x+1} = x-2 + \frac{4}{x+1}\)
より、
\(\displaystyle y’ = 1 + \frac{-4}{(x+1)^2}=\frac{(x+1)^2-4}{(x+1)^2}=\frac{(x-1)(x+3)}{(x+1)^2}\)
\(y’=0\)とすると、\(x=-3,1\)。よって増減表は次のようになる。
\begin{array}{|c|ccccccc|}
\hline
x & \cdots & -3 & \cdots & -1 & \cdots & 1 & \cdots \\
\hline
y’ & + & 0 & – & × & – & 0 & + \\
\hline
y & \nearrow & -7 & \searrow & × & \searrow & 1 & \nearrow \\
\hline
\end{array}
ここで、\( \displaystyle \lim_{ x \to -1+0 } \left( x-2 + \frac{4}{x+1} \right) = \infty \)、
\( \displaystyle \lim_{ x \to -1-0 } \left( x-2 + \frac{4}{x+1} \right) = -\infty \)
\( \displaystyle \lim_{ x \to \pm \infty} \left\{ y-(x-2) \right\} = \lim_{ x \to \pm \infty} \left( \frac{4}{x+1} \right)=0\) なので、
\(x=-1\)と\(y=x-2\)は漸近線。
よって、\(\displaystyle y = \frac{x^2-x+2}{x+1} \)のグラフの概形は次のようになる。
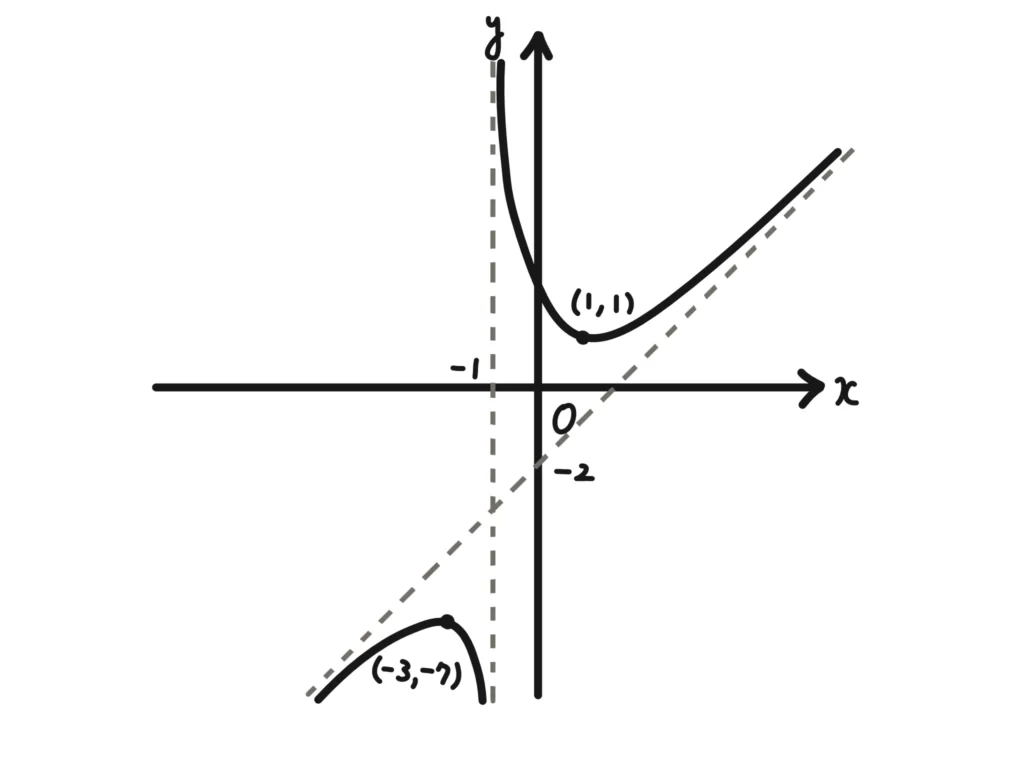

微分の定義
ここまで知っておいて、教科書の微分の話を進めるとわかりやすいと思います。
では、どうやって「その瞬間の変化率」を求めていくか?を解説していきます。
簡単に説明すると、「ある区間の平均変化率を求めておいて、その区間を限りなく小さくせばめていく」ことで「その瞬間の変化率」を求めていきます。
平均変化率
関数\(f(x)\)の\(x=a \rightarrow x=a+h\)までの平均変化率は、
「関数\(f(x)\)の\(x=a \rightarrow x=a+h\)までの平均変化率」
\(\displaystyle \frac{f(a+h)-f(a)}{(a+h)-a}=\frac{f(a+h)-f(a)}{h}\)
となります。これを元に「その瞬間の変化率」を求めていきます。
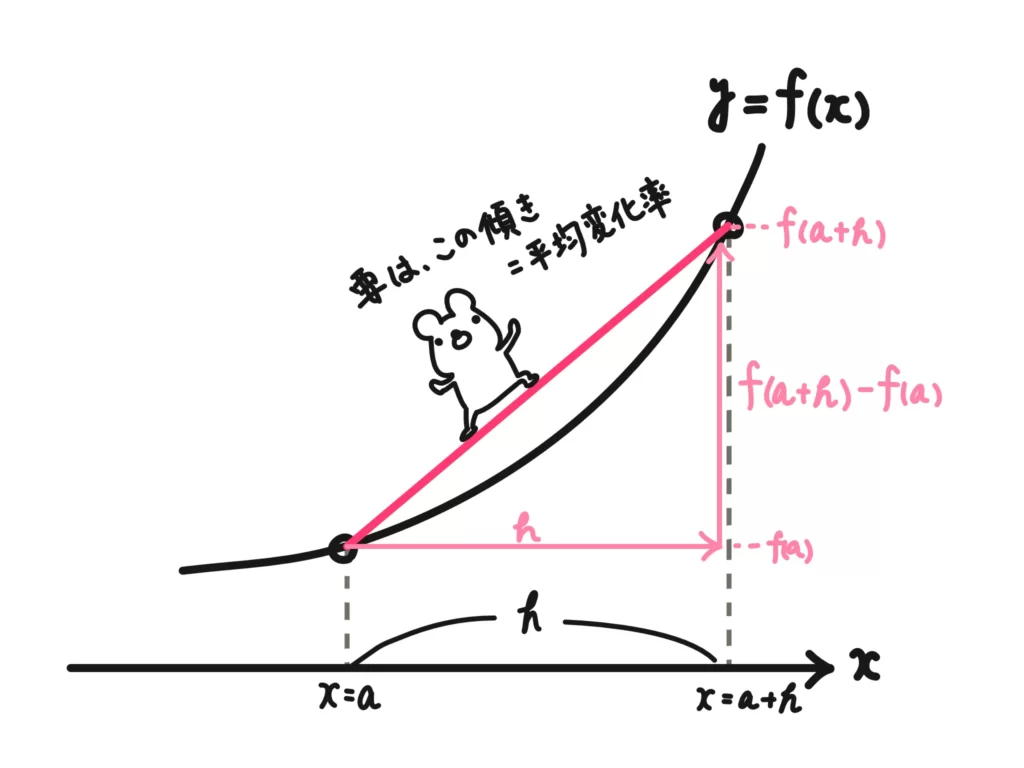

今、ちょっと変わった区間の取り方をしていることがわかると思います。上の図を見てくれればわかると思いますが、\(x=a \rightarrow x=a+h\)の\(h\)は区間の幅を表しています。
ですので、仕上げはこの\(h\)を限りなく0に近づけていきます。
このとき、極限という考え方を使います。
極限って?



ちょっとだけ、極限という考え方について説明します。
「極限」
関数\(f(x)\)の\(x\)を限りなく\(a\)に近づけていくとき、\(f(x)\)が\(\alpha\)に近づくとするとき
\(\displaystyle \lim_{ x \to a } f(x) = \alpha\)
とかく。



ポイントは、\(\alpha\)は「近づく値」だということです。
ちょっとだけ例もあげておきます。
例1.\( \displaystyle \lim_{x \to 5}(x+2)=7\)
例2.\( \displaystyle \lim_{h \to 0}(h^2+h-1)=-1\)
「代入してるだけじゃない?」と思うかもしれません。確かに結果だけ見れば代入しているように見えますが、これはあくまで「\(x\)(や他の変数)がある値に限りなく近づいたときに近づく値は?」という意味合いです。
意味が違う、という点には注意しておいてください。
話を戻して「瞬間の変化率」を求めよう



さて、話を戻して、「関数\(f(x)\)の\(x=a \rightarrow x=a+h\)までの平均変化率」は次のように表せるのでした。
\(\displaystyle \frac{f(a+h)-f(a)}{h}\)
この区間を限りなくせばめていくので、「区間の幅」の意味である\(h\)を極限を使って限りなく0に近づけていきます。
こうして求めた値を関数\(f(x)\)の\(x=a\)における微分係数といい、\(f’(a)\)と表します。
「関数\(f(x)\)の\(x=a\)における微分係数f'(a)」
\(\displaystyle f'(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}\)\)
とする。
この\(f'(a)\)がずっと言っている「その瞬間(\(x=a\))の変化率」になります。
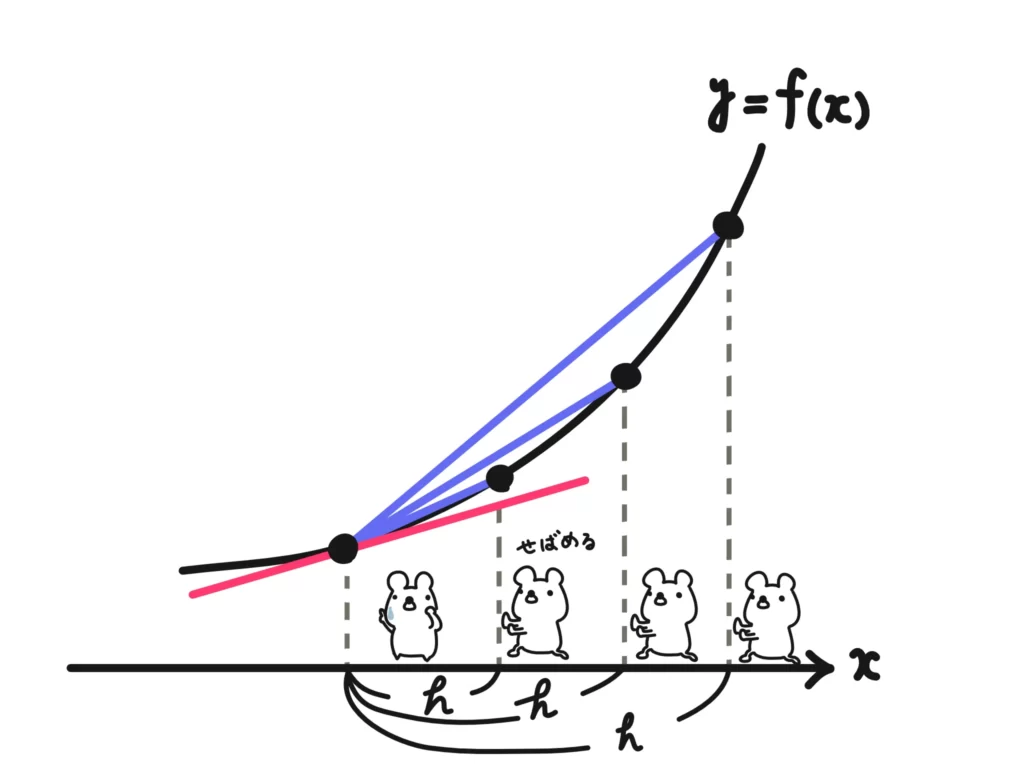

この、「その瞬間(\(x=a\))の変化率である微分係数\(f'(a)\)」にはもう一つ重要な側面があります。それは\(f'(a)\)は\(x=a\)における\(f(x)\)の接線の傾きになる、ということです。
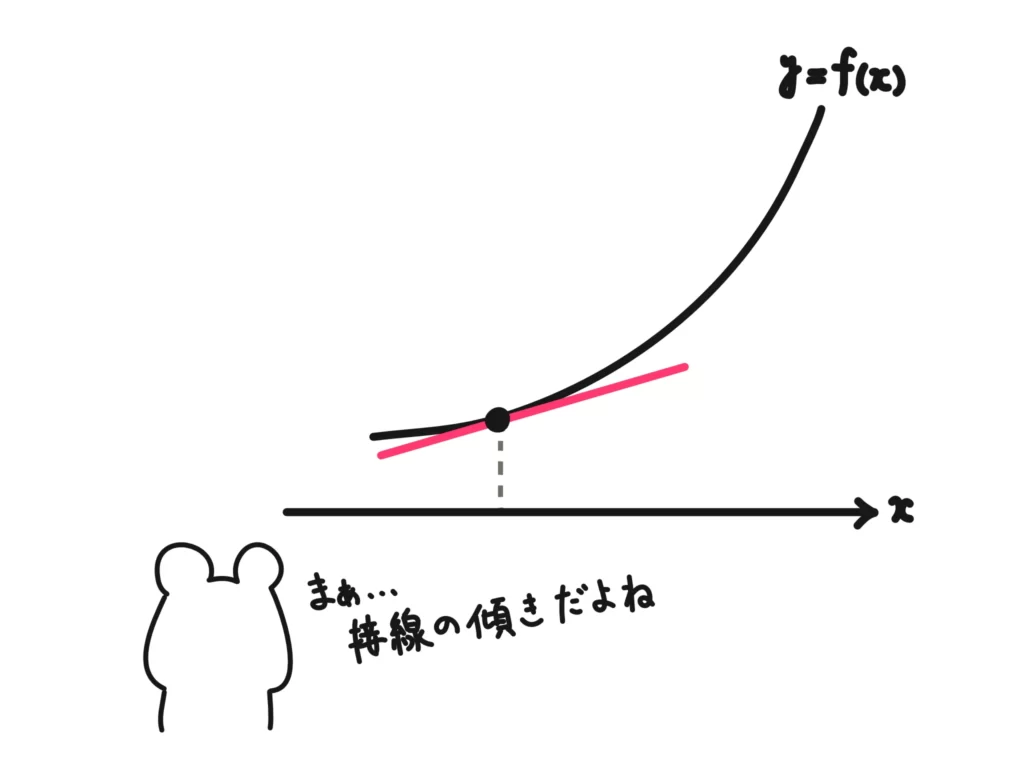




微分係数\(f'(a)\)は\(x=a\)における\(f(x)\)の接線の傾き…これはよく使うので押さえておきましょう!
ただ、あくまで\(f'(a)\)は「その瞬間の変化率」を表している、という意識を持っておきましょう。
その瞬間だけでは…微分して関数にしよう
ここまでのアイディアはいいのですが、このままだと実はちょっと面倒です。
だって、「その瞬間の変化率」をいちいち微分係数\(f'(a)\)の定義を使って求めないといけないんですから。



\(x=-1\)、\(x=0\)、\(x=2\)、\(x=\sqrt{5}\)、\(\displaystyle x=\frac{5}{2}\)のときの微分係数を求めて!
とか言われたら、面倒ですよね?
そこで、この微分係数(=その瞬間の変化率)を関数にしたものをあらかじめ計算しておきます。そうすれば、今の話でも\(x=-1\)、\(x=0\)、\(x=2\)、\(x=\sqrt{5}\)、\(\displaystyle x=\frac{5}{2}\)をそれぞれ代入すれば求めることができて便利ですよね。



グラフの概形をかくためにも、関数の形にしておかないと全ての定義域内での「瞬間の変化率」は調べられません。
ということで、微分係数を関数にしたもの(語弊がありますが)を準備します。この関数を導関数といいます。
「導関数の定義」
\(\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\)
微分係数の\(a \rightarrow x\)にしただけで形は一緒ですが、\(a\)はある瞬間\(x=a\)(つまり定数)、\(x\)は変数ですので、意味合いが全く異なります。
この導関数\(f’(x)\)を求めることを「関数\(f(x)\)を微分する」といいます。



この\(f’(x)\)を上手く利用することで、接線を求めたりグラフの概形をかけたりするのですが、今回は微分の基本ですのでそのあたりはまた別の機会に説明したいと思います。
まとめ
微分は、特に教科書の流れを何も言われずに最初から勉強していると、「いったいなぜこんなことをしているのだろう?」となりがちな分野です。
まずは「その瞬間の変化率」を求めているんだ、ということを理解しましょう。
話は変わりますが、昔、酔っぱらった親戚に「微分積分がなんの役に立つんだ?」と言われたことがあります。ですが、実は気づいていないだけで微分・積分は身近に沢山転がってます。そのときは「ははは」と言っておきましたが。
「その瞬間の変化率」を利用するので、
天気予報、株価予測、などの予測系には大体使われていますし、自動車の速さを求めたり、橋の設計や人工衛星の軌道計算にも使われています。最近の流行りでいうと、人工知能(AI)のプログラミングにも使われています。
ですので、実際に微分・積分の計算をするか?は別として、考え方の概要だけでも掴んでおけば「あぁ、こういうことしているんだ」というのがわかるのではないでしょうか。







