PR
確率統計の分散とは?求め方や変数変換aX+bでどうなるか説明
確率統計の分散はデータの分析で扱った分散と、意味としてはほぼ同じです。

意味合いとしては、データの分析と同じく「平均からどれくらい散らばっているのか?」を示すのですが、計算方法はちょっと異なります。
加えて、この後「複数の確率変数の和の分散がどうなるか?」という議論の土台となるので、ここで基本を押さえておきましょう。
確率統計における分散とは?求め方を説明
 たろぅ
たろぅせんせい、今日確率統計で「分散」を習ったんですけど、これって以前データの分析でやった「分散」とは違うんですか?



いやいや、確率統計の話なので計算方法は違いますけど、意味合いとしては同じですよ。



あ、そうなんですね。ありがとうございましたぁ。



まてぃ!確率統計の分散計算は、この後「確率変数の和の分散」→「二項定理の分散」→…と繋がっていく大事な話なのだ!
適当に流そうとするんじゃない!



(しまった、また余計なこと聞いたかな…。)
確率統計における分散と標準偏差は次のように求めることができます。
分散と標準偏差の求め方
確率変数\(X\)の確率分布が次のように与えられているとする。
| \(X\) | \(x_1\) | \(x_2\) | \(\cdots\) | \(x_n\) | 計 |
| \(P(X)\) | \(p_1\) | \(p_2\) | \(\cdots\) | \(p_n\) | 1 |
確率変数\(X\)の期待値\(E(X)=m\)とすると、分散\(V(X)\)は
\(\displaystyle V(X)= (x_1-m)^2 p_1+ (x_2-m)^2 p_2+\cdots+ (x_n-m)^2p_n \)
となる。
また、
\(\displaystyle V(X)= E(X^2)-\{E(X)\}^2\)…※
でも求めることができる。
また、標準偏差\( \sigma (X) \)は
\( \sigma (X) = \sqrt{V(X)} \)
となる。
(※の証明)
\( V(X)= (x_1-m)^2p_1+ (x_2-m)^2p_2+\cdots+ (x_n-m)^2p_n \)
\( \quad = ( x_1^2-2x_1m+m^2)p_1 + ( x_2^2-2x_2m+m^2)p_2+\cdots \)
\( \quad\quad + ( x_n^2-2x_nm+m^2)p_n \)
\( \quad = ( x_1^2p_1+\cdots+ x_n^2p_n)-2m ( x_1p_1+\cdots+ x_np_n)\)
\( \quad\quad +(p_1 + \cdots +p_n)m^2\}\)
\( \quad = E(X^2) -2m \cdot m + 1 \cdot m^2\)
\( \quad = E(X^2) -m^2= E(X^2)- \{ E(X) \}^2\)(終)



「データの分析」でも※に相当する分散の計算方法がありますね。
実は「データの分析」では※はあまり活躍しないのですが、確率統計の分散では※の計算はちょくちょく活躍します。
分散の計算例



それでは例題を出すので、実際に分散の計算してみましょう。
例.コインを3枚投げたとき、表が出る枚数を\(X\)とする。\(X\)の分散を求めよ。



まずは確率分布から作っていきましょう。
(解)
表の枚数が0枚となる確率は、 \(\displaystyle \left( \frac{1}{2} \right)^3=\frac{1}{8}\)
表の枚数が1枚となる確率は、 \(\displaystyle _3C_1 \left( \frac{1}{2} \right)\left( \frac{1}{2} \right)^2=\frac{3}{8}\)
表の枚数が2枚となる確率は、 \(\displaystyle _3C_2 \left( \frac{1}{2} \right)^2\left( \frac{1}{2} \right)=\frac{3}{8}\)
表の枚数が3枚となる確率は、 \(\displaystyle \left( \frac{1}{2} \right)^3=\frac{1}{8}\)
よって、確率分布は次のようになる。
| \(X\) | 0 | 1 | 2 | 3 | 計 |
| \(P(X)\) | \(\displaystyle \frac{1}{8}\) | \(\displaystyle \frac{3}{8}\) | \(\displaystyle \frac{3}{8}\) | \(\displaystyle \frac{1}{8}\) | 1 |
\(\displaystyle E(X)=0 \cdot \frac{1}{8}+1 \cdot \frac{3}{8}+2 \cdot \frac{3}{8}+3 \cdot \frac{1}{8}=\frac{3}{2}\)
\(\displaystyle E(X^2)=0^2 \cdot \frac{1}{8}+1^2 \cdot \frac{3}{8}+2^2 \cdot \frac{3}{8}+3^2 \cdot \frac{1}{8}=3\)
よって、分散\(V(X)\)は
\(\displaystyle V(X)=E(X^2)-\{ E(X) \}^2 = 3-\left( \frac{3}{2} \right)^2=\frac{3}{4} \)…(答)



定義の方で計算しないんですね…。



確率の場合は、期待値(平均)が綺麗な値になることが少ないんですよね。そうすると、(変数ー期待値\()^2\)の計算が大変になるんです。
(定義に従って分散を計算してみると…)
\(\displaystyle V(X)=\left(0-\frac{3}{2}\right)^2\frac{1}{8}+\left(1-\frac{3}{2}\right)^2\frac{3}{8}\)
\(\displaystyle \quad \quad +\left(2-\frac{3}{2}\right)^2\frac{3}{8}+\left(3-\frac{3}{2}\right)^2\frac{1}{8}\)
\(\displaystyle \quad =\frac{9}{4} \cdot \frac{1}{8}+\frac{1}{4} \cdot\frac{3}{8}+\frac{1}{4} \cdot\frac{3}{8}+\frac{9}{4} \cdot \frac{1}{8}=\frac{3}{4}\)



ちょっと面倒ですね。



確率の場合は、期待値(平均)があまり綺麗な値にならず、逆に確率変数は2乗するのがそこまで大変じゃないことが多いので、
計算でも証明でも\(V(X)=E(X^2)-\{E(X)\}^2\)を使うことが多いです。
数学をモチーフにしたオシャレなオリジナルグッズも販売中です!おかげさまで好評頂いてます!
普段使いしやすいグッズです。ステッカーやマグカップも人気ですよ!
確率変数の変換aX+bで分散はどうなる?
データの分析においては、分散は「平均からの散らばり具合」になります。
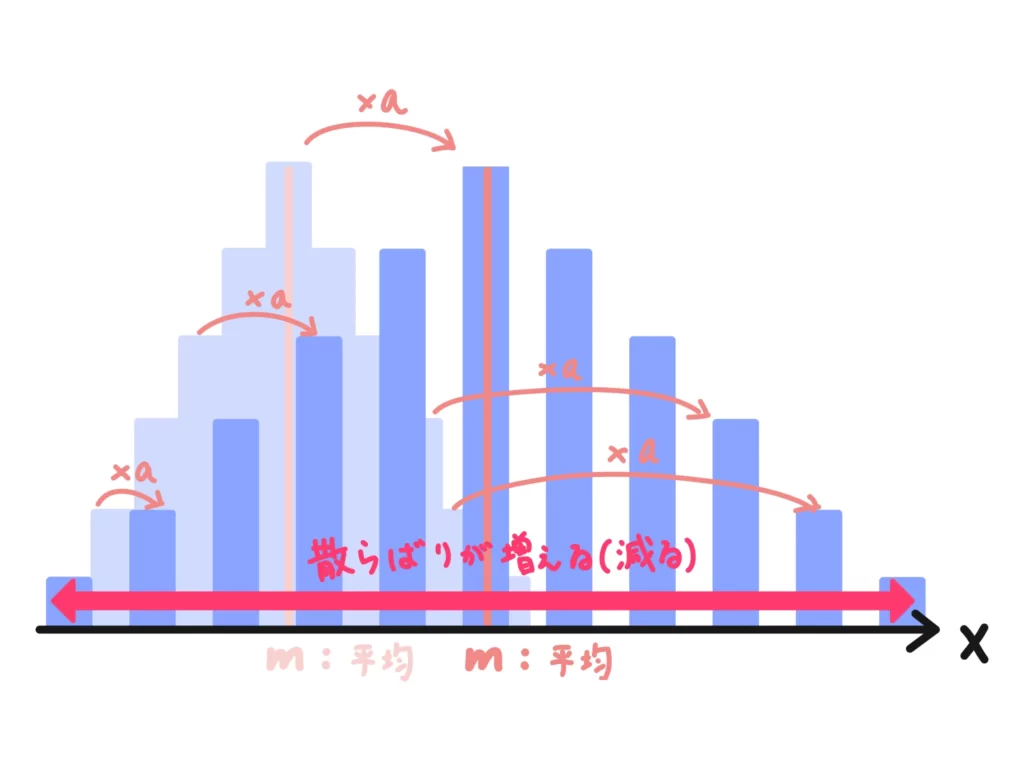
確率統計においても分散は「平均(=期待値)からの散らばり具合」になります。イメージ的には次のようになります。
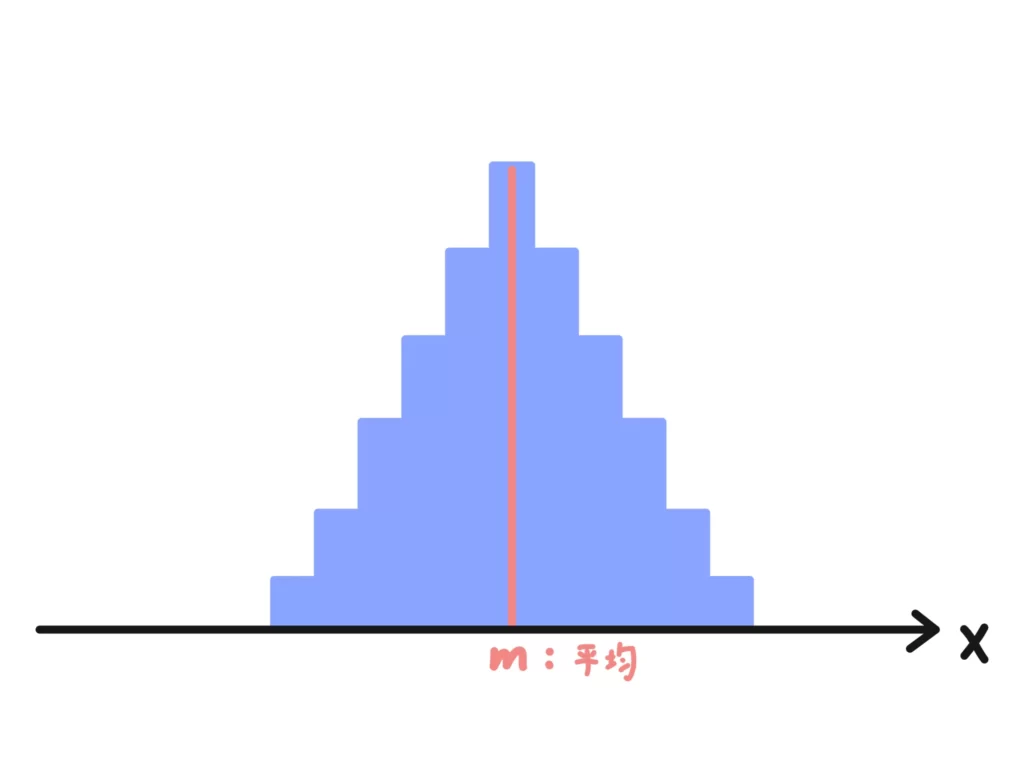

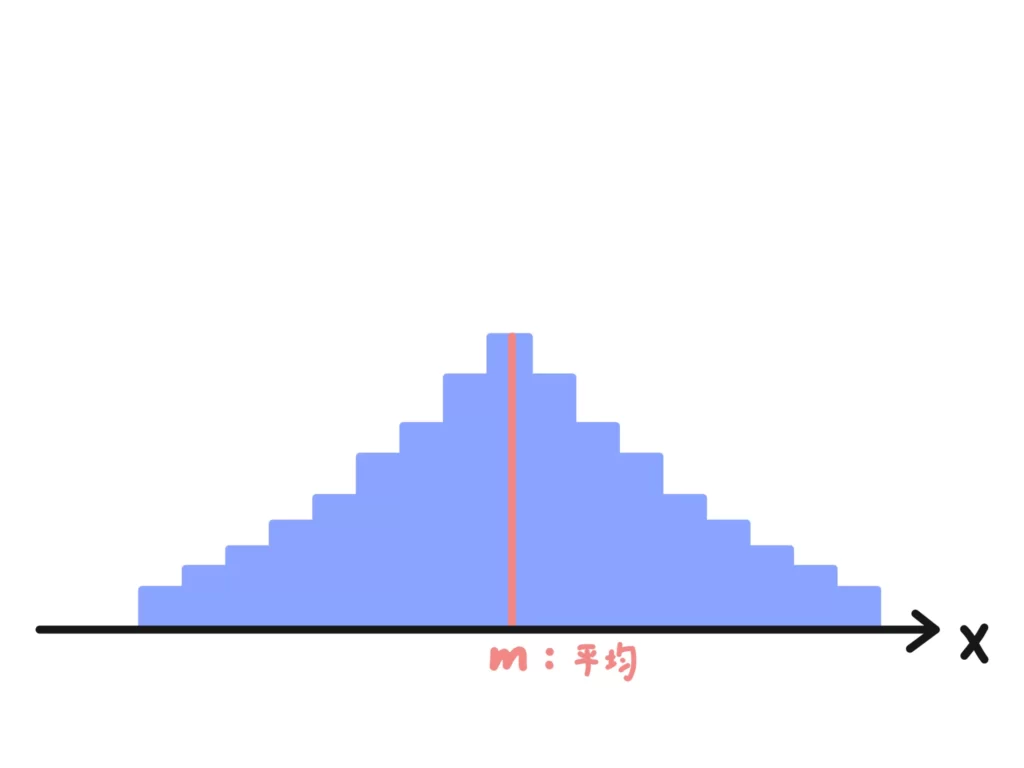




このように確率分布ををグラフのように表現することもあります。この後出てくる正規分布などでよくみられる図ですね。
図のように、分散が大きければ「平均からの散らばり具合」が大きく(裾が広がった図)になります。
では、確率変数の変換で\(X\)を\(aX+b\)にしたらどうなるか、というと、
確率変数\(X\)の分散を\(V(X)\)とする。\(X\)を\(aX+b\)に変換すると、分散\(V(aX+b)\)は
\(V(aX+b)=a^2V(X)\)
となる。
分散はデータの分析の分散と同じ意味合いですので、こちらで解説したように分散は\(aX+b\)の\(+b\)の影響は受けません。


\(+b\)は各確率変数に\(b\)を加えるという操作なので、分散(=散らばり)に影響しないからです。
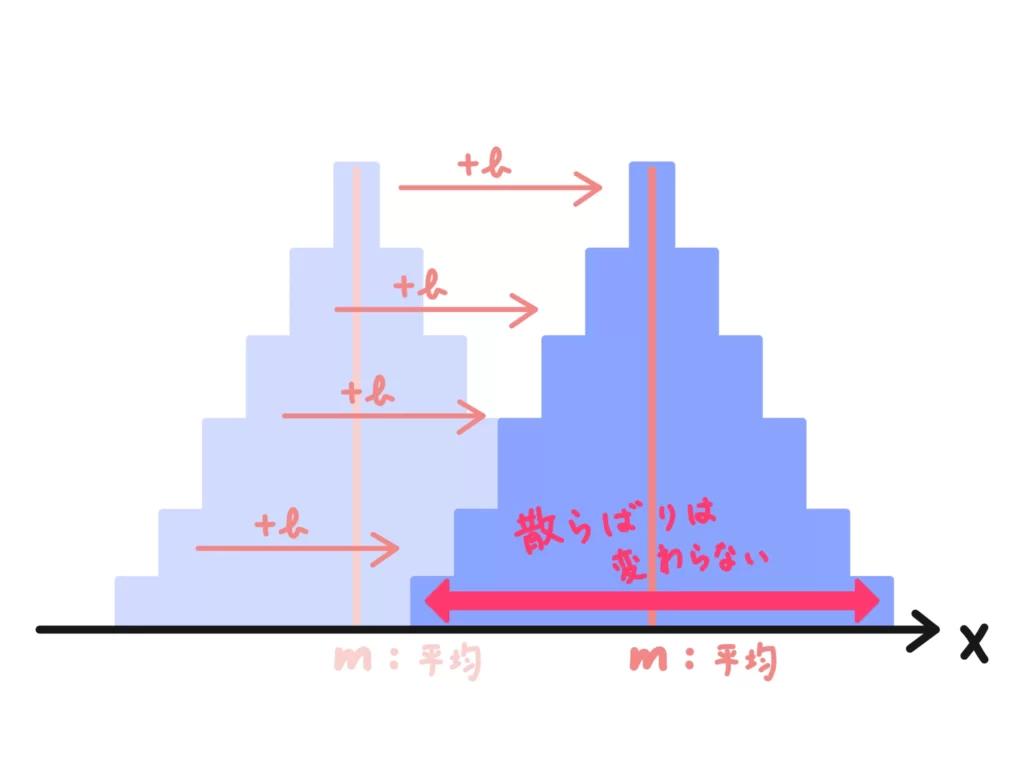

\(aX+b\)の\(\times a\)については、各確率変数に\(a\)を掛ける操作なので「0に近いものはそこまで0から離れず、遠いものはより遠く」に確率変数が配置され直す、と思ってください。
つまり、分散(=散らばり)は大きく(小さく)なります。
結果としては、\(a^2V(X)\)のように、元の分散に2乗して掛けることになります。




イメージ的にはこんな感じですね。
証明もしておきましょう。
(証)
確率変数\(X\)の期待値\(E(X)=m\)とする。\(X\)を\(aX+b\)と変換すると、期待値は\(E(aX+b)=am+b\)となる。(説明はこちらをご覧ください。この後、計算過程でも期待値の変数変換を使います。)
ここで、分散は「(変数ー期待値\()^2\)の期待値」ともいえるので、\(V(X)=E((X-m)^2)\)、
\(V(aX+b)=E( \{ aX+b-(am+b) \}^2 )\)と計算できる。
\(V(aX+b)=E( \{ aX+b-(am+b) \}^2 )=E( \{a(X-m)\}^2 )\)
\( \quad = E(a^2(X-m)^2)\)
\( \quad = a^2E((X-m)^2)\)
\( \quad = a^2V(X)\)(終)
まとめ
分散の基本と例題と変数変換について説明しました。
分散は期待値(平均)と同様に、データの分析や確率統計の基本です。
今後の応用にもつながってくるのでしっかりと計算できるようにしておきましょう。










