ベクトルの成分表示とは？【大きさ・内積…意味や計算方法総まとめ】

2023年10月22日

ベクトルは便利で重要な考え方ですが、苦手な人が多い分野でもあります。

原因は「イメージ」と「その場での思考」が重要だからです。

たろぅ

その状況に応じた対応って苦手…。

ですが、その分覚えることも少ないですし、基本的なイメージをしっかりと掴むことができればあとはちょっと練習するだけでベクトルの理解はかなり深まります。

せんせ

要は最初の本質部分が大事！
「ベクトルは感覚だ！」

この記事では、ベクトルの成分表示について考え方や計算方法の説明をしていきます。

ベクトルの成分表示とは？

せんせ

ドキドキ！数学的常識感覚ク〜イズ！！

はなこ

…。

たろぅ

…。

せんせ

前回説明した「ベクトルの分解」は覚えてますかね？

たろぅ

うん…まぁ…。

せんせ

では問題です！ベクトルの分解で主張したいことの一つとして「平面上のどんなベクトルでも、２つのベクトル（基底ベクトル）の和で表すことができる」というものがありましたが…、
この基底ベクトルは零ベクトルでもなく、平行でもないならどんな２つのベクトルでもOKでした。

はなこ

テキトーなベクトルでも２つあれば、それを伸ばしたりして足すことでどんなベクトルも表せるよ、ってことでしたよね。

せんせ

そういうこと。では、どんな２つのベクトルでもいいなら…
あなたならどんな２つのベクトルを選びますか！？方向は？大きさは？

たろぅ

えー…別になんでもいいなら考えるだけ無駄じゃないですか…。

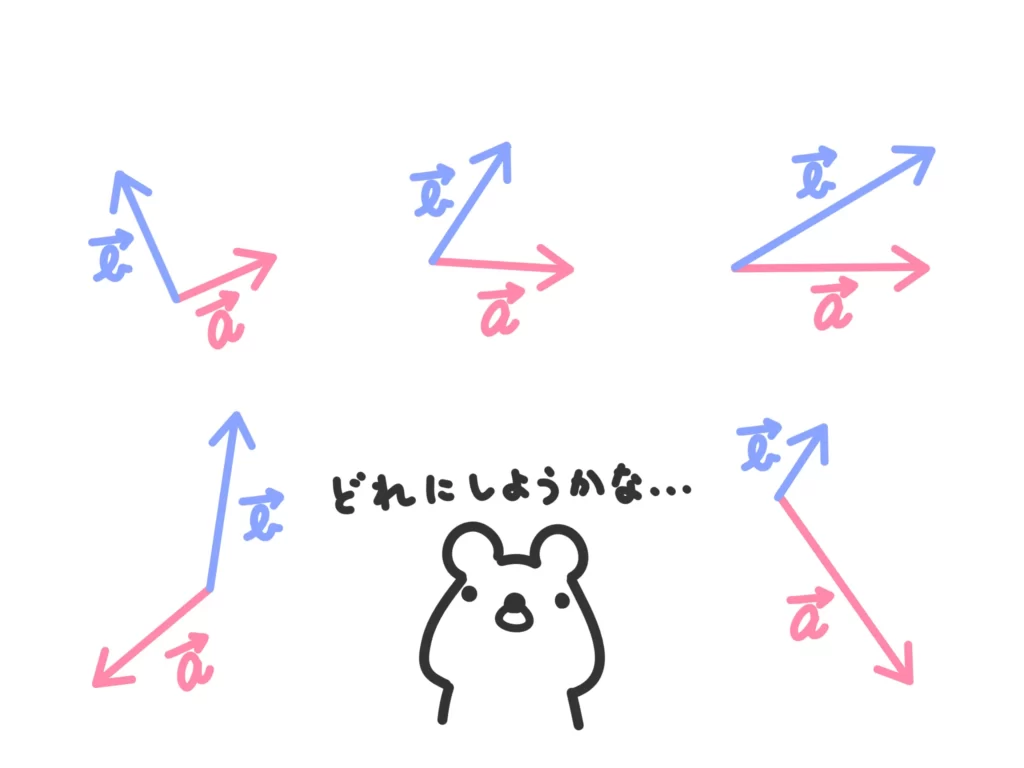
ということで、ベクトルの成分表示です。

もちろん、この質問に関しては、たろう君が言うようになんでもいいんだからなんでもいいです。正解なんかありません。

ただ、常識的な感覚、というか「汎用性が高く」「使いやすい」方向と大きさの２つのベクトルと言われるとどうでしょう…。なんとなく「きちんとした方向と大きさのベクトル２組」を用意したくなりませんか？

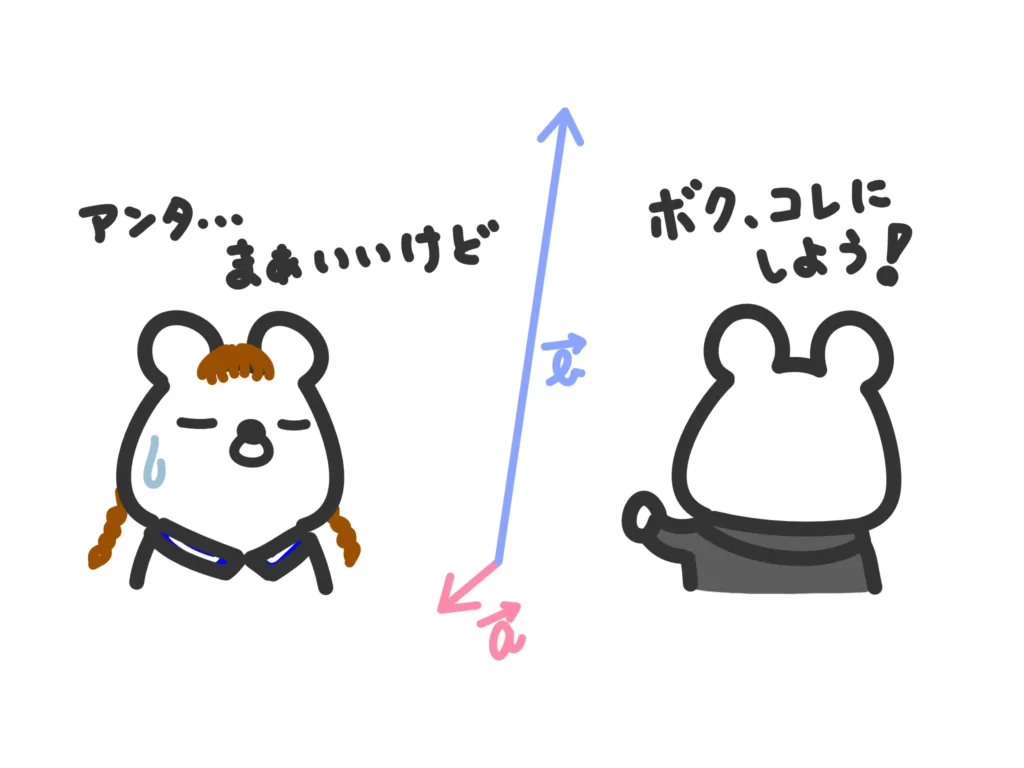
ということで、答えの一つとして「水平右方向と垂直上方向に向いた大きさ１のベクトル」を基底ベクトルとします。

せんせ

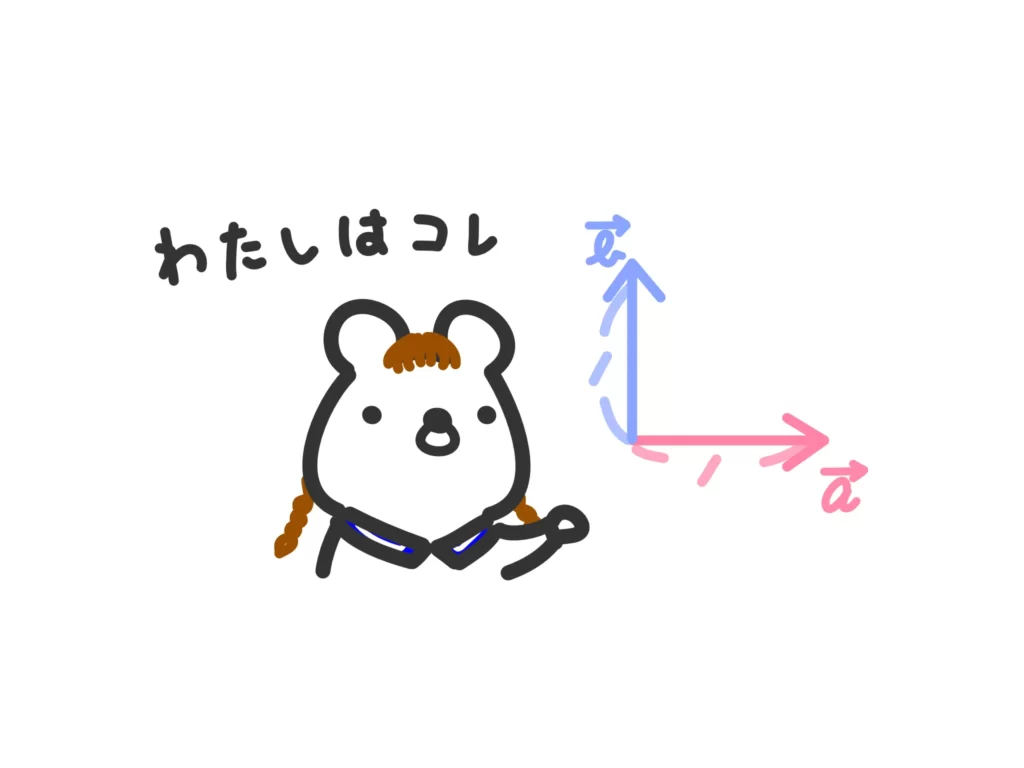
水平、垂直というのがキレイですよね。さらに大きさも１とすることで伸ばしやすくしています。

この２つのベクトルを伸ばして足せば平面上のどんなベクトルでも表すことができるのですが、単純に「横に◯、縦に△進む」と言えばわかりやすいと思います。

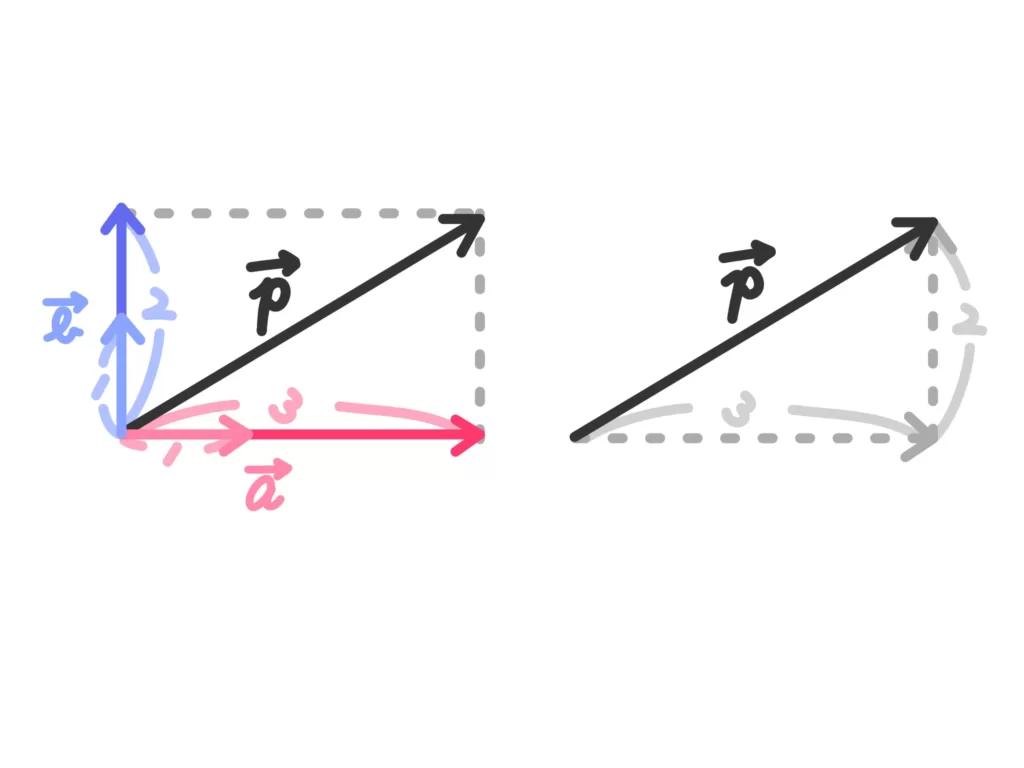
これを水平方向（\(x\)成分）、垂直方向（\(y\)成分）として表したものがベクトルの成分表示です。

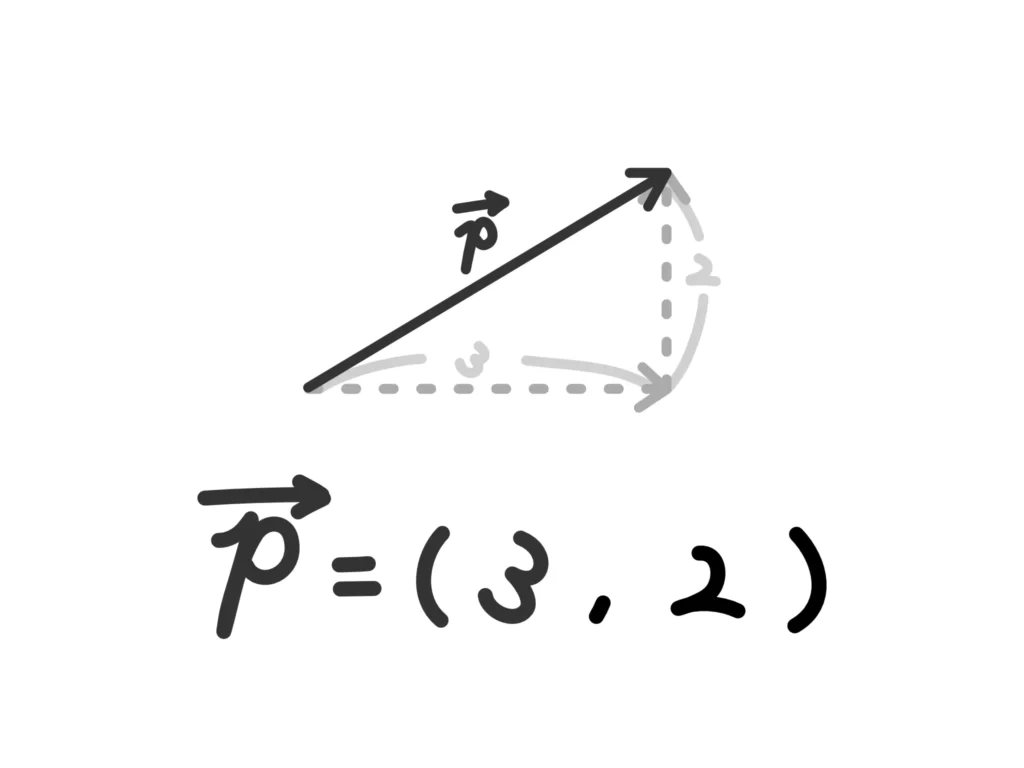
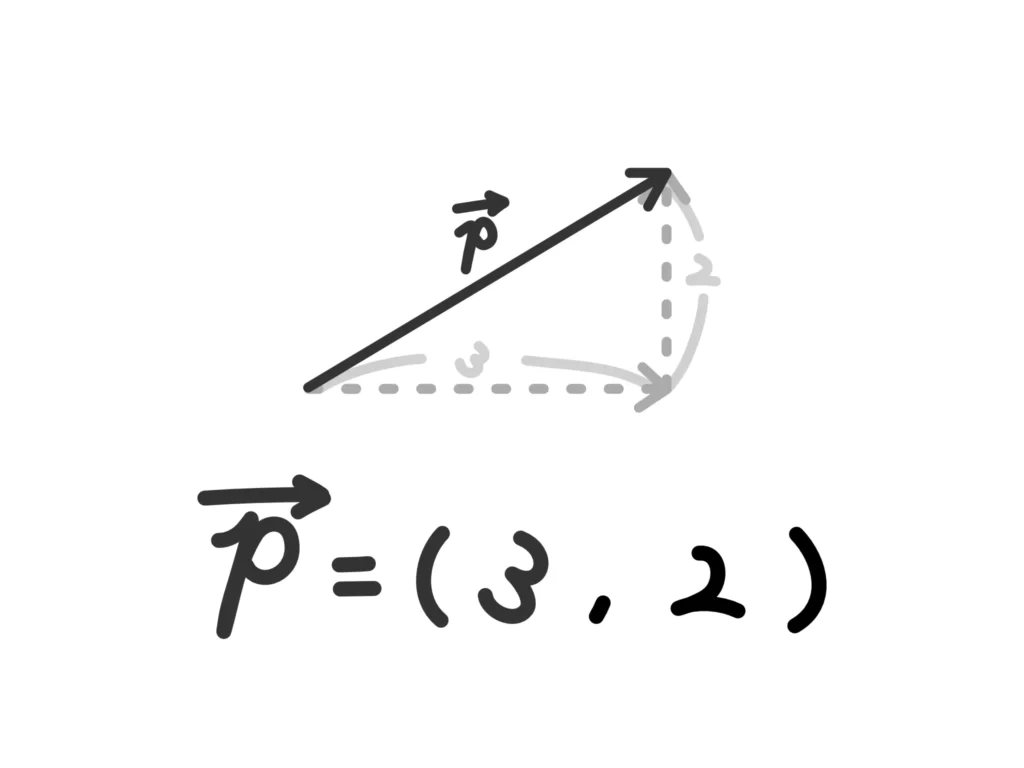
ベクトルの成分表示

水平方向に\(a_1\)、垂直方向に\(a_2\)進んでできるベクトル\(\overrightarrow{a}\)を

\(\overrightarrow{a}=(a_1, a_2)\)

とかく。

これをベクトル\(\overrightarrow{a}\)の成分表示といい、\(a_1\)を\(x\)成分、\(a_2\)を\(y\)成分という。

また、その考え方の性質上「座標平面」との関係が深いです。

せんせ

というか、成分表示と点の座標の表示方法はめちゃくちゃ似てます！…が、これらは基本的に別物です。きちんと区別をつけるようにしましょう。

（点の座標）＝（成分表示）となるのはベクトルの始点が原点のときだけです。

点の座標とベクトルの成分表示の関係

点\(A(a_1 , a_2)\)のとき、

ベクトル\( \overrightarrow{OA} = (a_1 , a_2)\)

また、点\(A(a_1 , a_2)\)、点\(B(b_1 , b_2)\)のとき、

ベクトル\( \overrightarrow{AB} = (b_1-a_1 , b_2-a_2)\)

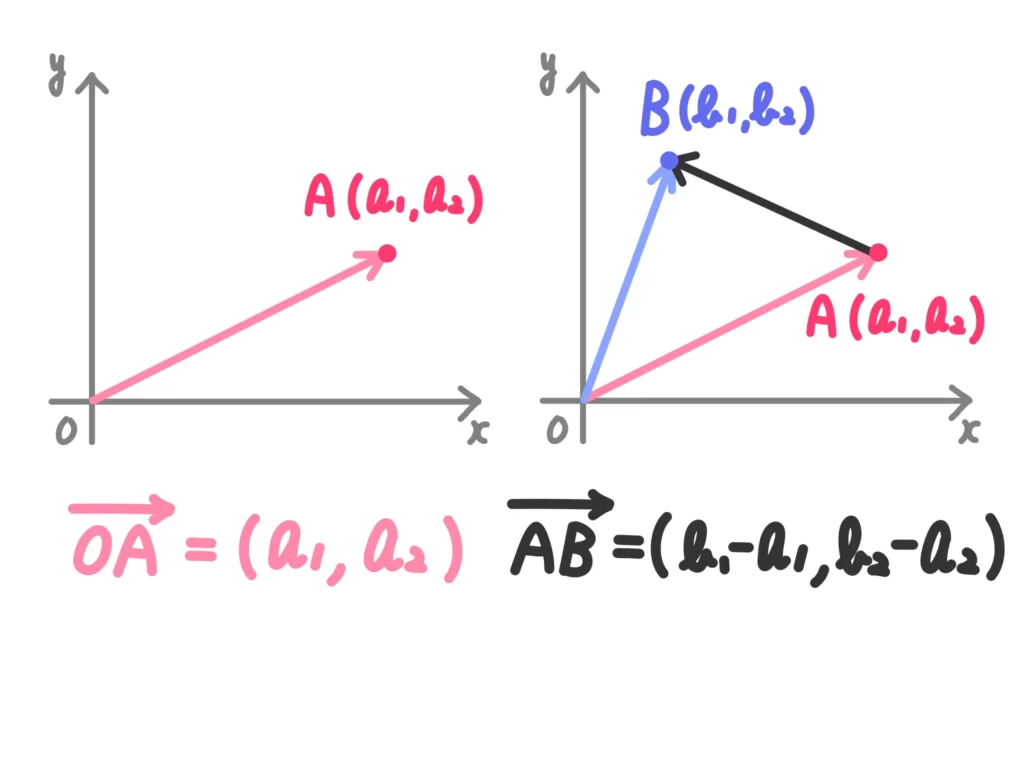
（説明）

\( \overrightarrow{AB}\)について。

始点が原点のときに（点の座標）＝（成分表示）となるので、こちらの記事で説明したように始点を原点に揃えると、

\( \overrightarrow{AB} = \overrightarrow{OB} – \overrightarrow{OA}\)となります。

よって、ベクトル\( \overrightarrow{AB} = (b_1-a_1 , b_2-a_2)\)となります。

せんせ

ベクトルの引き算を使って始点を揃える操作はかなり使います！

ベクトルの大きさを成分計算してみる

これは簡単です！三平方の定理がわかればOK！

成分表示されたベクトルの大きさ

\(\overrightarrow{a} = (a_1 , a_2)\)のとき、

\(|\overrightarrow{a}| = \sqrt{a_1^2 + a_2^2}\)

ベクトルの内積を成分計算してみる

内積の記事で説明しましたが、こちらの成分計算を内積の定義としてもOKです。

成分表示されたベクトルの内積

\(\overrightarrow{a} = (a_1 , a_2)\)、\(\overrightarrow{b} = (b_1 , b_2)\)のとき、

内積\(\overrightarrow{a} \cdot \overrightarrow{b} = a_1 b_1 + a_2 b_2\)

せんせ

「定義」と言ってしまってもいいですが、ベクトルの大きさを利用することで証明も可能です。

（証明）

\(|\overrightarrow{a}-\overrightarrow{b}|^2 = |\overrightarrow{a}|^2-2\overrightarrow{a} \cdot \overrightarrow{b} + |\overrightarrow{b}|^2\)

\((a_1 -b_1)^2 + (a_2-b_2)^2 = a_1^2 + a_2^2 -2\overrightarrow{a} \cdot \overrightarrow{b} + b_1^2 + b_2^2\)

\(a_1^2 -2 a_1 b_1 + b_1^2 + a_2^2 – 2 a_2 b_2 + b_2^2 = a_1^2 + a_2^2 -2\overrightarrow{a} \cdot \overrightarrow{b} + b_1^2 + b_2^2\)

\(-2 a_1 b_1 – 2 a_2 b_2 = -2\overrightarrow{a} \cdot \overrightarrow{b}\)

よって

\(\overrightarrow{a} \cdot \overrightarrow{b} = a_1 b_1 + a_2 b_2\)（終）

まとめ

ベクトルの成分表示は、ベクトルの中でも計算が得意な部分です。

成分表示はゴリゴリと計算する感覚を押さえておきましょう。

せんせ

ベクトルはこのゴリゴリ計算と図形的な考察部分の、バランスと橋渡しが重要です。