母平均の推定とは？【教科書で触れられないポイントまで解説】

2023年9月21日

統計における推定の基本に「母平均の推定」というものがあります。

この記事では高校教科書レベルの母平均の推定について教科書では触れられていない部分も補足しながら説明していきます。

母平均の推定とは？

たろぅ

なるほど…この「５個入りギガジャンボドーナツ」、４００個を調べたけど、重さの平均は203gか。
じゃあまぁ、このメーカーの「５個入りギガジャンボドーナツ」の重さの平均は203gと言ってもいいかな。

はなこ

（200g超えのドーナツ…）
でも、それってぜーんぶのドーナツ調べたわけじゃないから『このメーカーの「５個入りギガジャンボドーナツ」の重さの平均』＝「本当に正しい平均（母平均）」って言ったらまずくない？

たろぅ

確かにそうだけど、でもまぁそれっぽい値にはなるんじゃないの？
「本当に正しい平均」に近い値だとは思うけどな。

はなこ

でも「本当に正しい平均」とは言ったらダメよね？多分その203gってズレがあると思うし…。

たろぅ

じゃあどうやって「本当に正しい平均」を推定するんだよ？そんなこと言ってたら、サンプルから得られた平均じゃあ絶対ズレが生じると思うけど。

ということで母平均の推定です。

教科書ではいきなり正規分布が出てきたり、標準正規分布に変換したり、信頼度95％の信頼区間なんかが出てきて、「よくわかんない」となりがちなところです。

せんせ

まずは、サンプル（標本）から母集団の母平均を推定する際の考え方について説明していきましょう。

題名通り「標本から母集団の母平均を推定する」というのが本題ですが、実ははなこさんとたろうくんのやりとりが元々の発想になります。

大数の法則から、標本の大きさを大きくすれば標本平均は母平均に近づいてきます。

ですが、近づくとはいえ、その標本平均は母平均とズレが生じます。

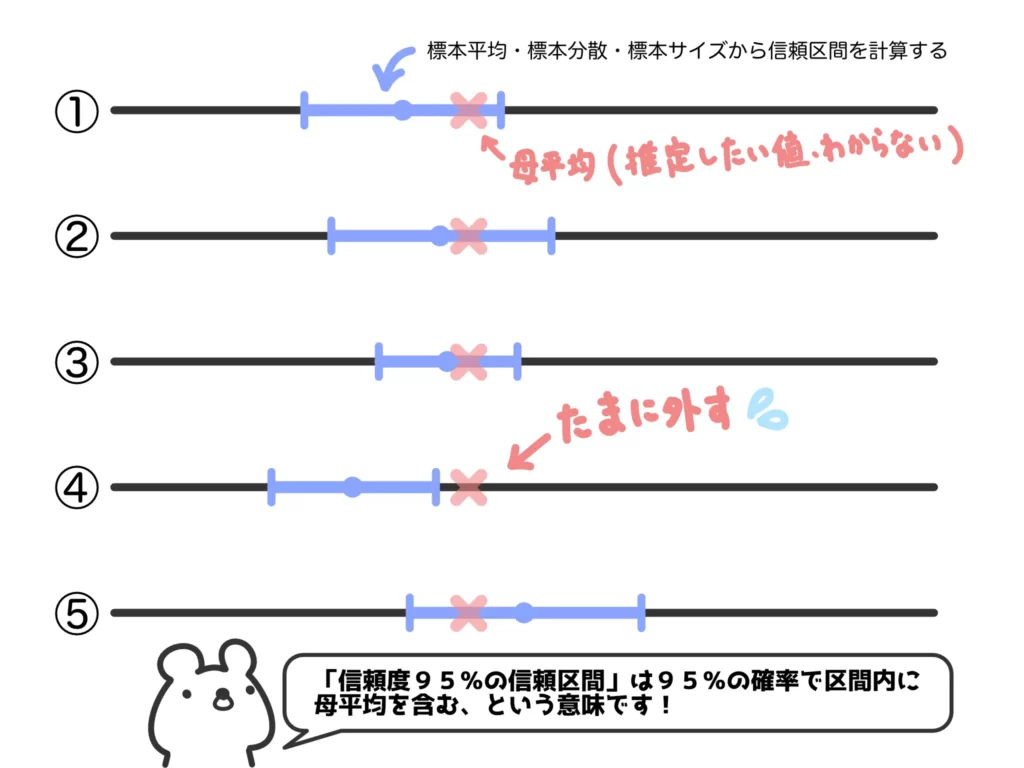
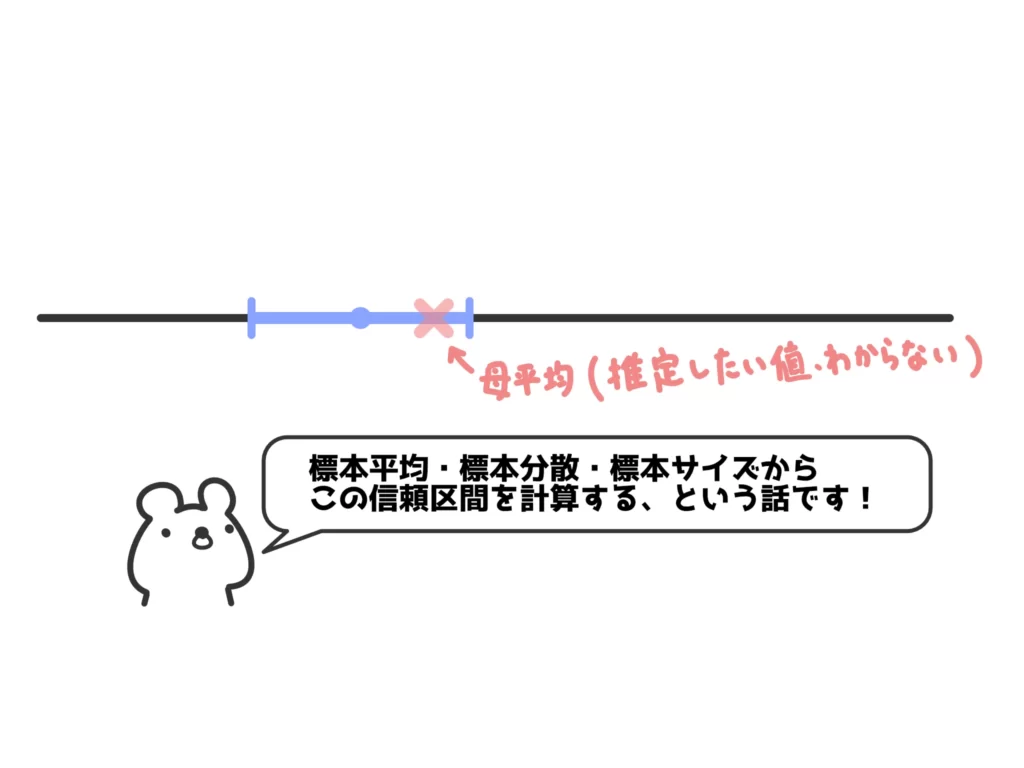
そこで、標本から得られた平均や分散を使って「母平均（たろうくんたちが言う「本当に正しい平均」）の値がこの区間には高確率（例えば９５％とか）で含まれるはずだ！」という区間を計算し、それを使って推定しよう、というのが母平均の区間推定です。

ここでもう一つ重要なポイントがあって、それは「標本の大きさを大きくすれば、標本平均の分布は正規分布に近似できる」という中心極限定理といわれるものです。

せんせ

中心極限定理についてはこちらの記事も合わせて読んでくれると理解が深まると思います！

あわせて読みたい

大数の法則と中心極限定理【わかりやすく雰囲気が伝わるように説明】統計的な推測をする際に、全体（母集団）からサンプルをいくつか取ってきて（標本）、その特徴を調べる、という方法があります。この記事では、標本の特徴を使って母集…

ということで、母平均の推定については以下のような考え方の流れになります。

「母平均を推定したい。ただし、母平均≒標本平均という発想（点推定という）ではなく、標本平均と標本分散を使って母平均が高確率で入る区間を計算して、『この区間に高確率で真の母平均がありますよ』と主張したい（区間推定という）」→

「『標本平均の分布は正規分布に近似できる』という性質を使って、正規分布上で母平均が高確率（普通は95％とか99％）で入る範囲を求めたい」→

「実際の計算は標準正規分布に変数変換して求める」

せんせ

こんな感じですね。
標本から得られたデータから「十中八九この区間に母平均が入るはずだ」と数学的に主張できたら「その標本の平均じゃズレがあるんじゃないの？」というモンクに反論できます。

実際に母平均の区間推定をしてみよう！

要は先ほどの図の区間を求める、という作業をしていきます。

まず、こちらの記事で説明したように、標本平均\(\bar{x}\)の分布は標本の大きさ\(n\)が大きければ、

正規分布\(\displaystyle N\left( \mu, \frac{\sigma^2}{n} \right) \)（ただし、\(\mu\)は母平均、\(\sigma^2\)は母分散とする）

に従う、という性質があります。

正規分布はこのままでは処理しにくいので、標準正規分布に変換しておきます。

標本平均\(\bar{x}\)は、

\(\displaystyle Z=\frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\)（\(\displaystyle \frac{（確率変数）-（平均）}{（標準偏差）}\)）

で標準化することができます。

せんせ

それでは、この確率変数\(Z\)が「95％の確率で母平均を含む」という値の範囲を求めていきましょう。

標準正規分布表を使えば、0.95となる\(Z\)の範囲は、

\(P(|Z| \leq 1.96) = 0.95\)

となります。これを変形していきます。

\(\displaystyle P \left( \left|\frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\right| \leq 1.96 \right) = 0.95\)

\(\displaystyle P \left( |\bar{x}-\mu| \leq 1.96\frac{\sigma}{\sqrt{n}} \right) = 0.95\)

\(\displaystyle P \left( \bar{x}-1.96\frac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{x}+1.96\frac{\sigma}{\sqrt{n}} \right) = 0.95\)

つまり、母平均\(\mu\)が\(\displaystyle \bar{x}-1.96\frac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{x}+1.96\frac{\sigma}{\sqrt{n}}\)に入る確率は0.95になる、という式が得られました。

逆にいうと、0.95つまり９５％の確率で母平均\(\mu\)を含む区間は\(\displaystyle \bar{x}-1.96\frac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{x}+1.96\frac{\sigma}{\sqrt{n}}\)ということがわかります。

信頼度９５％の信頼区間

母平均\(\mu\)の区間推定をしたい。標本をとってきたときの標本の大きさ\(n\)、標本平均\(\bar{x}\)だったとし、母分散\(\sigma^2\)であるとすると、信頼度９５％の信頼区間は

\(\displaystyle \bar{x}-1.96\frac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{x}+1.96\frac{\sigma}{\sqrt{n}}\)

となる。ただし、標本の大きさ\(n\)が大きい場合、標本分散\(s^2\)を母分散\(\sigma^2\)の代わりに使ってもよいので、

\(\displaystyle\bar{x}-1.96\frac{s}{\sqrt{n}} \leq \mu \leq \bar{x}+1.96\frac{s}{\sqrt{n}}\)

と計算できる。

ちなみに、上の例では信頼度９５％の信頼区間でしたが、問題によっては信頼度９０％や９９％の信頼区間を求めないといけないこともあります。

最初の\(P(|Z| \leq 1.96) = 0.95\)の部分が変わる、つまり1.96の部分が９０％なのか？９９％なのか？によって変化します。

ここまでの話で「ん？なんか違和感があるな…」と思う人もいるかもしれません。

恐らくその違和感の正体は、

母平均を推定するために、本来母分散が必要なのに標本分散を使っている、

というところでしょう。多分。

標本平均の標準化の式\(\displaystyle \frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\)の\(\sigma^2\)は正確には母分散の値です。

たろぅ

なんで母分散使わないといけないところを標本分散使っちゃってるんじゃい…。「標本サイズが大きければ標本分散≒母分散として計算してよい」って、それならそもそも母平均≒標本平均でいいじゃないか…。

少なくとも私は最初そう思いました。

後々勉強してわかったのですが、正直言うと、実際には母平均の推定の際に母分散≒標本分散で計算することはありません。

母分散がわからないときには、標本から得られる不偏分散とt分布と言われる分布を使って推定します。

つまり、母分散がわからないときに教科書のように標準正規分布を使って推定することってないんです…。

区間推定の意味を理解して練習をさせるために無理矢理標準正規分布でやってる、という妥協案的な感じで、t分布まで教えない教育課程の事情がうかがえる推定方法ですね。

せんせ

それでは実際に区間推定をしてみましょう！

例１．「５個入りギガジャンボドーナツ」を４００個を調べたところ、重さの平均（標本平均）は203g、分散（標本分散）は2500でした。信頼度９５％の信頼区間を求めなさい。

（解）

信頼度９５％の信頼区間の式を覚えていたらそれに代入するだけです。

\(\bar{x}-1.96\frac{s}{\sqrt{n}} \leq \mu \leq \bar{x}+1.96\frac{s}{\sqrt{n}}\)

の\(\bar{x}=203\)、\(n=400\)、\(s=\sqrt{2500}=50\)を代入します。

\(s\)は分散ではなく、\(\sqrt{分散}\)、つまり標準偏差だということに注意してください。

\(203-1.96\frac{50}{\sqrt{400}} \leq \mu \leq 203+1.96\frac{50}{\sqrt{400}}\)

\(198.1 \leq \mu \leq 207.9\)…（答）

\(\displaystyle P \left( \left|\frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\right| \leq 1.96 \right) \)の式を使ってもよいです。

この後の式変形が面倒な気もしますが、標準化の式\(\displaystyle \frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\)（\(\displaystyle \frac{（確率変数）-（平均）}{（標準偏差）}\)）を押さえられるのと、

\(P(標準化した変数 \leq 標準正規分布から読んだ値)=必要な確率\)

という「必要な確率とそれに対する標準正規分布表から読んだ確率変数の値」の関係を押さえられる、というメリットがあります。

例２．「５個入りギガジャンボドーナツ」を４００個を調べたところ、重さの平均（標本平均）は203g、分散（標本分散）は2500でした。信頼度９９％の信頼区間を求めなさい。

（解）

信頼度９５％の信頼区間を丸暗記して対応していると、こういうときにちょっと困ります。

たろぅ

信頼度９５％のときとなにがどう違うんだぁ…。

できれば、先ほどの

\(\displaystyle P \left( \left|\frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\right| \leq 1.96 \right) =0.95\)

の式を使う方がいいでしょう。

信頼度を９９％にしたければ、

\(\displaystyle P \left( \left|\frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\right| \leq \alpha \right) =0.99\)

となる\(\alpha\)を標準正規分布表から読めばOKです！標準正規分布表はこちらかこちら（上側確率）をご覧ください。

標準正規分布表は半分の確率しか与えられていないので、９９％=0.99の半分、すなわち0.495となる確率変数の値を読みます。

せんせ

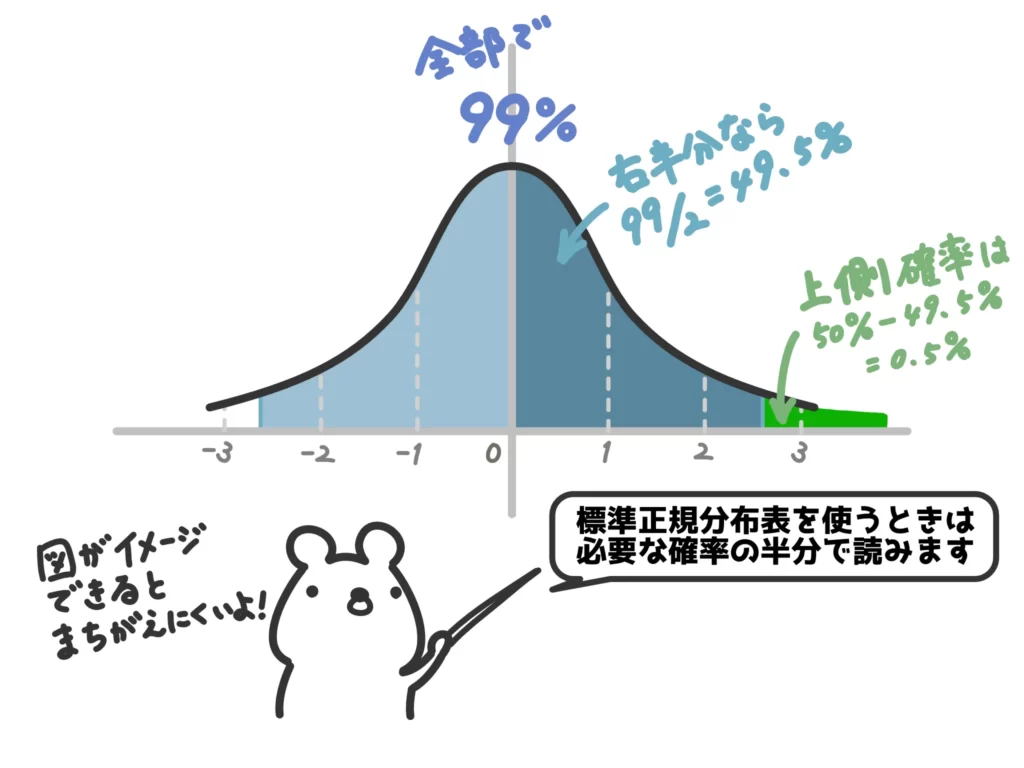
上側確率であれば、１％=0.01の半分なので０.５％=0.005のところですね。

標準正規分布表を使って0.495となる確率変数の値を読むと、2.58となります。

この2.58と\(\bar{x}=203\)、\(n=400\)、\(s=\sqrt{2500}=50\)を代入すると、

\(\displaystyle P \left( \left|\frac{203-\mu}{\frac{50}{\sqrt{400}}}\right| \leq 2.58 \right) =0.99\)

実際には\(\mu\)を含む範囲を求めればよいので、

\(\displaystyle \left|\frac{203-\mu}{\frac{50}{\sqrt{400}}}\right| \leq 2.58\)

の部分を計算すればOKです。

\(\displaystyle |203-\mu| \leq 2.58\frac{50}{\sqrt{400}}\)

\(\displaystyle -2.58\frac{50}{\sqrt{400}} \leq 203-\mu \leq 2.58\frac{50}{\sqrt{400}}\)

\(\displaystyle 203-2.58\frac{50}{\sqrt{400}} \leq \mu \leq 203 + 2.58\frac{50}{\sqrt{400}}\)

\(\displaystyle 196.6 \leq \mu \leq 209.45 \)…（答）

せんせ

① 信頼度９５％のときよりも区間が広くなります。区間が広い方が母平均を含む可能性が高くなる、というのはわかりやすいと思います。
② 似たような問題で「母比率の推定」なんかもありますが、\(\displaystyle \frac{s}{\sqrt{n}}\)が変わります。やはり、そういうときも
\(P(標準化した変数 \leq 標準正規分布から読んだ値)=必要な確率\)
を知っていた方が安心です。信頼度９５％の信頼区間を丸覚えするのはあまり効率がよくありません。
覚えるなら、
「(平均)ー(95%や99%となる確率変数)×(標準偏差)
\(\leq \mu \leq \)
(平均)＋(95%や99%となる確率変数)×(標準偏差)」
という各変数の意味を覚えておきましょう。