「情報」が共通テストに課される！？サンプル問題の解説とねらい③

サンプル問題の解説第３弾です。第３問はデータ分析の問題です。

サンプル問題の解説はこれで一通り終わりですが、結果的にかなり幅広い知識が必要になるテストだな、という感想です。

少しずつでもよいので、対策していきましょう。

第１問、第２問の解説はこちら。

オリジナルの問題を確認したい、という人はこちらからどうぞ。（外部リンクです）

第３問（問１）

ア〜ウの解説

S高等学校サッカー部のマネージャーをしている鈴木さんは，「強いサッカーチームと弱いサッカーチームの違いはどこにあるのか」というなかなかアグレッシブなテーマで研究している、という話から、

ワールドカップ出場３２チームを決勝進出１６チーム、予選敗退１６チームに分け、様々なデータを集めて以下の図を作りました。

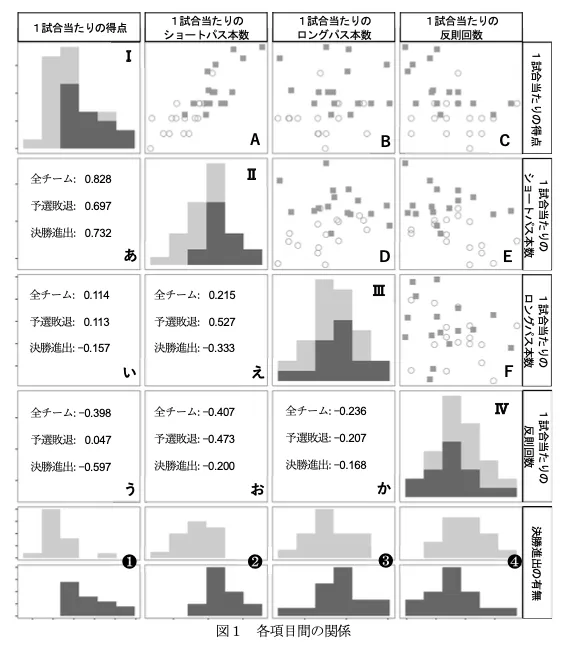
1を見ると，予選敗退チームにおいてはほとんど相関がないが，決勝進出チームについて負の相関がある項目の組合せは，1試合当たりの （ ア ） と （ イ ） である。また，決勝進出チームと予選敗退チームとで，相関係数の符号が逆符号であり，その差が最も大きくな っている関係を表している散布図は（ ウ ）である。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

ア、イについては、問題文をそのまま読んでいただければ大丈夫です。

相関係数とは、２つのデータの間に関係があるかないか、を示します。相関係数を\(r\)とすると、\(-1 \leq r \leq 1\)の間の数値をとり、1に近ければ正の相関（一方のデータが増えれば（減れば）もう一方も増える（減る））があり、−１に近ければ負の相関（一方のデータが増えれば（減れば）もう一方が逆に減る（増える））があり、０に近ければ２つのデータに関係がない、ということになります。

ア、イの答えは、問題の条件に合致する組み合わせを読み取って、０.得点、3．反則回数です。

ウはちょっとわかりにくいですが、散布図に起こすと、右肩上がりが正の相関、右肩下がりが負の相関になります。

ということでAは丸も四角も右肩上がりなので違います、Bはどちらも散っているように見えます、E、Fは丸も四角も若干右肩下がりに見えます、Cは丸が散っているかわずかに右肩下がりで四角が右肩下がりになって見えます、Dは丸が右肩上がり、四角が右肩下がりに見えます。

ということで、ウの答えは③Dです。

エの解説

０．それぞれの散布図の中で，決勝進出チームは黒い四角形(■)，予選敗退チームは白い円(○)で表されている。

１．全参加チームを対象としてみたとき，最も強い相関がある項目の組合せは1試合あたりの得点と1試合あたりのショートパス本数である。

２．全参加チームについて正の相関がある項目の組合せの中には，決勝進出チーム，予選敗退チームのいずれも負の相関となっているものがある。

３．1試合当たりのショートパス本数の分布を表すグラフ❷で，下の段は決勝進出チームのヒストグラムである。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

この中から誤っているものは②全参加チームについて正の相関がある項目の組合せの中には，決勝進出チーム，予選 敗退チームのいずれも負の相関となっているものがある。です。そのような組み合わせはありません。

第３問（問２）

オ〜ケの解説

結局「得点」と「ショートパス」について着目した鈴木さん。決勝進出チームと予選敗退チームに分けてデータを取り出し、回帰直線をかきました。

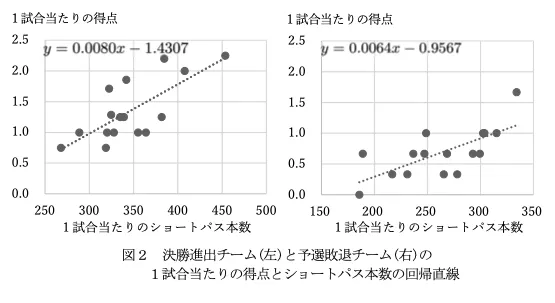
鈴木さんは，この結果からショートパス 100 本につき，1試合当たりの得点増加数を決勝進出チームと予選敗退チームで比べた場合，0. （オカ）点の差があり，ショートパスの数に対する得点の増加量は決勝進出チームの方が大きいと考えた。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

オ、カについてですが、決勝進出チームと予選敗退チームの回帰曲線が、

• 決勝進出チーム → \(y=0.0080x-1.4307\)
• 予選敗退チーム → \(y=0.0064x-0.9567\)

となっています。例えば、これに先ほど先生が言った\(x=100\)を代入したら、決勝進出チームは-0.6307、予選敗退チームは-0.3167になり、１試合あたりの得点がマイナスの値になってしまいますが、そこはハッキリ言ってどうでもいいところです。

ポイントは「ショートパス１００本につきどの程度得点が増加するか？」ですが、

０本→１００本、２００本→３００本、１０００本→１１００本、…

のどこを考えても直線なので増加数は同じ、というところです。（ここでは具体的には値を書きませんが、気になる人は試しに代入してどれだけ得点が増えたか、を調べてみてください。）

ここからは数学の話になりますが、直線の式では、

増加率＝直線の傾き

でした。

つまり、具体的な値を全て計算する必要はなく、（それぞれの定数部分、-1.4307と-0.9567は増加数とは関係ない。関係あるのは【傾き】×\(x\)の部分だけ。）

決勝進出チームは

\(0.0080x\)の部分にだけ\(x=100\)（と、正確には\(x=0\)）を代入 → 0.80

予選敗退チームは

\(0.0064x\)の部分にだけ\(x=100\)（と、正確には\(x=0\)）を代入 → 0.64

を求めれば、１００本につき、の得点増加数がわかります。よって、その差オカは0.80-0.64=0.16です。

また，1試合当たりのショートパスが 320 本のとき，回帰直線から予測できる得点の差は，決勝進出チームと予選敗退チームで，小数第3位を四捨五入して計算すると， 0.0（ キ ）点の差があることが分かった。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

キは\(x=320\)を代入して頑張って計算するしかありません。

決勝進出チームは\(y=0.0080 \times 320 -1.4307=1.1293\)

予選敗退チームは\(y=0.0064 \times 320 -0.9567=1.0913\)

なので、その差は1.1293-1.0913=0.038。小数第３位を四捨五入するので、キは0.04となります。

さらに，ある決勝進出チームは，1試合当たりのショートパス本数が 384.2 本で，1試合当たりの得点が 2.20 点であったが，実際の1試合当たりの得点と回帰直線による予測値との差は，小数第3位を四捨五入した値で0. （クケ）点であった。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

クケも問題から読み取ると、\(x=384.2\)を決勝進出チームの回帰直線\(y=0.0080x-1.4307\)に代入して頑張って計算するしかないのがわかると思います。

\(y=0.0080 \times 384.2 -1.4307=1.6429\)

という回帰直線からの予測値が出るので、その差は2.20-1.6429=0.5571。小数第３位を四捨五入するので、クケは0.56となります。

第３問（問３）

コサは、以下の図からの「読み取り→正しいもの」を選ぶ問題です。

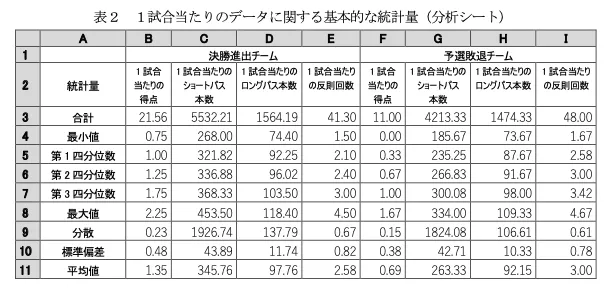
０．1試合当たりのロングパス本数のデータの散らばりを四分位範囲の視点で見ると， 決勝進出チームよりも予選敗退チームの方が小さい。
１．1試合当たりのショートパス本数は，決勝進出チームと予選敗退チームともに中央値より平均値の方が小さい。
２．1試合当たりのショートパス本数を見ると，決勝進出チームの第1四分位数は予選敗退チームの中央値より小さい。
３．1試合当たりの反則回数の標準偏差を比べると，決勝進出チームの方が予選敗退チームよりも散らばりが大きい。
４．1試合当たりの反則回数の予選敗退チームの第1四分位数は，決勝進出チームの中央値より小さい。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

このへんの四分位数の話は高校数学Iのデータの分析分野で勉強しますが、ここでとりあえず必要な知識は

第２四分位数＝中央値

というものです。

それを踏まえてもう一度表を確認すると、解答群の赤のマーカー部分が間違いだ、ということがわかるはずです。

よってコサの答えは０と３です。

第３問（問４）

シ〜ソの解説

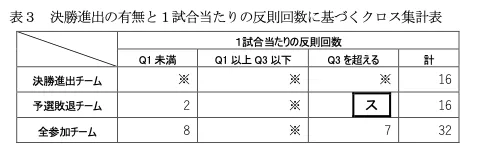
鈴木さんは，作成した図1と表2の両方から，（ シ ）ことに気づき，決勝進出の有無と1試合当たりの反則回数の関係に着目した。そこで，全参加チームにおける1試合当たり の反則回数の第1四分位数(Q1)未満のもの，第3四分位数(Q3)を超えるもの，Q1 以上 Q3 以下の範囲のものの三つに分け，それと決勝進出の有無で，次の表3のクロス集計表に 全参加チームを分類した。ただし，※の箇所は値を隠してある。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

（ シ ）の解答群
０．1試合当たりの反則回数が最も多いチームは，決勝進出チームである

１．1試合当たりの反則回数と1試合当たりの得点の間には，全参加チームにおいて正の相関がある

２．1試合当たりの反則回数と1試合当たりの得点の間には，決勝進出チームと予選敗退チームのそれぞれで負の相関がある

３．図1の❹のヒストグラムでは決勝進出チームの方が予選敗退チームより分布が左にずれている

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

シの解説です。０．は表２を見れば違う、というのがわかります。

それ以下は、実は鈴木さんが作った表３は四分位数の表なので「相関」はまったく関係ないことから、「答えは３だろうな」というおおよその予想は立ちます。（ヒストグラムは「散らばり」が見える、四分位数は「散らばり」を数値化しているので関係がある。）

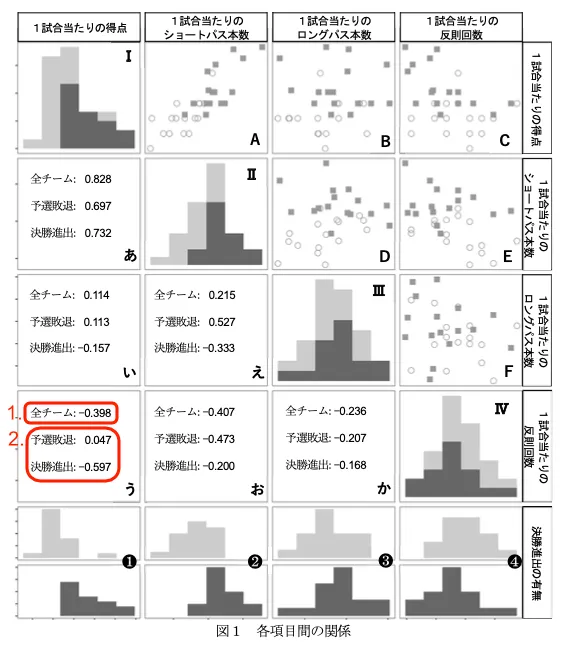
ということで、やはりシの答えは３です。

スについては、ちょっと意味が分かりづらいですね…。最初「どこ見て確認するんだ？」と思ってしまいました。問題はその次までよく読みましょう…。

表３と次の文章で確認していきます。

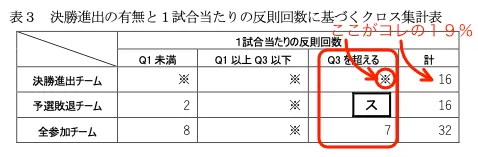
この表から，決勝進出チームと予選敗退チームの傾向が異なることに気づいた鈴木さんは，割合に着目してみようと考えた。決勝進出チームのうち1試合当たりの反則回数が全参加チームにおける第3四分位数を超えるチームの割合は約19%であった。また，1試合 当たりの反則回数がその第1四分位数より小さいチームの中で決勝進出したチームの割合は（ セソ ）%であった。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

「決勝進出チームのうち」、1試合当たりの反則回数が「全参加チームにおける第3四分位数を超える」チームの割合は約19%であった。

「決勝進出チームのうち」→ 決勝進出の１６チーム。「全参加チームにおける第3四分位数を超える」→ Q3を超える。

です。この割合が１９％、ということですね。つまり、

（決勝進出チームでQ3を超えるチーム数）÷１６＝大体0.19

ということなので、計算すると（決勝進出チームでQ3を超えるチーム数）=3.04、つまり３チームだとわかります。

よって、表３の「Q３を超える」列を縦で見ると、予選敗退チームのこの列の数は７−３＝４となり、スは４です。

スの流れを理解できれば最後はわかりやすいかな、と思います。

セソは、表３の「Q１未満」列の決勝進出チームの割合を出したいので、

決勝進出チーム数のこの列の数は８−２＝６ですから、

６÷８＝0.75、つまりセソは75％となります。

まとめ

最後は数学的要素も入ってきました。数学の「データの分析」分野の問題と比べれば数学的な難易度は低いです。

が、「回帰直線の意味」や「四分位数の意味」を、数学の式的な意味を実用的なレベルに落とし込んでおかないと、解答するのは意外と難しいと思います。