「情報」が共通テストに課される！？サンプル問題の解説とねらい②

２０２５年度大学入学共通テストから「情報」が課されることになりました。デジタルデータの基本的な知識、ネットワークの基本的な知識、情報モラルやプログラミング、データ処理まで出題範囲になっています。

はっきり言って、結構大変だと思います。

先生が教えるのが、というよりも生徒が情報リテラシーを高校の３年間のみで身につけるのはかなり厳しい、と思います。

ただでさえやることが多い受験生がここまでの勉強をするとなると、ある程度低学年（高校１、２年。あるいは小学校、中学校からプログラミングは「教養」としてやるべきなのでは？とさえ思います。）からプログラミングに触れておくべきです。今の感覚で言うと、「ピアノ」「水泳」「英語」「プログラミング」みたいな習い事として学ぶべきかと思います。

話が逸れましたが、効率的に学んでいくことが重要だと思うので、大学入試センターが示している情報のサンプル問題の解説をしていきます。

前回の解説はこちら。

あわせて読みたい

「情報」が共通テストに課される！？サンプル問題の解説とねらい① 最近、高校教育業界で話題になっていることがあります。それは2025年度（令和7年度）共通テストで「情報」が課される、という内容です。 令和4年度高校入学生から新たに…

今回はいよいよ目玉となる「プログラミング」の解説です。

解説を先にしますが、情報のプログラミング分野を学ぶ際に重要なポイントも最後に書いておきます。

第２問（問１）

せんせ

いよいよプログラミングの範囲になります。特定の言語、という訳ではなく、プログラミングの思考を問う問題になっています。

たろぅ

えー…。PythonとかJavaとか特定の言語じゃないの？

せんせ

確かに、プログラミングには言語的な特徴やそれぞれの書き方、というのはあるんだけれど、ベースとなる考え方には共通な部分も多いんだよ。その共通な考え方を引っ張り出して問題にしている感じですね。

ということで、早速解説していきましょう！

オリジナルの問題を確認したい、という人はこちらからどうぞ。（外部リンクです）

ア〜ウの解説

まず、１８歳になって選挙権が得られた、というくだりから、比例代表選挙の各党に配分する議席数を決めるプログラミングを組む、という流れで、実際の得票数を表で示した。

後、

Kさん : 今回の議席数は6人だったね。…（中略）…各政党の得票数が何議席分に相当するかは，各政党の得票数をこの基準得票数で割れば求められるね。

Mさん : その考え方に沿って政党ごとの当選者数を計算するプログラムを書いてみよう。ま ず，プログラムの中で扱うデータを図1と図2にまとめてみたよ。配列 Tomei には 各政党の党名を，配列 Tokuhyo には各政党の得票数を格納することにしよう。政党の数は4つなので，各配列の添字は 0 から 3 だね。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

図1、図2は次の通りです。

で、実際のプログラミングを示しながら、

(01)Tomei = [“A 党”,”B 党”,”C 党”,”D 党”]

(02)Tokuhyo = [1200,660,1440,180]

(03)sousuu = 0

(04)giseki = 6

(05) m を 0 から（ ア ）まで 1 ずつ増やしながら繰り返す:

(06)⎿ sousuu = sousuu + Tokuhyo[m]

(07)kizyunsuu = sousuu / giseki

(08) 表示する(“基準得票数:”,kizyunsuu )

(09) 表示する(“比例配分”)

(10) m を 0 から ア まで 1 ずつ増やしながら繰り返す:

(11)⎿ 表示する(Tomei[m],”:”, （イ ）/（ ウ ）)

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

このプログラミングの画面出力が次の通りです。これは(08)、(09)、(11)の「表示する(〜)」の結果です。

Kさん : 得票数に比例して配分すると小数点のある人数になってしまうね。小数点以下の数はどう考えようか。例えば，A党は 2.068966 だから2人が当選するのかな。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

という話に続きます。

解説の前に、「配列？」という人はこちらの記事を読んでみてください！

あわせて読みたい

【教育Python入門】変数の基本とメモリ参照などちょっと詳しい話 2022年度から高校で本格的に始まる「情報I」。2025年度から共通テストでも情報が科目として課されます。 この「教育Python入門」は、プログラミングを教える人にも、学…

せんせ

それでは解説していきます。

まず、以下の点について「読み取り」と「知識」が必要です。

• 議席数６を得票数によって各党に割りたい。つまり「得票数の割合によって分配する」ので「票数を全足したもの」が必要だ。
• プログラミングの配列は「繰り返し」で処理することが多く、そのときに変数（今回はm）に１足しながら実際の計算等をしていく。

これを踏まえると、アは「配列Tokuhyouにあるすべての票数を足す」という処理をしたい、ということになります。

よって、sousuu（「総数」ですね）に配列Tokuhyouの要素を順に足している、というのが(06)の計算です。

せんせ

ちなみにプログラミングの「＝」は「代入する」の意味です。実際の計算を見てみましょう。

sousuu + Tokuhyou[0]（0+1200） を sousuu に代入（sousuuは1200になる）

→ sousuu + Tokuhyou[1]（1200+660） を sousuu に代入（sousuuは1860になる）

→ sousuu + Tokuhyou[2]（1860+1440） を sousuu に代入（sousuuは3300になる）

→ sousuu + Tokuhyou[3]（3300+180） を sousuu に代入（sousuuは3480になる）

ということで、アは③の３になります。

続いてイ、ウについてです。

表示結果とその後に続く会話から、（イ）/（ウ）の計算で「各党にどれくらいの議席が割り振られるか」を求めていることがわかります。

その前にkizyunsuu（基準数）= sousuu（総数） / giseki（議席）を計算し「基準得票数：kizyunsuu（=580）」と表示されているので、このkizyunsuuは１議席を得るために必要な得票数だ、と考えられます。

つまり、「各党にどれくらいの議席が割り振られるか」は（その政党の得票数=配列Tokuhyouに入ってる）/（基準得票数）で計算できます。

よって（イ）/（ウ）は⑧Tokuhyou[m] / b.kizyunsuuとなります。

せんせ

割合が何を意味するのか、という感覚も重要になります。

第２問（問２）

エ〜スの解説

問１の方法では、小数点以下の数値の扱いで上手く議席を割り振ることができませんでした。

Mさん : 先生，比例代表選挙では各政党の当選者数はどうやって決まるのですか? 当選者数が整数なので，割合だけだと上手くいかなかったのです。

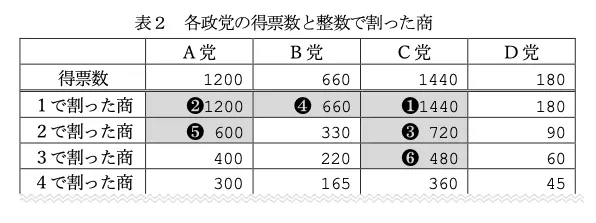
先 生 : 様々な方法があるけど，日本では各政党の得票数を1，2，3，…と整数で割った 商の大きい順に定められた議席を配分していく方法を採用しているよ。この例だと表 2のように，❶から❻の順に議席が各政党に割り当てられるんだ。C党が❶の議席を取っているけど，このとき，何の数値を比較したか分かるかな。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

ポイント
この後の話で、A党〜D党の得票数をA、B、C、Dと書くと、
１．まず得票数が一番多いC党（C）が１議席とる → 得票数÷２した数を計算しておく。（C/2とこのサイトでは書く）
２．「A、B、C/2、D」を比較して一番大きいAが１議席とる → A/2を計算。
３．「A/2、B、C/2、D」を比較して一番大きいC/2が１議席とる → C/3を計算。
４．以下、議席をとったら割る数を増やしていき、その数と他の党の比較をする、を繰り返す。
（この部分のプログラミングコード解説はこちら）

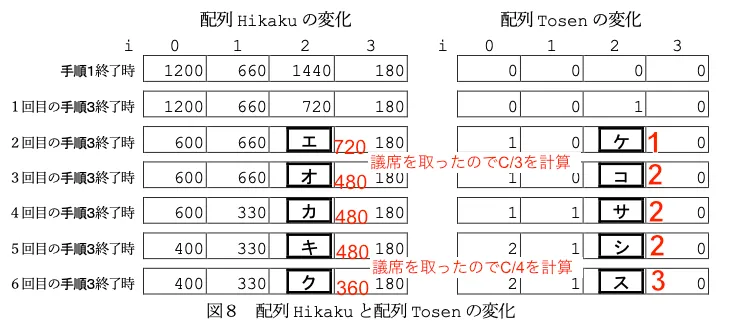
Kさん : 各政党に割り当てる議席を決めるために，比較する数値を格納する配列 Hikaku がいるね。

Mさん : 各政党に配分する議席数(当選者数)を格納する配列 Tosen も必要だね。最初は議席の配分が行われていないから，初期値は全部 0 にしておくね。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

Kさん:「2で割った商」の「2」のように，各政党の得票数を割るときに使う数字はどうすればいいかな。

Mさん:その政党の当選者数+1でいいよね。配列 Tosen が使えるね。そうだ，変化したところだけ計算し直せばいいんじゃない? 議席を配分する手順を書いてみよう。

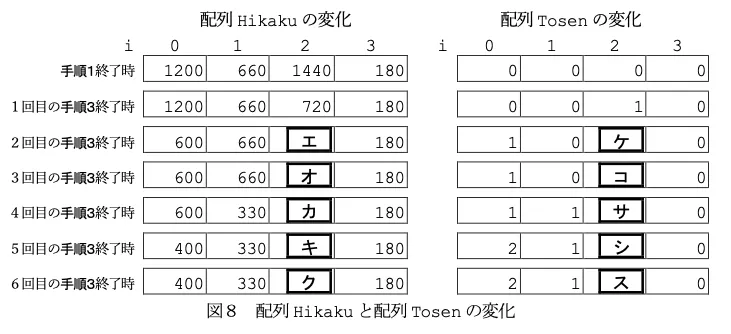
手順1 配列Tokuhyoの各要素の値を配列Hikakuの初期値として格納する。
手順2 配列Hikakuの要素の中で最大の値を調べ，その添字maxiに対応する配列Tosen[maxi]に 1 を加える。
手順3 Tokuhyo[maxi]をTosen[maxi]+1で割った商をHikaku[maxi]に格納する。
手順4 手順2と手順3を当選者数の合計が議席数の6になるまで繰り返す。
手順5 各政党の党名(配列Tomei)とその当選者数(配列Tosen)を順に表示する。

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

ここはあまりプログラミング的な要素はないです。問題文途中のポイントの手順で議席を獲得する、というのと「配列Hikakuは実際に比較する議席数（ポイントで言うところのA、B、C/2、など）を格納、配列Tosenは獲得議席数を意味する」という点が読み取れればOKです。

ということで、エ〜クはC党の比較すべき票数が入ります。エはb.720。これでC党が取るのでオはC/3=⑨480。次はB党がとるのでC党はそのままで、カは⑨480。次はA党がとるのでC党はそのままで、キは⑨480。次はC党が取るので、クはC/4=⑦360。

それに伴い、ケ〜スはC党の獲得議席数が入ります。よって、ケは①１、コは②２、サも②２、シも②２、スは③３となります。

第２問（問３）

ここは、条件と繰り返しを駆使しながら先ほどの問２のプログラミングを実際に組む、という話になります。

せんせ

ここは実際にプログラミングを組んだことがあればイメージしやすい話になります。が、「プログラミングなんか組んだことない！」という人にもわかりやすく説明します。

セ〜チの解説

問題文では色々と話をしていますが、ここでは早速プログラミングコードを見ていきましょう。

(01) Tomei = [“A 党”,”B 党”,”C 党”,”D 党”]

(02)Tokuhyo = [1200,660,1440,180]

(03)Tosen = [0,0,0,0]

(04)tosenkei = 0

(05)giseki = 6

(06)m を0 から ア まで1ずつ増やしながら繰り返す:

(07)⎿ Hikaku[m] = Tokuhyo[m]

(08) （セ） < giseki の間繰り返す:

(09) | max = 0

(10) | i を 0 から ア まで 1 ずつ増やしながら繰り返す:

(11) | | もし max < Hikaku[i]ならば:

(12) | | | （ソ）

(13) | ⎿ ⎿ maxi=i

(14) | Tosen[maxi] = Tosen[maxi] + 1

(15) | tosenkei = tosenkei + 1

(16) ⎿ Hikaku[maxi] = 切り捨て( （タ） / （チ） )

(17)k を0 から ア まで1ずつ増やしながら繰り返す:

(18)⎿ 表示する(Tomei[k],”:”,Tosen[k],”名”)

平成 30 年告示高等学校学習指導要領に対応した 令和7年度大学入学共通テストからの出題教科・科目

まず当然ですが、問２の操作をプログラミングで実行したい、というのは念頭に置いておいてください。

ということで、セについては「（セ）< giseki（議席数）の間繰り返す」なので「（セ）が議席数を満たすまで処理したい」ということがわかります。つまり、セは各政党にそれまで割り振られている議席の合計数が欲しいので、②tosenkei（当選計）となります。

せんせ

プログラミングを読み取るとき、なにがしたいかを言葉に出してみるのは大事です。

そして、「議席数を満たすまで繰り返し処理」に入っていきますが、ここからは少しプログラミング的な感覚が必要です。

まず、「議席数を満たすまで繰り返し処理」をしたいので、ここでは、先ほどのポイントの部分の処理がくることがわかります。一番メインの処理ですね。

ソについて、(11)〜(13)は「 i を増やしながら、もし max < Hikaku[i] ならば （ソ）して maxi に i を代入」という意味です。

せんせ

もう少し噛み砕いてみましょう。

式を使わずに表現すると「配列Hikaku（比較）にある要素を一つ一つ調べて、もし max よりもHikakuの i 番目が大きければ（ソ）して、maxi に i を代入する」という意味になります。

そろそろわかってきたでしょうか？

つまり、（ソ）は「配列Hikakuの要素のうち、最大のものを変数に代入してストックしておく」という操作になります。（ちなみにmaxi に i を代入する、というのも「最大となる要素は i 番目で、その i を maxi に代入してストックしておくよ」という操作です。この辺がプログラミング的ですね）

max（最大値）という意味も考慮すると、ソはmaxという変数にHikaku[i]を代入してストックする、②max = Hiakaku[i]となります。

せんせ

（ソ）が第２問の山場でしたね。

タ、チは微妙に不親切な問題な気がします…（あとで理由を述べます）。

意味としてはHikaku[maxi] = 切り捨て( （タ） / （チ） ) なので、先ほどのmaxiの意味を考えると「配列Hikakuの最大値のところに『切り捨て( （タ） / （チ） )』を代入する、という操作がきます。

ということで『切り捨て( （タ） / （チ） )』は「他の政党と比較して得票数が最大だったから、その政党の比較すべき得票数をnで割るというnを１増やす」という、ポイントでいうところの４の操作がきます。

『切り捨て( （タ） / （チ） )』は、「元の得票数を（獲得議席＋１）で割りたい」という操作になるので、タは元の得票数③Tokuhyou[maxi]（最大となるi番目の得票数）、チは⑧Tosen[maxi]+1（最大となるi番目の議席数＋１）となります。

せんせ

タは⑦と間違えないでくださいね。⑦は配列Toksen（各党に割り振られた議席数）の「最大となる党+1番目（つまり、最大となる党の隣の党、の意味）」になります。

（補足）
先ほどの「タ、チは微妙に不親切」と言ったのは、関数『切り捨て』の定義が全くないからです。
プログラマーからすると、プログラミングの関数は「値を渡せば、決まった処理をしてくれてその結果を返す」という感覚で、関数は自分でコードを書いて定義するか、あらかじめ用意されていたものインポート（要は外注ですが普通は「ここから外注したよ」と宣言する）するか、です。重要なのは「関数は定義や宣言がないと使えないもの」という感覚がある、ということです。Mさんは「『切り捨て』という関数を使ったよ」と言っていますし、『切り捨て』関数がどのような関数かは一般常識的に想像がつくのでギリギリセーフですが、プログラミングをする人からすると微妙に不親切な感じは拭えません。

…まぁ、わかりますよ。こういう感じで特定のプログラミング言語を使わずに関数の話をしようとすると、こういう表現になりますけど…。でも「『切り捨て』関数はどこにあるんだ！」って探しちゃいましたよ。補足、というより愚痴でした、スイマセン。

ツ、テの解説

第２問の最後の問題ツ、テは「議席は割り振るけど、そもそも候補者（その議席に座る人）がいなかったらどうすんの？」という問題です。

条件分岐ではよくやる手法ですが「この条件だけではなく、この条件も、どちらも満たした場合」というやつですね。

(11)を修正したいので「『比較すべき票数が最大なので議席が割り振られた』かつ、『候補者がその議席以上いたら（議席を割り振ってもいいよね）』」としたいです。

ということで、ツは0.and（かつ）、テは0.Koho[i] >= Tosen[i] + 1（Tosen[i]は割り振られた議席だが、②Koho[i] >= Tosen[i] との違いは「獲得している議席」ではなく「獲得議席にさらに１加えようとしたとき」の比較なので。）となります。

プログラミング分野対策の学習法

一通りプログラミング分野の解説をしましたが、ここでは情報のプログラミング分野で重要な学習法の説明をしていきます。

さて、今回のプログラミング分野の解説をして感じたのは、プログラミングの基本である考え方をしっかり学習すべきである、ということです。

Pythonベースでのプログラミングの学習方法についてはこちらから随時更新していきます！

せんせ

ぜひ、チェックをしてみてください！

あわせて読みたい

【教育Python入門】Pythonのプログラミングができる環境を作ろう！ 2025年度大学入学共通テストから「情報」が課されることになりました。 しかもその内容にプログラミングが入ってきます。 さて、先生方、プログラミングを教える準備は…

ここでは簡単に重要になってくるであろう、３つの勉強するべき事柄をあげておきます。

１．配列
２．繰り返し処理（実際のプログラミングで言うところのfor文）
３．条件分岐（実際のプログラミングで言うところのif文）

せんせ

確かに、言語によって様々な特徴はありますし、書き方が違う、という部分もありますが、上記の３点に関しては「プログラミング的」かつ「共通した考え方」なので、最優先で押さえておくべきです。

ということで、この３つのポイントについて解説していきたいと思います。

配列とは

配列とは、いくつかの要素を１セットにしたものです。状況によって、セットにするものは色々と変わります。今回で言えば「政党」「得票数」「候補者の数」は１セットにしておいた方が扱いやすいです。

例えば、

Tomei = [“A 党”,”B 党”,”C 党”,”D 党”]、Tokuhyo = [1200,660,1440,180]という配列を準備したとき、

「各配列の０番目（A党の情報が欲しい！）でお願いします！」と言えば、

Tomei[0]（Tomei【党名】配列の０番目）で「A党」、

Tokuhyou[0]（Tokuhyou【得票】配列の０番目）で「1200」

という、党名と得票数などの取得が容易になります。

せんせ

「党名をキーとした連想配列の方がいいのでは？」というツッコミは無しです。でも、連想配列もそのうち出てくるかもしれませんね。連想配列についてはまたの機会に解説します。

大体どの言語でも、

たろぅ

配列のn番目が欲しいなぁ。

というときには、配列[n番目]という書き方が多いです。

基本的に０スタートなので、このサイトでは「０番目」という言い方をしていきます。

せんせ

一般的には０番目、という言い方はしませんが、例えば「Tomei[0]を配列Tomeiの１番目」というのは混乱しそうなので。

繰り返し処理

繰り返し処理はコンピュータの最も得意とするところです。実際のプログラミングでは

Tokuhyo = [1200,660,1440,180];
sousuu = 0;
for(m = 0; m < Tokuhyou.length; m++){
  sousuu = sousuu + Tokuhyou[m];
}

こんな感じで書いたりします。for(m = 0; m < Tokuhyou.length; m++)の意味は、「変数の初期値：m=0が初期値ですよ」「条件：m < 【Tokuhyou.lengthはTokuhyou配列の長さ=4の意味】である限り繰り返してください」「処理が終わったらmに１加えてください(mに１ずつ加えて、というのをm++と書くことはよくある）」です。

せんせ

このプログラミングの動きは本文からずれるので、興味がある人はご覧ください。

条件分岐

条件による分岐はプログラミングの基本です。実際のプログラミングでは

if(max < Hikaku[i]){
  max = Hiakaku[i];
  maxi = i;
}

などと書きます。条件分岐は意味としてはそこまでわかりにくいものではありません。

ただ、今回のように「条件を満たしたらどういう処理をしたいか」という点に関しては「今、ここでは条件を満たしたときになにをしたいか？」を考えることが重要になります。

まとめ

かなりの長文になってしまいました…。

それだけプログラミングを言葉で説明しようとしたらボリュームがある、ということですね。

「よくわからなかったなぁ」という人は、何度か繰り返し読んで欲しいです。

また、解説を見れば、問題を解く上で「ここではどういう処理をしたいか？」を文脈から読み解くことが重要になることがわかると思います。

次回は、データ処理分野になります。

あわせて読みたい

「情報」が共通テストに課される！？サンプル問題の解説とねらい③ サンプル問題の解説第３弾です。第３問はデータ分析の問題です。 サンプル問題の解説はこれで一通り終わりですが、結果的にかなり幅広い知識が必要になるテストだな、と…

前回の記事はコチラ

あわせて読みたい

「情報」が共通テストに課される！？サンプル問題の解説とねらい① 最近、高校教育業界で話題になっていることがあります。それは2025年度（令和7年度）共通テストで「情報」が課される、という内容です。 令和4年度高校入学生から新たに…