PR
行列はベクトルの変換に使える?行列の積が持つもう一つの側面
行列に行列を掛けると、計算結果として新たな行列が現れます。

このときに新たに現れる行列は、実は元の行列を変換したもの、とみなすことができるのです!
 たろぅ
たろぅ行列の掛け算が変換…?ちょっと何言ってるかわかんない。
となるでしょうが、具体的な例を見ていただけたらわかります。この行列の変換はとても便利&重要なんです!
ということで、この記事では、行列の積が持つ「変換」の意味について説明していきます。
特に行列を使ったベクトルの変換については、解析などでも必要な考え方になるので、理解しておくことをオススメします。
行列によるベクトルの変換を具体的に見てみよう



早速ですが、行列を使った平面ベクトルの変換について、具体的に見ていきましょう!
適当な行列を掛けてみよう
先ほどの記事でも少し紹介していますが、ベクトルを縦長の行列とみなして計算することは、行列の世界ではよくやります。
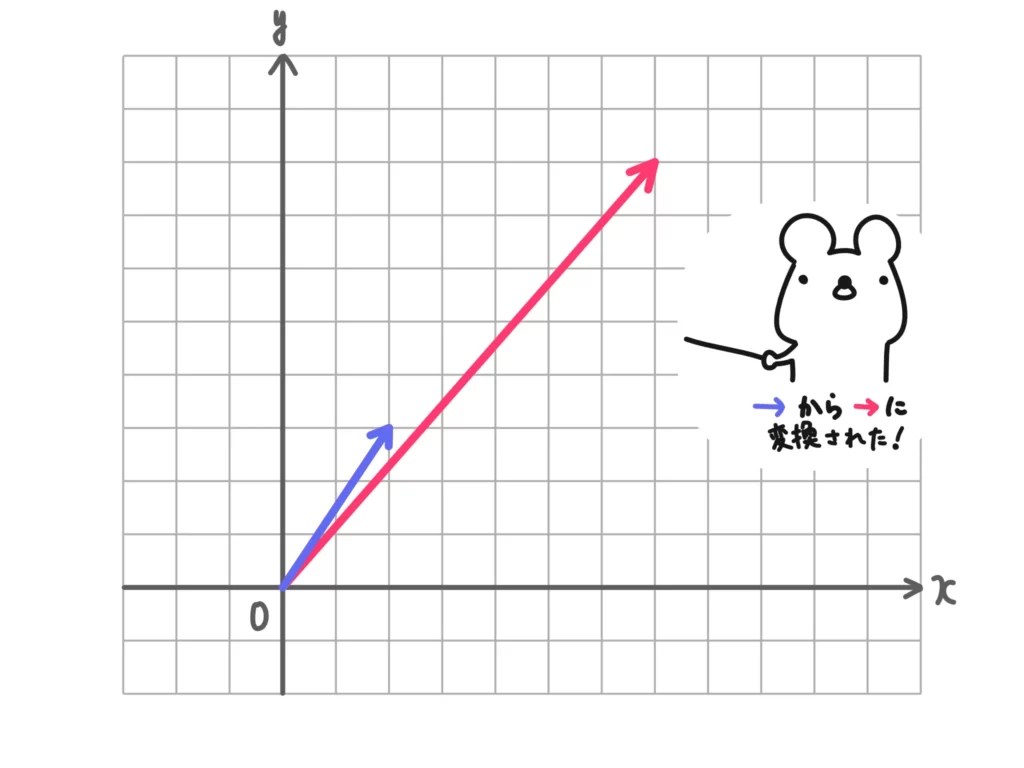
例1.\( \overrightarrow{a} = (2,3)\)を\( \begin{pmatrix} 2 \\ 3 \end{pmatrix}\)と書いたりします。
例えば、このベクトルに適当な行列\(A = \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} \)を左から掛けたとしましょう。
例2.\( \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 4+3 \\ 2+6 \end{pmatrix}=\begin{pmatrix} 7 \\ 8 \end{pmatrix}\)
つまり、行列\(A\)を掛けることでベクトル\( \begin{pmatrix} 1 \\ 2 \end{pmatrix}\)が\( \begin{pmatrix} 7 \\ 8 \end{pmatrix}\)に変換された、とみなせます。




もう少し、色んなベクトルに掛けてみましょう。
例3.やっぱり、単位ベクトル\( \begin{pmatrix} 1 \\ 0 \end{pmatrix}\)、\( \begin{pmatrix} 0 \\ 1 \end{pmatrix}\)に掛けてみたくなりますよね。
\( \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \end{pmatrix}\)
\( \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\)
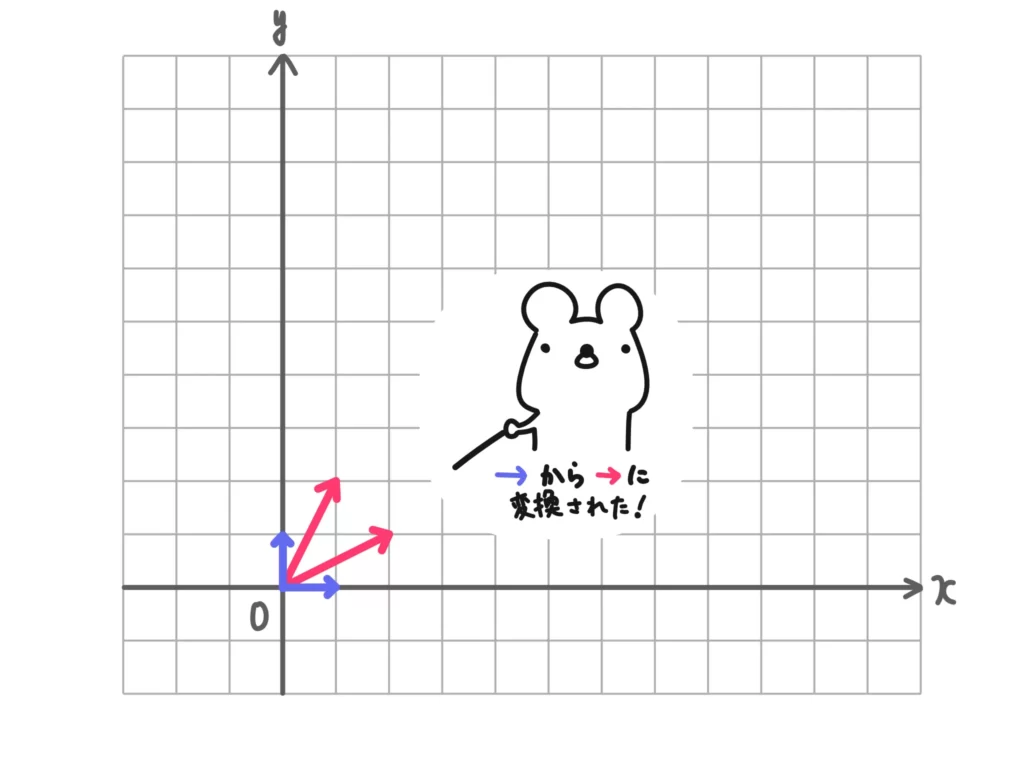

以上の結果から、行列\(A\)によって、座標軸がナナメに歪んで伸びたような感じに変換されることがわかります。
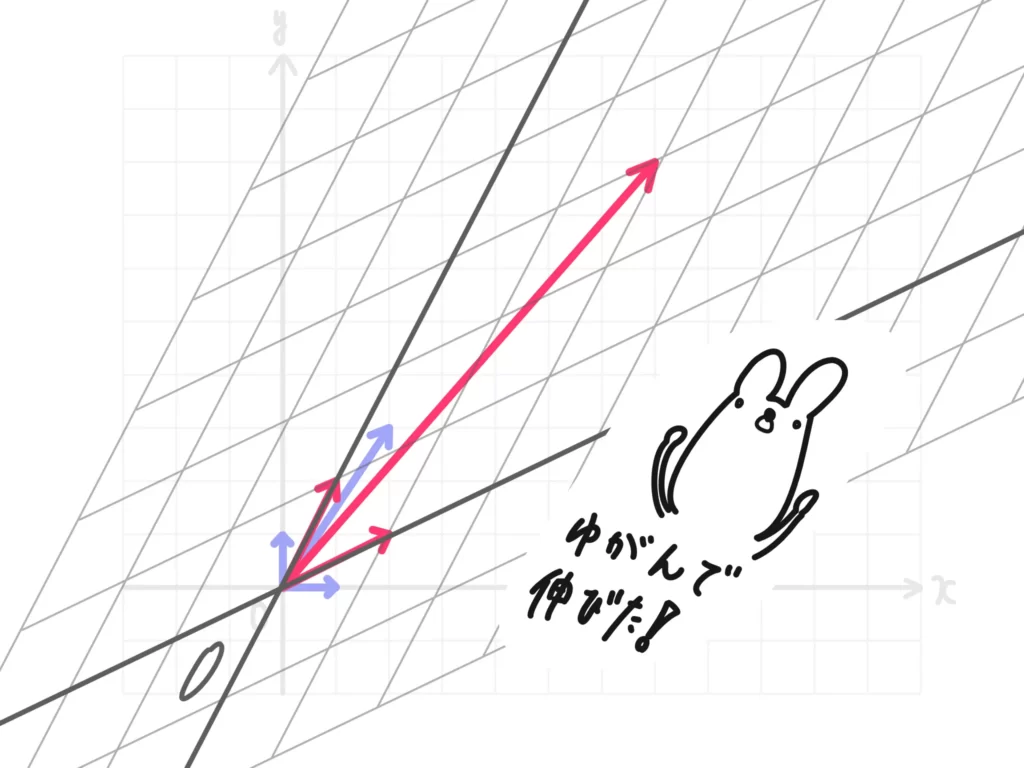

このように、行列を掛けることで、座標軸の変形が起きてベクトルの変換が行われます。
回転を表す行列
行列の積による有名な変換の一つに回転があります。
今の高校数学の教育課程では回転といえば複素数平面ですが、行列の変換でも回転を表現することができます。

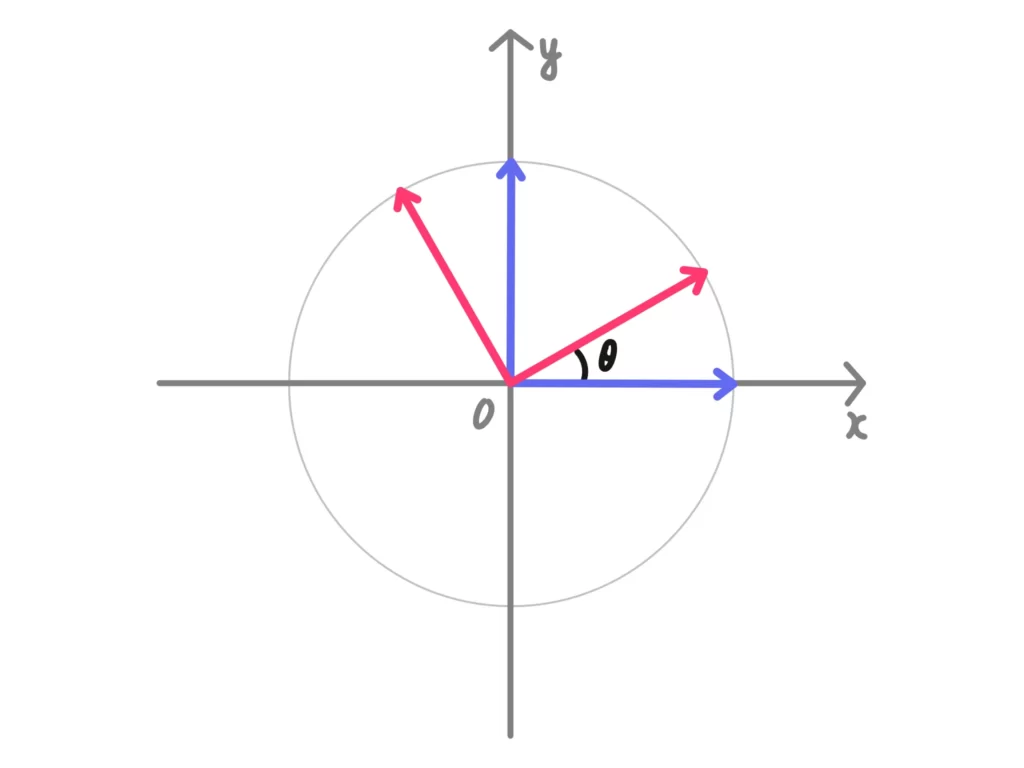
結論からいうと、次の行列を掛けることで\(\theta\)回転を表現することができます。
行列による回転
2次のベクトルに
\( \begin{pmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{pmatrix} \)
を左から掛けることで原点を中心とした\(\theta\)回転の変換となる。




2次のベクトルを\( \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} r\cos{\alpha} \\ r\sin{\alpha} \end{pmatrix}\)の極座標表示にして説明していきましょう。
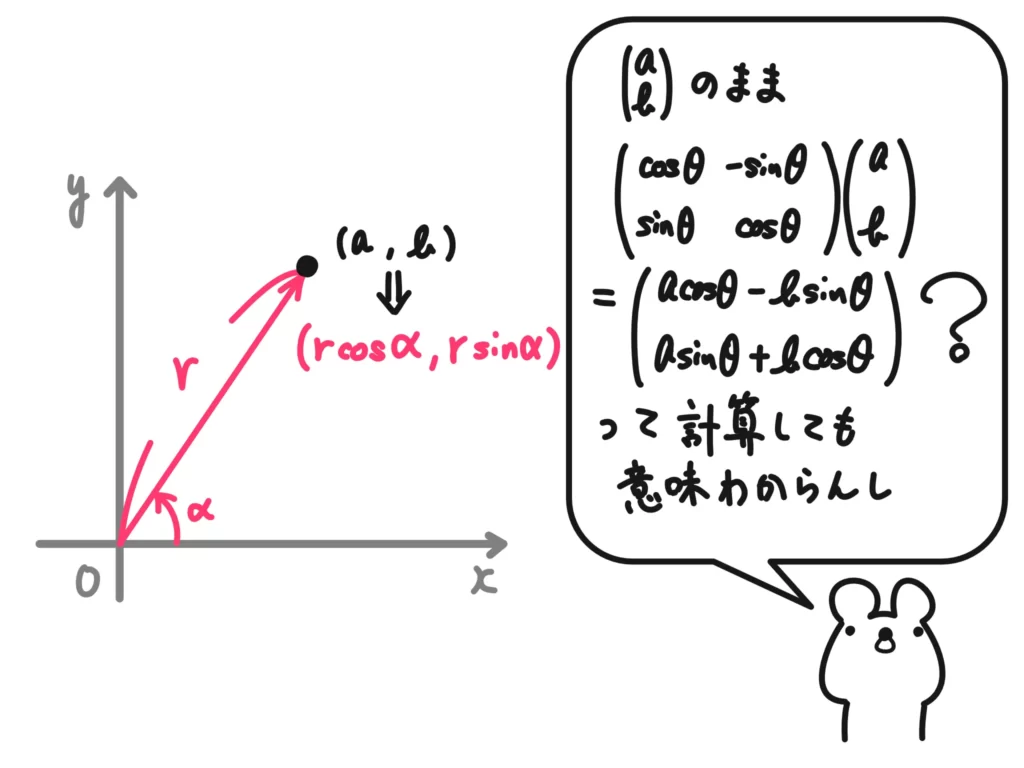

説明、と言っても実際に掛けてみるだけです。
\( \begin{pmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{pmatrix} \begin{pmatrix} r\cos{\alpha} \\ r\sin{\alpha} \end{pmatrix}\)
\( \quad = \begin{pmatrix} \cos{\theta} \cdot r\cos{\alpha}-\sin{\theta} \cdot r\sin{\alpha} \\ \sin{\theta} \cdot r\cos{\alpha} + \cos{\theta} \cdot r\sin{\alpha} \end{pmatrix}\)
\( \quad = \begin{pmatrix} r(\cos{\alpha}\cos{\theta}-\sin{\alpha}\sin{\theta}) \\ r(\sin{\alpha} \cos{\theta}+\cos{\alpha}\sin{\theta}) \end{pmatrix}\)(掛ける順序、足す順序を変えています)
\( \quad = \begin{pmatrix} r\cos{(\alpha+\theta)} \\ r\sin{(\alpha+\theta)} \end{pmatrix}\)
ということで、加法定理を使って偏角\(\alpha\)を\(\alpha+\theta\)に変換することができ、回転を表す行列となります。
変換という側面から見た行列式の意味
こちらの記事でも少し触れていますが、行列式は変換による拡大倍率を表す、という意味もあります。
少し詳しく説明すると、行列式は、変換によってどれだけ座標が引き伸ばされたか?(もしくは縮んだか?反対向きになったか?)を表します。



先ほどの2つの例で確認してみましょう!
例1.行列\(A = \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} \)による変換では、次の図のようになるのでした。


これによって、基準のベクトルが張る平行四辺形(正方形)の面積がどうなったか、確認してみましょう。
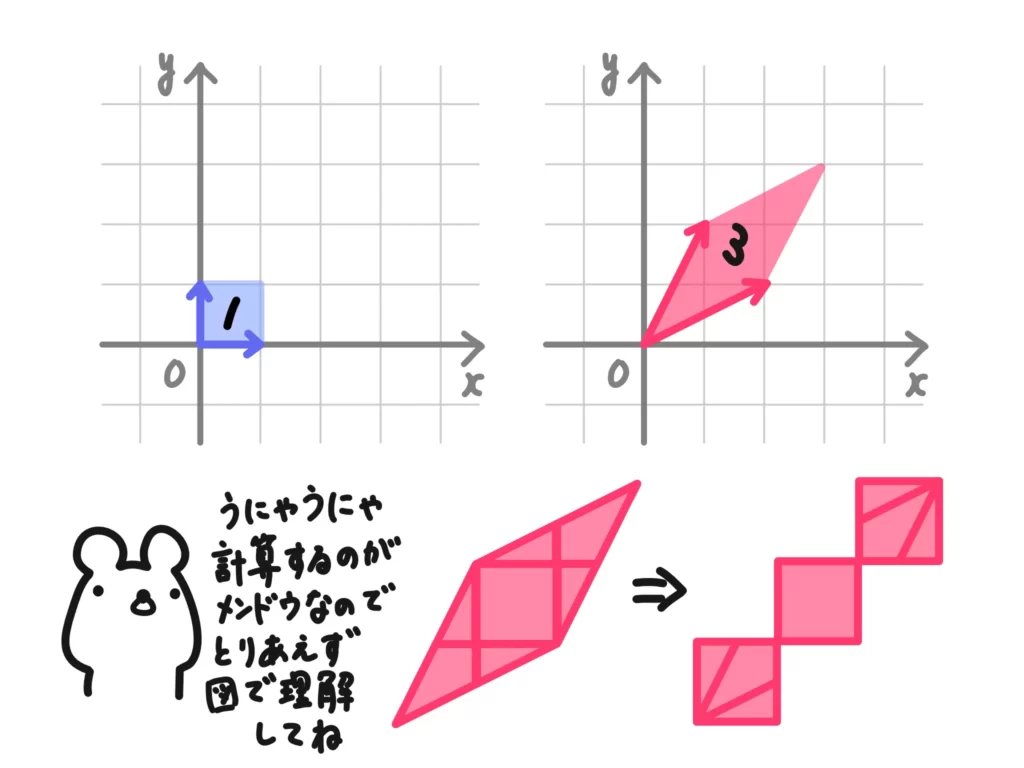




ということで、面積基準で3倍になったことが確認できました!
一応、計算でも面積が3になることを確認しておきましょう。
(確認)
基準のベクトル\(\begin{pmatrix} 1 \\ 0 \end{pmatrix}\)、\(\begin{pmatrix} 0 \\ 1 \end{pmatrix}\)は行列\(A = \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} \)によって、それぞれ\(\begin{pmatrix} 2 \\ 1 \end{pmatrix}\)、\(\begin{pmatrix} 1 \\ 2 \end{pmatrix}\)に変換されます。
このベクトルが張る平行四辺形の面積は、
\(|2\cdot 2 -1 \cdot 1|=3\) …(※)
となります。(ベクトル\(\overrightarrow{a}=(a_1,a_2)\)、\(\overrightarrow{b}=(b_1,b_2)\)が張る三角形の面積が\(\displaystyle \frac{1}{2}|a_1b_2-a_2b_1|\))となるので、その2倍だと思えばOKです。)



計算でも確かに面積は3になりますね!
一方、行列\(A\)の行列式からアプローチしてみましょう。
\(|A|=2 \cdot 2 – 1 \cdot 1 = 3\)
で、こちらも3となっていますね!
さて、ここで気付いた人もいるかもしれませんが、行列式の計算と(※)の平行四辺形の計算は絶対値があるかないかの違いだけで、同じ計算をしていますね。



では、より一般的な行列で、基準のベクトルがどうなるかを計算してみましょう!
\(\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}\)を基準となる単位ベクトル\( \begin{pmatrix} 1 \\ 0 \end{pmatrix}\)、\( \begin{pmatrix} 0 \\ 1 \end{pmatrix}\)に掛けてみます。
\(\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix}=\begin{pmatrix} a_{11} \\ a_{21} \end{pmatrix}\)(←1列目だけ取り出せた)
\(\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}\begin{pmatrix} 0 \\ 1 \end{pmatrix}=\begin{pmatrix} a_{12} \\ a_{22} \end{pmatrix}\)(←2列目だけ取り出せた)
なので、\(\begin{pmatrix} a_{11} \\ a_{21} \end{pmatrix}\)と\(\begin{pmatrix} a_{12} \\ a_{22} \end{pmatrix}\)が張る平行四辺形の面積は、
\(|a_{11}a_{22}-a_{12}a_{21}|\)
となり、行列式\(a_{11}a_{22}-a_{12}a_{21}\)に絶対値をつけた値になります。
元の基準となるベクトルが張る平行四辺形(正方形)の面積は1なので、行列式は行列による(符号付きの)拡大倍率を表すことになります!
例2.回転行列の場合
ここまでの話でわかったと思いますが、回転だけだったら、拡大倍率は1(面積変化なし)となるはずです。
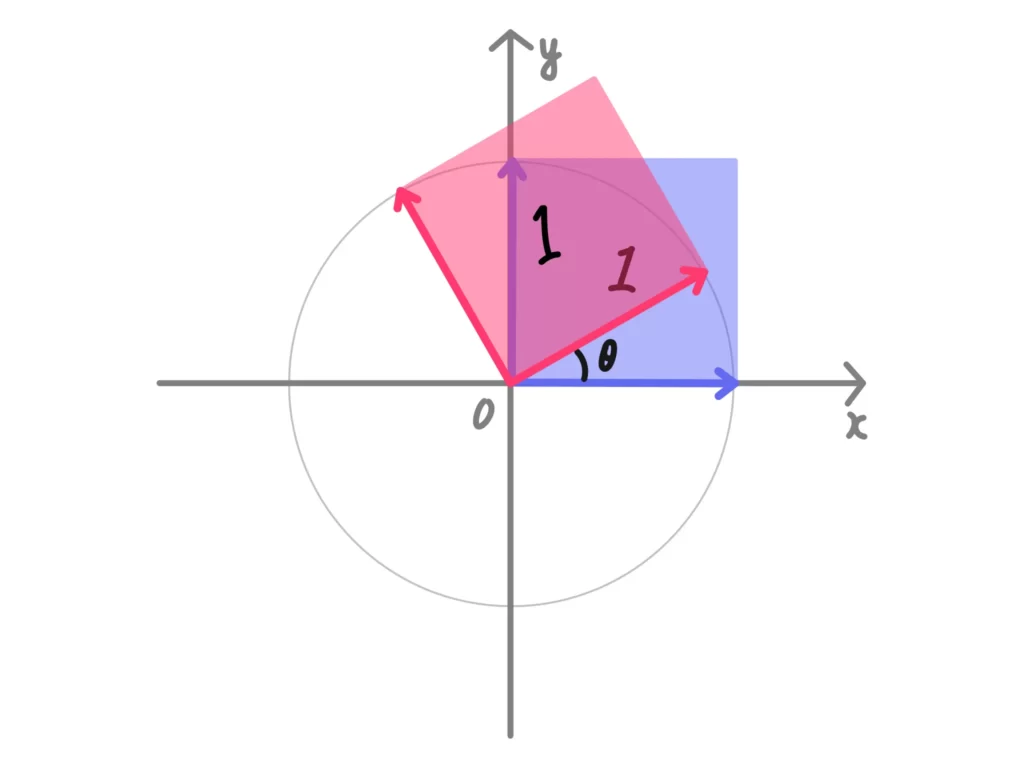

試しに回転行列\( \begin{pmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{pmatrix} \)の行列式をとってみましょう。
(行列式)\(=\cos{\theta}\cdot \cos{\theta}-(-\sin{\theta})\cdot \sin{\theta}\)
\(\quad =\cos^2{\theta}+\sin^2{\theta}=1\)
となり、やはり拡大倍率は変わらないことがわかります!



イメージと計算が一致するのは面白いし、気持ちいいですね!
まとめ
行列の積が変換を表すことの説明でした。
行列の積を考察すると、座標が「歪んだり」「伸びたり」「回転したり」していることがわかるのは面白いですね。
また、行列式が変換率を表している、というイメージをもっておくと、重積分の変数変換のときに役に立つので頭の片隅においておきましょう。



