ベクトルの足し算は平行四辺形！？【和の重要な合成のイメージ】

2023年10月22日

ベクトルは便利で重要な考え方ですが、苦手な人が多い分野でもあります。

原因は「イメージ」と「その場での思考」が重要だからです。

たろぅ

その状況に応じた対応って苦手…。

ですが、その分覚えることも少ないですし、基本的なイメージをしっかりと掴むことができればあとはちょっと練習するだけでベクトルの理解はかなり深まります。

せんせ

要は最初の本質部分が大事！
「ベクトルは感覚だ！」

この記事では、ベクトルの基本「ベクトルの和」について重要なイメージの説明をしていきます。

ベクトルの和とは？

たろぅ

お腹すいたなぁ…コンビニに行って肉まんでも買って食べようかな。肉まんの美味しい季節になってきたぜ。

はなこ

あ！たろう君！ちょっと！

たろぅ

（嫌な予感…）はい、なんでしょう…？

はなこ

ちょっとコンビニに行く前にこの本、図書館に返してきてよ。返却ボックスに入れるだけだから。

たろぅ

え…。図書館って逆方向じゃん。

はなこ

ふーん…。この間の借りをチャラにする代わりに「１年間なんでも言うこときく」っての忘れたんだ…。へー…。ほー…。

たろぅ

…図書館、行かせていただきます。

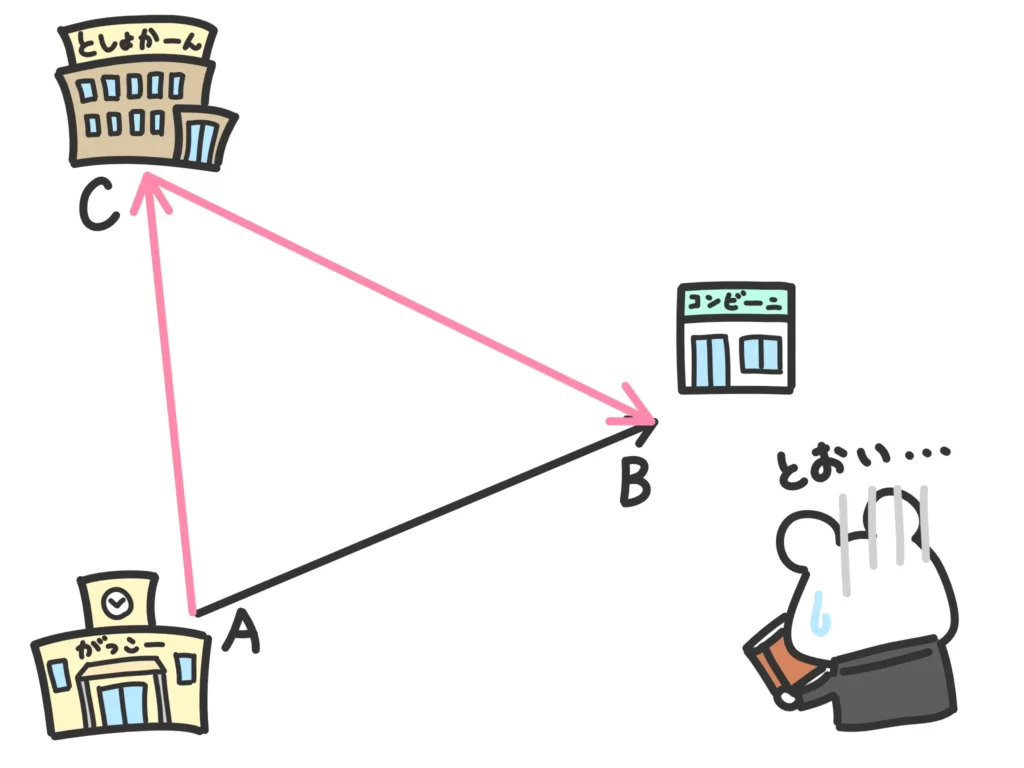
ということで、「ベクトルの和」です。

そこまで難しい話ではないのですが、最後の「合成と平行四辺形のイメージ」は重要なので押さえておいてください。

ベクトルの和

\(\overrightarrow{AB} = \overrightarrow{AC} + \overrightarrow{CB}\)

図を使った「ベクトルの和」

せんせ

まずは図で「ベクトルの和」をイメージしていきましょう。

一番わかりやすいイメージで言うと、「ベクトルの先っちょに他のベクトルを継ぎ足す」という感じですね。

先ほどの図のように、\(\overrightarrow{AC}\)の先に\(\overrightarrow{CB}\)を継ぎ足すことで\(\overrightarrow{AB}\)を表現することができます。

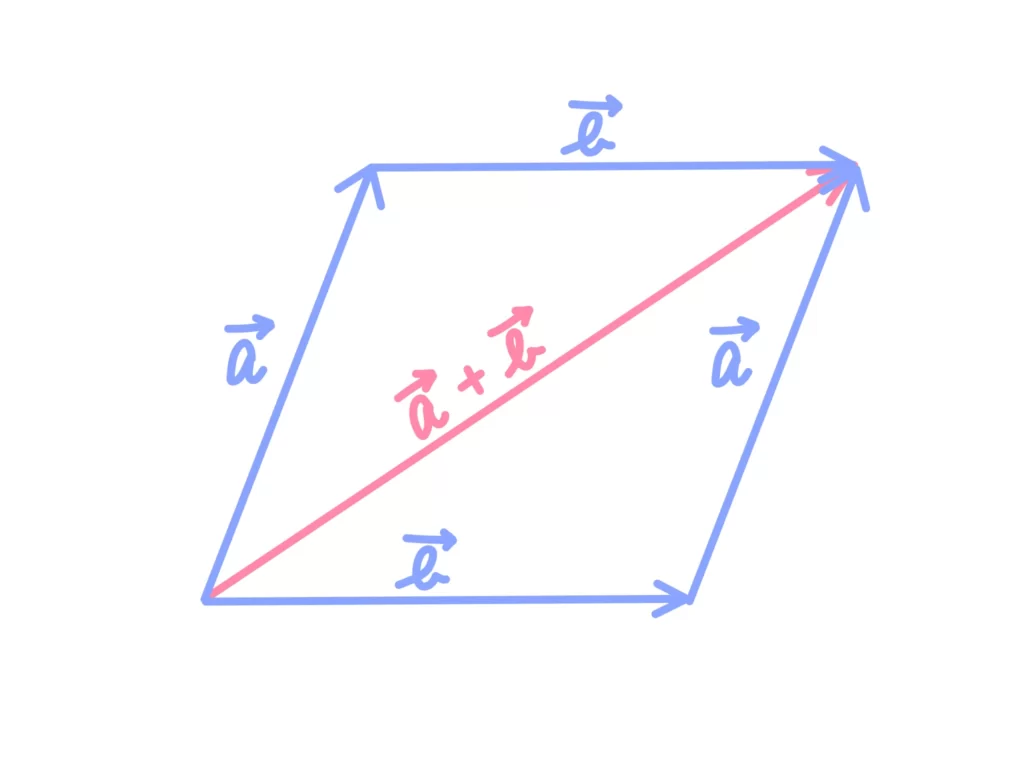
また、次の図のように\(\overrightarrow{a}\)、\(\overrightarrow{b}\)を定めると、\(\overrightarrow{a}+\overrightarrow{b}\)も\(\overrightarrow{b}+\overrightarrow{a}\)も同じであることがわかります。

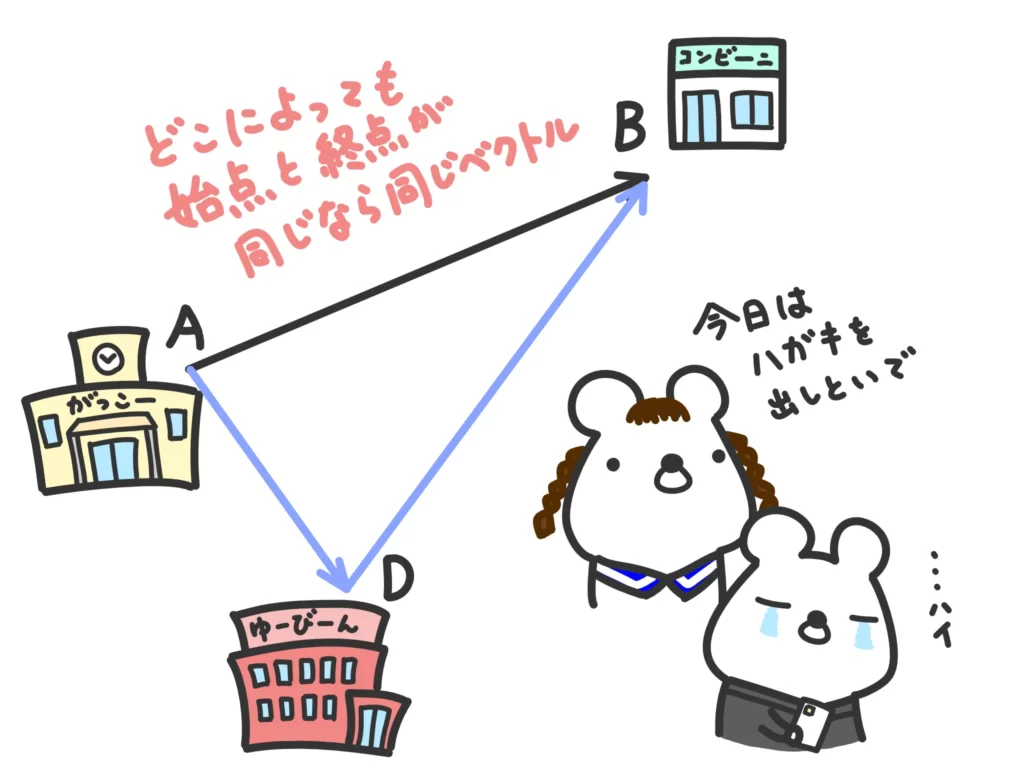
また、ベクトルは始点と終点が同じであれば同じベクトルなので、途中でどこかに寄り道をしても結果始点と終点が同じであれば同じとみなせます。

成分を使った「ベクトルの和」

成分表示についてはこちらの記事も合わせてご覧ください。

ベクトルの和と合成のイメージ

ここまでの話では、ベクトルの和は「ベクトルの先っちょに他のベクトルを加える」というイメージで進めてきましたが、ベクトルの和を理解するために、もう一つ別の重要なイメージがあります。

それは、「始点を揃えたときに、二つのベクトルが作る平行四辺形の対角線が和になる」というイメージです。

せんせ

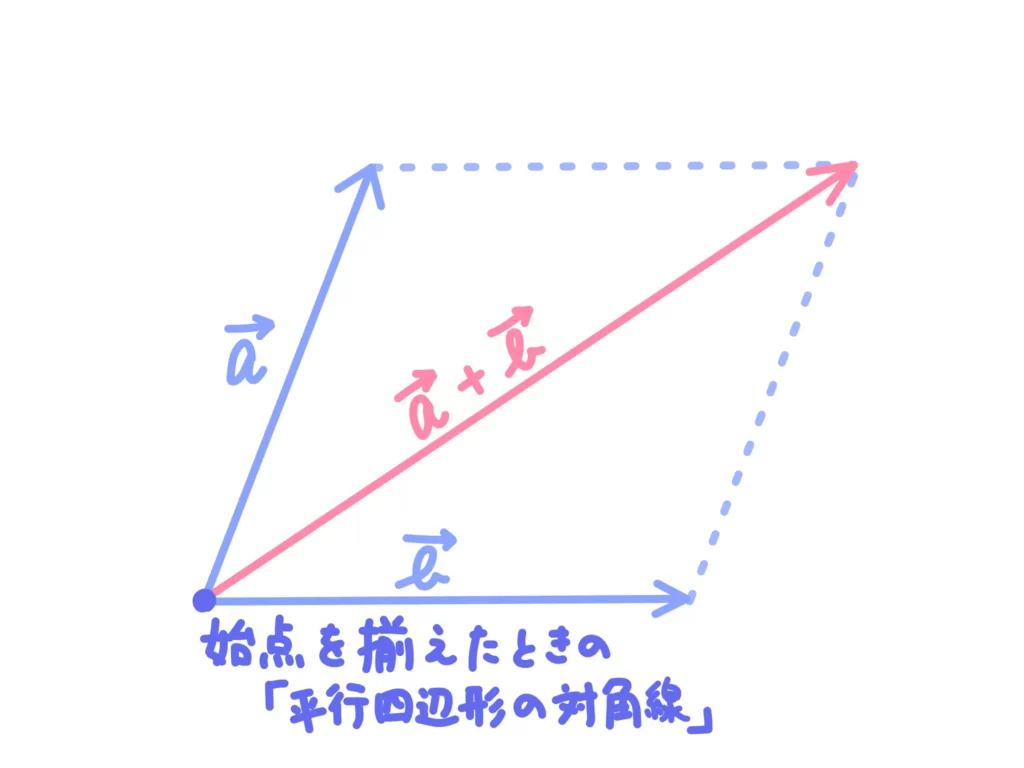
今後何度も出てくると思いますが、「始点を揃える」という作業はめちゃくちゃ重要です！
ベクトルは自由度が高い分、始点を揃えていないと訳が分からなくなります（＝問題が解けなくなります）。

ということで、「始点を揃えた状態でのベクトルの和」の感覚はこの先重要になってくるので押さえておいてください。

まとめ

ベクトルの基本、ベクトルの和についての説明でした。

「始点を揃えたときに、二つのベクトルが作る平行四辺形の対角線が和になる」というところは押さえておいてください。