分散はなぜ２乗？求め方や意味をわかりやすく説明

2022年9月20日2023年6月6日

分散は統計で出てくるデータの代表値ですが、その意味はご存じでしょうか？

「そんなの知ってる！」という人も「何のこっちゃ…」という人もいると思います。では、分散に関する次の質問はどうでしょう？

「なんで分散の計算をするときに、わざわざ『偏差の2乗』の平均値をとるのですか？」

「？（だって…そう習ったから…）」という人が多いんじゃないでしょうか？

この記事では分散（と標準偏差）の意味と求め方、なぜわざわざ偏差の2乗の平均値をとるのか？など、分散に関する疑問を解説していきます。

このブログで活躍してるクマのLINEスタンプもあります！

分散とは？求め方を説明

たろぅ

せんせい、質問です！

せんせ

はい、どうぞ。

たろぅ

なんで分散なんか使うんですか？計算が大変な割に、意味がよくわかんなかったんですけど…。

せんせ

分散は簡単に言うと、「散らばり具合」を表す値なんですが…そのあたりをもう少し詳しく説明しましょうか。

たろぅ

お願いします！

早速ですが、分散の求め方は次のようになります。

分散と標準偏差

\(n\)個のデータ\(x_1\)、\(x_2\)、…、\(x_n\)の平均を\(\bar{x}\)とすると、分散\(s^2\)は

分散：\(\displaystyle s^2 = \frac{1}{n} \{ (x_1-\bar{x})^2 + (x_2-\bar{x})^2 + \cdots + (x_n-\bar{x})^2 \} \)

で計算できます。また、\( \sqrt{（分散）}\)のことを標準偏差\(s\)といいます。

標準偏差： \(\displaystyle s =\sqrt{ \frac{1}{n} \{ (x_1-\bar{x})^2 + (x_2-\bar{x})^2 + \cdots + (x_n-\bar{x})^2 \} } \)

ちなみに、自分自身のデータから平均を引いた\(x_n-\bar{x}\)のことを偏差といいます。

ですので、分散は日本語でいうと「\(（偏差）^2\)の平均」をとったもの、といえます。

たろぅ

んー…、これにどんな意味があるんですか？さっき「散らばりを表す」って言ってましたけど…。

せんせ

では分散の意味を説明しましょうか。

分散の意味って？

結論からいうと、分散は「そのデータがどれだけ散らばっているか？」を示す値です。名前そのままですね。

分散が「散らばり」を表す値、と言われても基準がないとわかりませんよね？そこで、わかりやすく、基準を「平均」とします。

せんせ

つまり、平均からどれだけ散らばっているのか？を数値化しちゃおう、ということです。そこで、先ほどの偏差を使うんですね。

偏差は「自分自身が平均からどれだけ離れているか？」を単純な引き算で表したものです。「（自身のデータ）ー（平均）」で計算します。

例えば「平均点５点の小テスト」に対して自分自身の点が「７点」だった人と「３点」だった人がいるとしましょう。

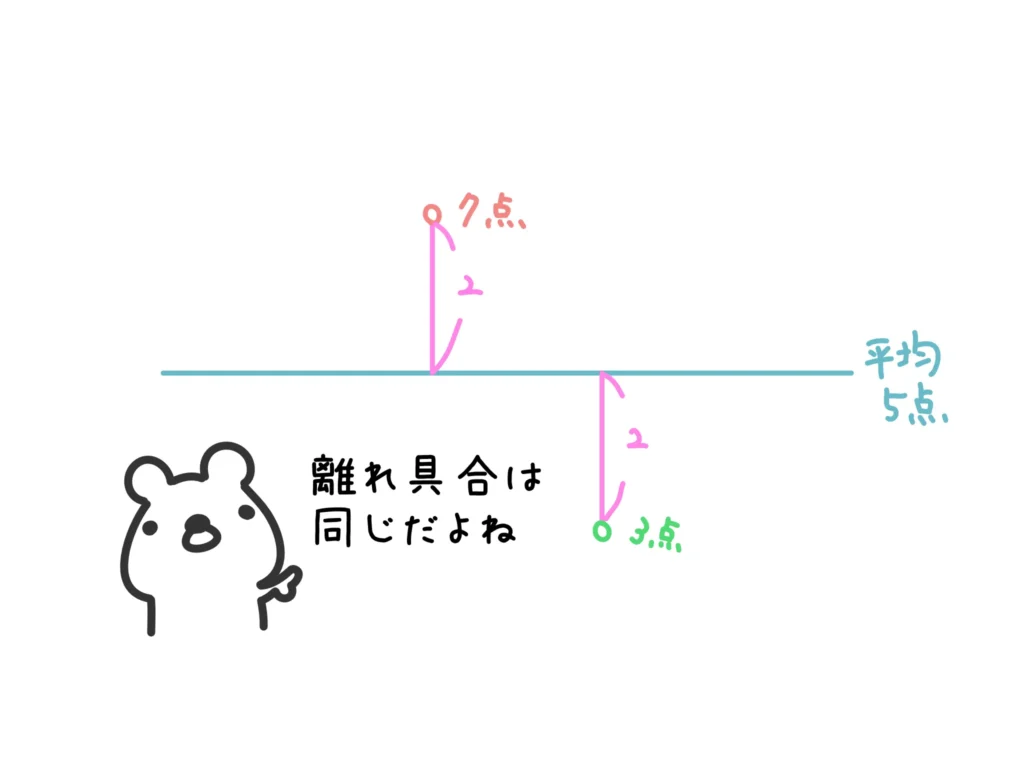
この人たちは、偏差でいうと「＋２」と「−２」という違う値になりますが、「平均からの離れ具合」という意味では「どちらも２離れている」ということで、できれば同じ値として扱ってやりたいところです。要は「離れ具合」を表したいので＋（プラス）やー（マイナス）は関係ないんですね。

解決策として、手っ取り早く偏差を二乗してやります。二乗することで、\((+2)^2=4\)、\((-2)^2=4\)、となり「離れ具合」を表す値として適切なものが得られました。

たろぅ

なるほど…二乗することで、平均から「＋」の方に離れていようが「ー」の方に離れていようが同じ＋（プラス）の値として計算できるんだな。

これで、「\(（偏差)^2\)は各データの離れ具合を表す値」という意味になったので、その平均をとれば、散らばり具合を表す値になります。

たろぅ

…

せんせ

どうしました？

たろぅ

分散が散らばり具合を表す、っていうのはわかったんですけど、なんかいくつか疑問が出てきました…。

せんせ

どーぞ、なんでも答えますよ。

疑問１．そもそもなぜ「散らばり」が重要なの？

たろぅ

大体、なんでわざわざこんな面倒な計算してまで「散らばり具合」を測るんですか？

せんせ

では、実際に次のデータを見てみましょう。小テストのデータです。どちらも「平均は５点」です。

英語	Aさん	Bさん	Cさん	Dさん	Eさん	平均
得点	5	4	5	6	5	5
\(（偏差）^2\)	0	1	0	1	0	0.4

数学	Aさん	Bさん	Cさん	Dさん	Eさん	平均
得点	1	9	5	0	10	5
\(（偏差）^2\)	16	16	0	25	25	16.4

たろぅ

同じ平均5でも随分様子が違いますね…。英語は平均近くにデータが揃ってて、数学はバラバラです。確かに分散の値（\(（偏差）^2\)の平均）も数学が高いです。

せんせ

それももちろんそうなんだけど、じゃあ、例えばたろう君が英語も数学も10点を取ったとしましょう。まぁ、仮に、万が一、ですが…。

たろぅ

（そこ、強調しなくて良くね？）はい、それで？

せんせ

どっちの10点が価値が高いと思います？

たろぅ

ん？同じ10点なのに価値の差があるんですか？

せんせ

まぁあくまでデータ分析的に、ですがね。

たろぅ

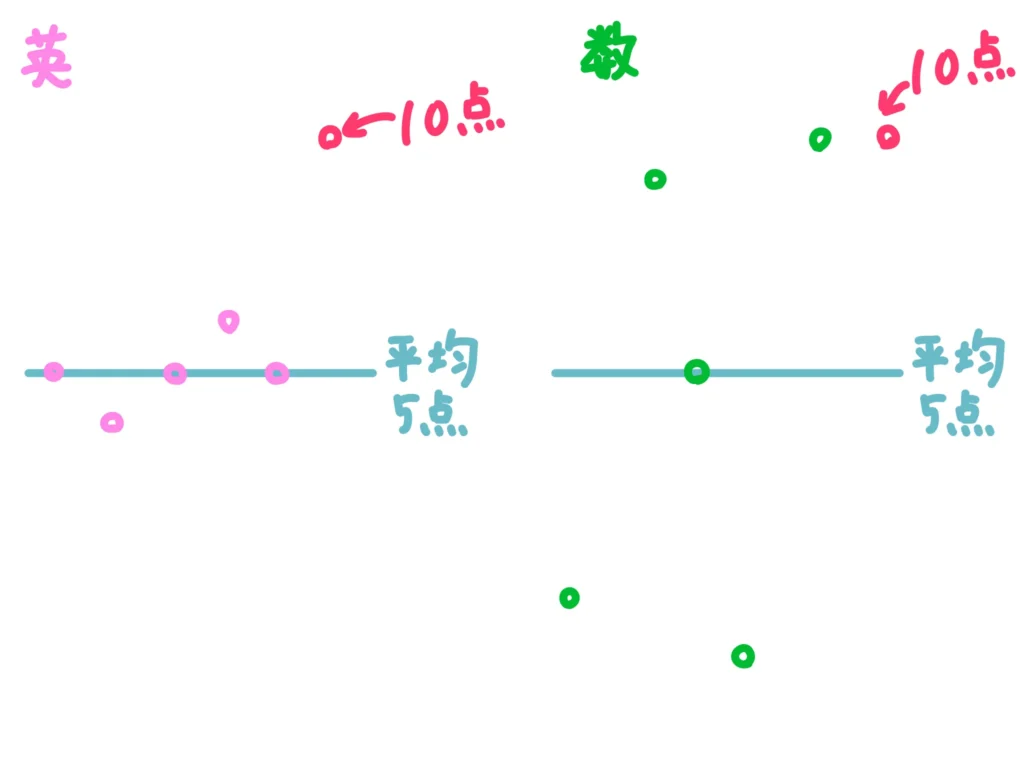
はぁ…言われてみると、数学の10点より英語の10点の方が価値がある気がしますね。

せんせ

なぜですか？

たろぅ

数学は他にも10点取ってる人もいるし、9点とかもいますよね。それに対して英語は高得点を取ってる人がいないです。そこの「10点」はインパクトが大きいと思います。

これがまさに「偏差値」の考え方ですね。

偏差値は、平均点＝50として、分散の大きい小さい（正確には標準偏差）を加味した上で、自分の得点の価値を測る計算方法です。なので、同じ得点でも偏差値が違うんですね。

このように「データの散らばり」を知ることは、そのデータの様子や相対的な意味合いを考える上で重要です。

たろぅ

なるほど、納得です！

なぜ２乗するの？

たろぅ

あと、計算方法もなんか納得いきません。はっきり言って二乗するのが面倒です！

せんせ

まぁ、そうなんだけどね…でも二乗したほうがいいんですよ…。

偏差をそのまま平均してみよう

たろぅ

偏差をそのまま平均したら早いんじゃないですか？

せんせ

それは全く意味ないですね。0になります。

たろぅ

あら？そうなの？

偏差をそのまま平均しても意味はないです。

日本語で説明するなら、偏差は＋（プラス）ー（マイナス）付きの平均からの差です。当然その差の平均をとってしまえば0になります。

数式で説明するなら、

\(\displaystyle \frac{1}{n} \{ (x_1-\bar{x})+(x_2-\bar{x})+\cdots +(x_n-\bar{x}) \} \)

\(\displaystyle = \frac{1}{n} \{ (x_1+x_2+ \cdots +x_n) – n \cdot \bar{x} \} \)（← \( \bar{x}\)は\(n\)個ある）

\(\displaystyle = \frac{1}{n} (x_1+x_2+ \cdots +x_n) – \frac{1}{n}\cdot n \bar{x} \)（← \(\displaystyle \frac{1}{n}\)を展開）

\(\displaystyle = \bar{x} – \bar{x} =0 \)（← \(\displaystyle \frac{1}{n} (x_1+x_2+ \cdots +x_n)=\bar{x}\)だから）

絶対値使ってみたら？

たろぅ

はい！次はマジでいい考えです！
絶対値使ったらどうでしょう？

せんせ

あー…うん、まぁねぇ…。

たろぅ

絶対それの方が早いですし、離れ具合を＋（プラス）で表現すればいいんだからこれが一番ですよ！

せんせ

では、先ほどの例でやってみましょう。

英語	Aさん	Bさん	Cさん	Dさん	Eさん	平均
得点	5	4	5	6	5	5
\|偏差\|	0	1	0	1	0	0.4
\(（偏差）^2\)	0	1	0	1	0	0.4

数学	Aさん	Bさん	Cさん	Dさん	Eさん	平均
得点	1	9	5	0	10	5
\|偏差\|	4	4	0	5	5	3.6
\(（偏差）^2\)	16	16	0	25	25	16.4

たろぅ

ほら、いい感じじゃないですか！これでいきましょう！

せんせ

これでいきましょう！…って。
でも、実際は二乗してる方がより分散の特徴を表してるんですよね…。

たろぅ

ん？どういうことですか？

実は、\(（偏差）^2\)の平均の方が、より分散の特徴が出る計算方法になります。

なぜなら二乗することで「平均に近いものはより小さく、平均から遠いものはより大きく」なるからです。

分散は二乗して計算しているので、そのあと\(\sqrt{\quad}\)をとって値を均（なら）します。これが標準偏差の意味ですね。要は二乗したものを戻す「単位合わせ」になります。

せんせ

先ほどの計算結果を標準偏差ベースで比較してみましょう。

	英語	数学
｜偏差｜の平均	0.4	3.6
標準偏差	\(\sqrt{0.4} = 0.6325\)	\(\sqrt{16.4} = 4.05\)

たろぅ

んー…確かに、二乗することでばらつき具合が強調されてる感じがしますね。

せんせ

小テストくらいだったらあまり差は出ませんが、もっと数値が細かかったりすると結構顕著に出ますね。
なので、面倒でも二乗した方がばらつきの特徴がよくでる、ということですね。

たろぅ

んー…面倒だけど仕方ないのか…。

せんせ

実際にはパソコンとかで計算するのであまり問題にならないんですよね。それよりも実用性重視です。

おまけ．もう一つの分散の求め方と使える状況

分散には、もう一つの求め方がありますので、使える状況と一緒に説明します。

分散は「（変数の二乗の平均）ー（平均の二乗）」で計算できます。

分散：\(\displaystyle s^2 = \frac{1}{n} ( x_1^2 + x_2^2 + \cdots + x_n^2 )- \left\{ \frac{1}{n} ( x_1 + x_2+ \cdots + x_n) \right\}^2 \)

これは、平均のキリが悪いときなんかに使いやすいです。あとは各変数の絶対値があまり大きいと使いにくいです。

（証明）

\(\displaystyle s^2 = \frac{1}{n} \{ (x_1-\bar{x})^2 + (x_2-\bar{x})^2 + \cdots + (x_n-\bar{x})^2 \} \)

\(\displaystyle = \frac{1}{n} \{ (x_1^2-2 x_1 \bar{x}-\bar{x}^2) + (x_2^2-2 x_2 \bar{x}-\bar{x}^2) + \cdots + (x_n^2-2 x_n \bar{x}-\bar{x}^2) \} \)（←二乗を展開）

\(\displaystyle = \frac{1}{n} \{ (x_1^2+x_2^2+\cdots+x_n^2)-2 \bar{x}(x_1+x_2+\cdots+x_n)+n \cdot \bar{x}^2\} \)（←それぞれの二乗を展開したときの第１項、第２項、第３項でまとめた）

\(\displaystyle = \frac{1}{n} (x_1^2+x_2^2+\cdots+x_n^2)-2 \bar{x} \cdot \frac{1}{n}(x_1+x_2+\cdots+x_n)+\bar{x}^2 \)（←\(\displaystyle \frac{1}{n}\)を展開）

\(\displaystyle = \frac{1}{n} (x_1^2+x_2^2+\cdots+x_n^2)-2 \bar{x} \cdot \bar{x} + \bar{x}^2 \)

\(\displaystyle = \frac{1}{n} (x_1^2+x_2^2+\cdots+x_n^2)-2 \bar{x}^2 + \bar{x}^2 \)

\(\displaystyle = \frac{1}{n} (x_1^2+x_2^2+\cdots+x_n^2)-\bar{x}^2\)

\(\displaystyle s^2 = \frac{1}{n} ( x_1^2 + x_2^2 + \cdots + x_n^2 )- \left\{ \frac{1}{n} ( x_1 + x_2+ \cdots + x_n) \right\}^2 \)（終）

それこそ小テスト、なんかですね。基本的には\(（偏差）^2\)の方が値としては小さくなるので、普通に計算した方が早いケースが多いです。

一つだけ例を挙げてみましょう。

英語	Aさん	Bさん	Cさん	Dさん	Eさん	平均
得点	5	4	5	6	7	5.4
偏差	-0.4	-1.4	-0.4	0.6	1.6
\(（偏差）^2\)	0.16	1.96	0.16	0.36	2.56	1.04

平均のキリが悪いので、いちいち\(（偏差）^2\)を計算するのが大変です。

これに対して、先ほどの計算方法で計算すると、

英語	Aさん	Bさん	Cさん	Dさん	Eさん	平均
得点	5	4	5	6	7	5.4
\(（得点）^2\)	25	16	25	36	49	30.2

よって、\( 30.2-5.4^2=1.04\)になります。

まぁ、あんまり手間は変わりませんかね…。

勉強が終わったらちょっと一息…Youtubeもやってます！バイクで走りながら大分を楽しく紹介中！ぜひご覧ください。

まとめ

分散の意味、計算方法、その他疑問になりそうなことをまとめました。

特に分散の意味についてはしっかりと理解してほしいな、と思います。

分散は散らばりを上手く表現している計算方法なんだ、と思っておいてください。