PR
弧度法とは？【変換？覚え方？弧度法の意味や使い方がすべてわかる】
弧度法は数学Ⅱの三角関数の最初に習います。
簡単に説明すると、弧度法は角度の表し方なんですが…
たろぅなんで弧度法とか使うの？今までの°（度）じゃダメなの？
と思うかもしれません。
この記事では、弧度法の定義から、なぜ弧度法が必要なのか？そして皆さんが一番気になる弧度法の覚え方について説明していきます。
目次
弧度法とは？
はなこ…このアップルパイ切り分けたの誰？
たろぅぼくだよー。食べやすいと思って。気が利くでしょ？褒めてもいいんだよ？
はなこ…ぜんぜん大きさが違うんだけど。
たろぅほう…大きさ。ははぁん…なるほど…。
はなこ…なによ？切るならちゃんと六等分に切りなさいよ。
たろぅさては、はなこさん、アレだな？細かい性格でしょ？
はなこ……はぁ？？
たろぅ…すいませんでした。
ということで、弧度法です。
さて、皆さん、ホールのアップルパイ（ケーキでもピザでもなんでもいい）を六等分に切る方法を知っていますか？
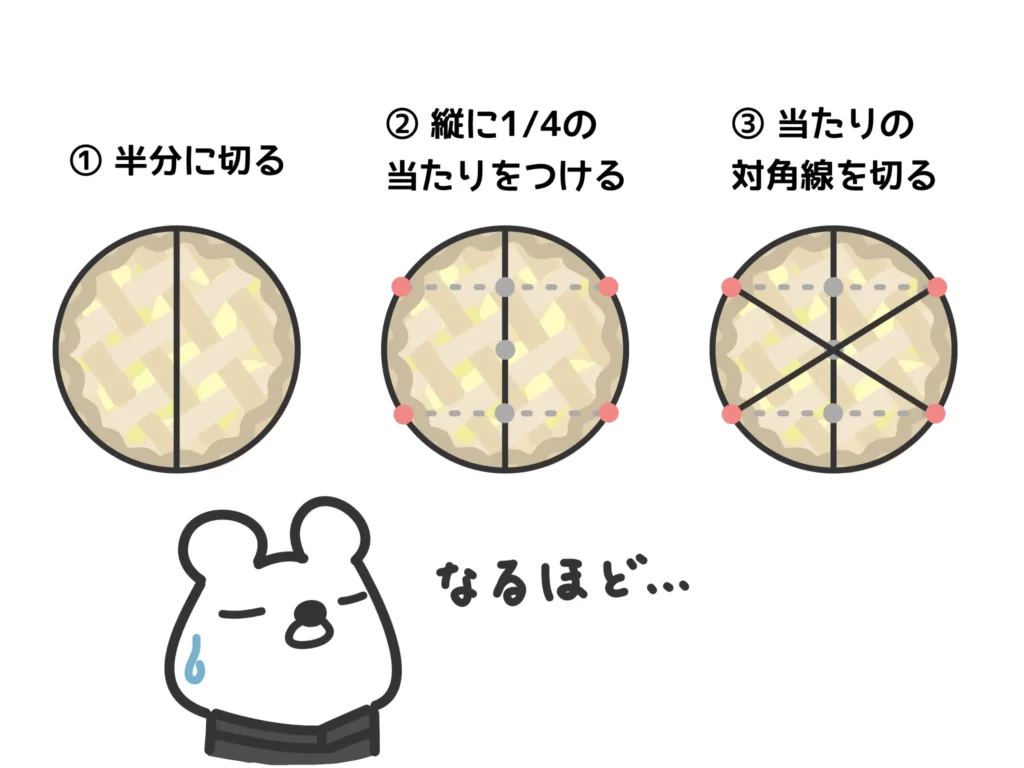
これは、三角比の\(\displaystyle \sin{60°}=\frac{1}{2}\)だからですね。逆に\(\displaystyle \frac{1}{2}\)となるラインで切れば60°が測れる、というお話です。
たろぅなるほど…パイをキレイに切り分けるにはこうすればいいのか…。
なぜいきなりパイを切る話をするのか…。実はこのパイを切る感覚が弧度法において重要な感覚になってくるんです。
弧度法の定義
では、弧度法とはなんなのでしょうか？
結論から言うと、角の大きさの表し方の一つなんですが、これの定義と、なんでこんなものを使うのか？というのと、使い方がわかりにくいんですよね。
せんせということで、この記事では弧度法の基本を徹底的に解説していきます。
突然ですが、扇形の中心角の大きさは弧の長さと比例関係にあります。
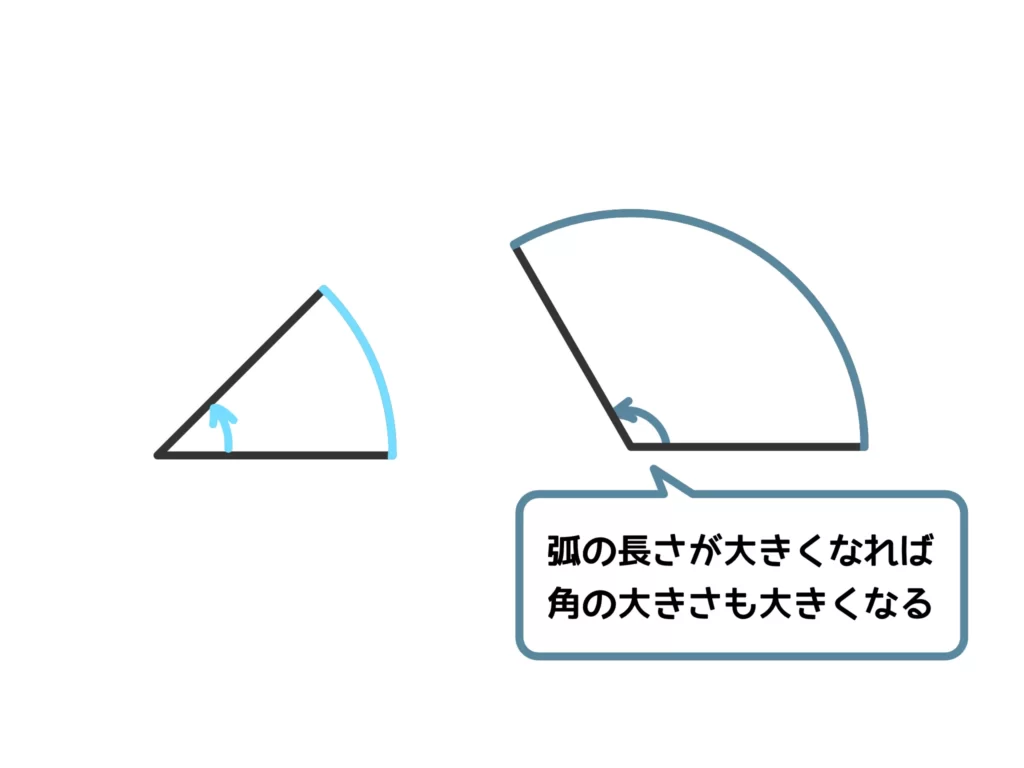
せんせ弧が長くなれば中心角も大きくなる、ということですね。
ということで、弧の長さと半径の比を角の大きさとして利用しよう、という考え方が弧度法です。
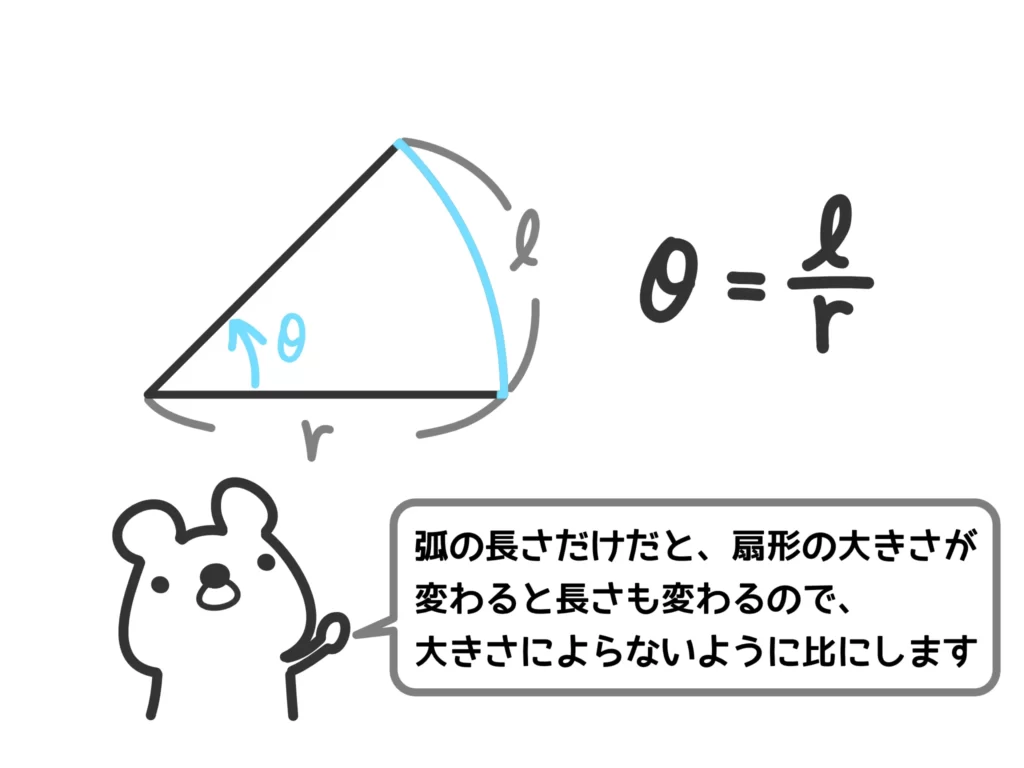
弧度法の定義
半径\(r\)の扇形の弧の長さ\(l\)のときの中心角\(\theta\)を
\(\displaystyle \theta = \frac{l}{r}\)（ラジアンor弧度という）
とする。つまり、弧の長さが半径の長さ\(r\)と等しいとき、
\(\displaystyle \theta = \frac{r}{r} = 1\)（ラジアンor弧度）
となる。
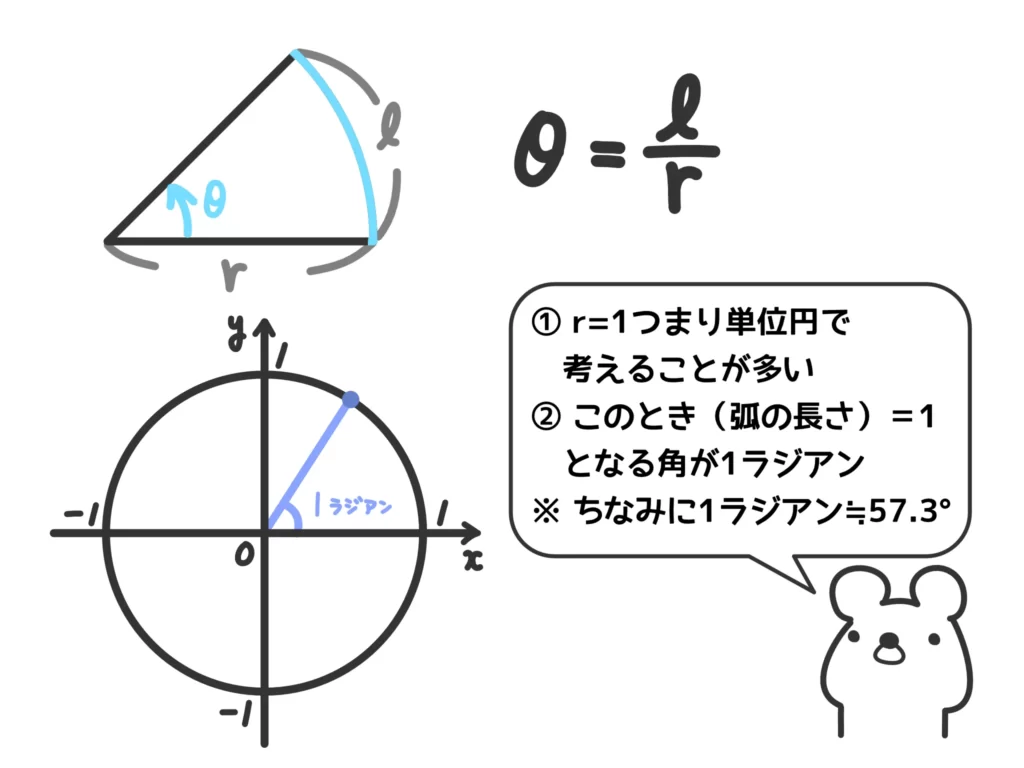
※ 以下では「ラジアン」を使いますが、実際には単位を言わないことも多いです。
ただ、こちらも三角比の定義と一緒で、どんな大きさの扇形を使ってもOKなのですが、やはり統一性がないですしわかりにくいです。
なので、普通は\(r=1\)の扇形を考えます。
せんせ実は1（ラジアン）という弧度の値はほとんど使いません。やはり「有名角に相当する弧度がいくらか？」が気になるところです。
ということで、\(r=1\)の扇形の弧の長さについて考えていきます。このとき、\(\displaystyle \theta = \frac{l}{r}=\frac{l}{1}=l\)（ラジアン）となるので、「弧の長さ」=「弧度法の角の値」となることに注意しましょう。
せんせ\(r=1\)のとき「弧の長さ」=「弧度法の角の値」なので、わかりやすい弧の長さを調べてみましょう。
よくやるのが、中心角180°の扇型の弧の長さを調べる、という方法ですが、結局半径\(1\)の円周を調べるので、まずは半径\(1\)の円の円周を計算します。
半径\(1\)の円の円周は\(2 \pi \cdot 1 = 2 \pi \)なので、このときの弧度法での中心角（＝360°）の大きさは弧の長さ（＝円周）と等しくなります。つまり、
\(360°=2 \pi \)
となります。
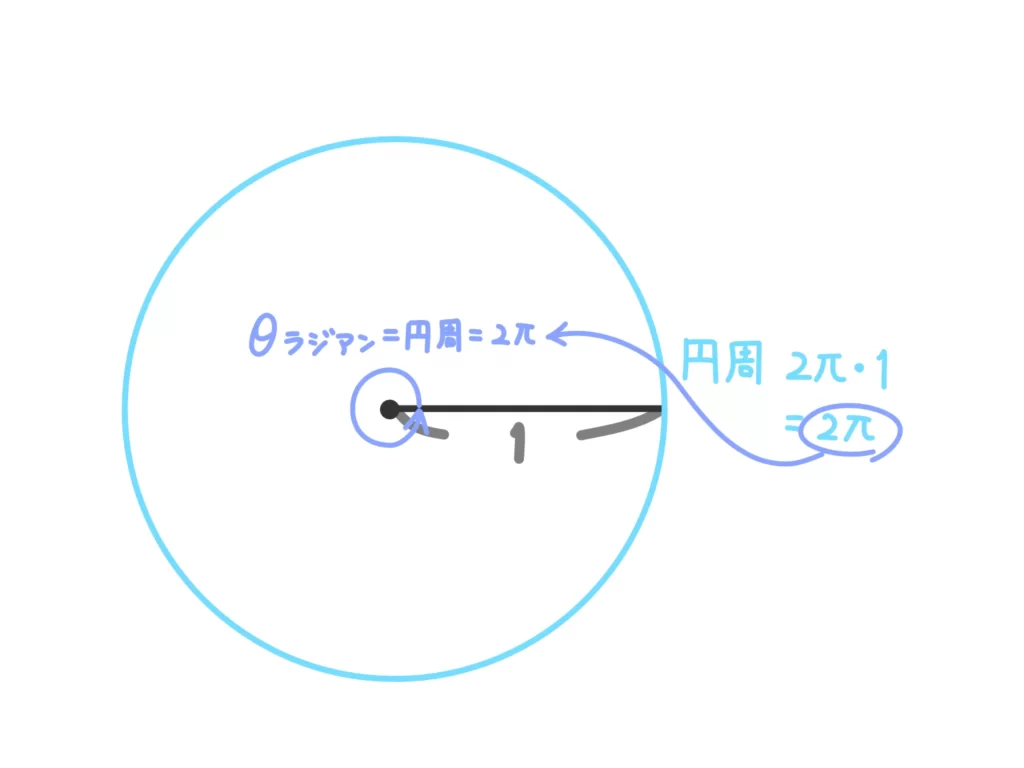
せんせここから、さまざまな有名角の弧度法表記がわかります。
まずは180°が360°の半分なので、180°=\(\pi\)というところから考えていきましょう。
| 度数法 | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
|---|---|---|---|---|---|---|---|---|---|
| 弧度法 | \(0\) | \(\displaystyle \frac{\pi}{6}\) | \(\displaystyle \frac{\pi}{4}\) | \(\displaystyle \frac{\pi}{3}\) | \(\displaystyle \frac{\pi}{2}\) | \(\displaystyle \frac{2}{3}\pi\) | \(\displaystyle \frac{3}{4}\pi\) | \(\displaystyle \frac{5}{6}\pi\) | \(\pi\) |
ちなみに、便宜的に「ラジアン（弧度）」と言っていますが、本質的には比なので単位はありません。
たろぅまた覚えものか…三角関数（比）は覚えることが多くてキライだ…。
と思うかもしれませんが、あとで弧度法を使いこなすコツを述べます。
たろぅコツ！？早く教えて下さい！！
なぜ弧度法の導入が必要なのか？
弧度法を使えば、扇形に関する次の公式が得られます。
扇形の弧・面積を求める公式
中心角\(\theta\)（ただし、\(theta\)は弧度法での角の大きさとする）、半径\(r\)の扇形の弧\(l\)、面積\(S\)とすると、
\(l = r \theta\)
\(\displaystyle S = \frac{1}{2} r^2 \theta = \frac{1}{2}lr\)
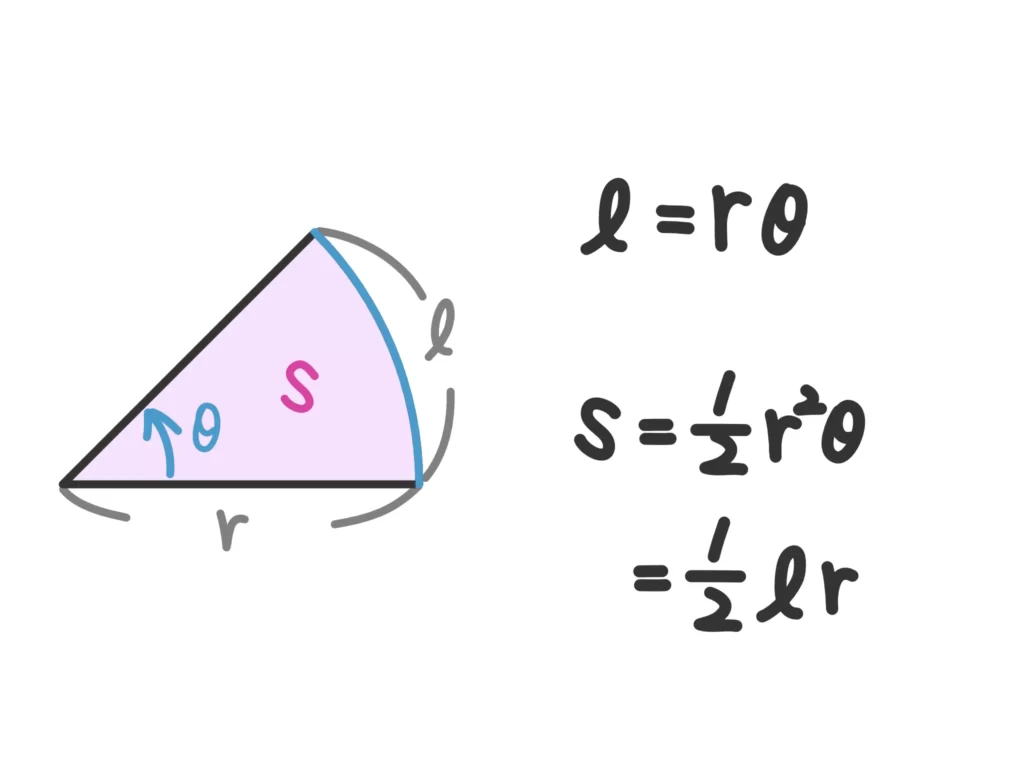
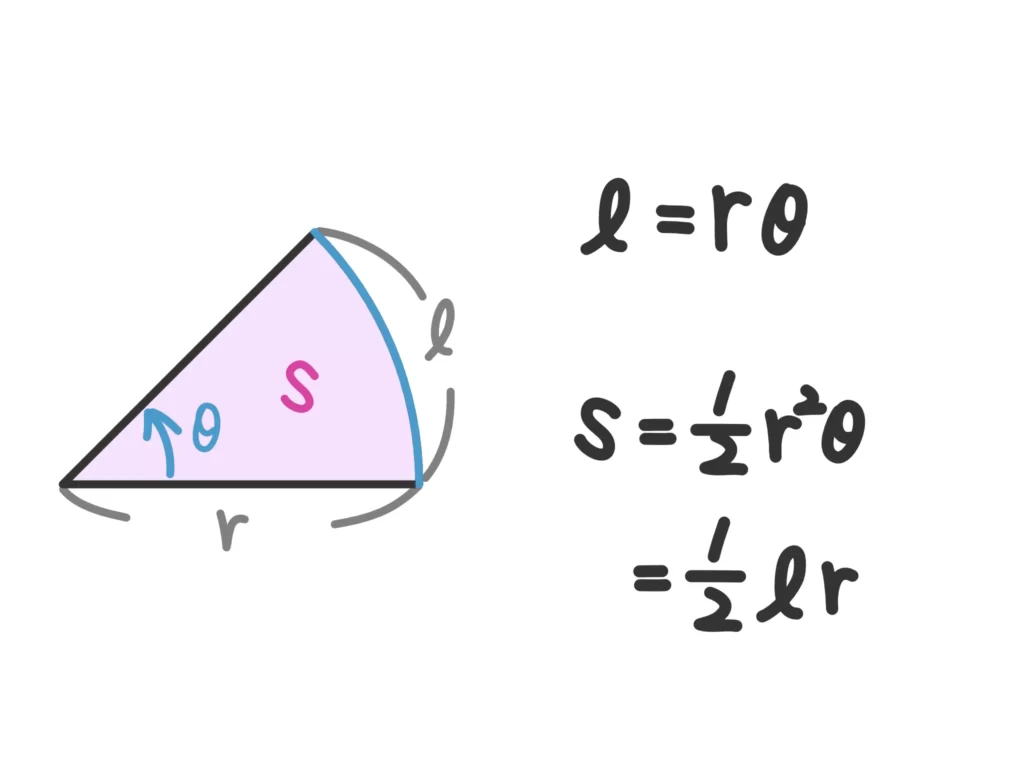
証明はコチラ
（証明）
弧\(l\)は弧度法の定義からすぐに求めることができます。
\(\displaystyle \theta = \frac{l}{r}\)（ラジアン）より
\(l = r \theta\)（終）
扇形の面積は、中心角と面積が比例することを使えば求めることができます。
半径\(r\)の円の面積は\( \pi r^2\)。
これは中心角\(2 \pi\)の扇形の面積といえるので、求める扇型の面積\(S\)、中心角\(\theta\)とすると、
\( S : \theta = \pi r^2 : 2 \pi\)
\( 2 \pi S = \pi r^2 \theta \)
\(\displaystyle S = \frac{1}{2} r^2 \theta\)（終）
また、 \(l = r \theta\)より、
\(\displaystyle S = \frac{1}{2} r^2 \theta\)
\(\displaystyle \quad = \frac{1}{2} r\theta \cdot r = \frac{1}{2}lr\)（終）
まぁこの公式を使える…というのは弧度法の利点でもあるのですが、
たろぅえ…？それだけのために、こんなわけのわかんない弧度法とか導入したの？
と思うかもしれません。
確かに、この公式だけだったらあまり弧度法を導入する意味はないのですが、実際には（あまり教わらない）本質的で重要な導入理由があります。
それは、この後「三角関数」という「関数」を扱っていくからです。
例えば、\(y = \sin{x}\)などですね。このような式を決めると、ある角\(x\)に対してただ一つ\(\sin{x}\)の値が定まるので、関数とみなすことができます。
この、角\(x\)を変数とみなした関数を扱っていくのですが…
角が度数法だとまずい、というのがわかりますよね？
だって、\(x\)軸に単位…ついてますか？
たろぅまぁ…確かに。でもとりあえず単位つけとけばよくないですか？グラフはなんとかかけるんじゃ…。
残念ながら、この後、数学Ⅲではこんな問題が出ます。
例．\( y = \sin{x}\)と\(\displaystyle y=\frac{2}{\pi}x\)（\(\displaystyle 0 \leq x \leq \frac{\pi}{2}\)）で囲まれた部分の面積を求めよ。
たろぅ…。
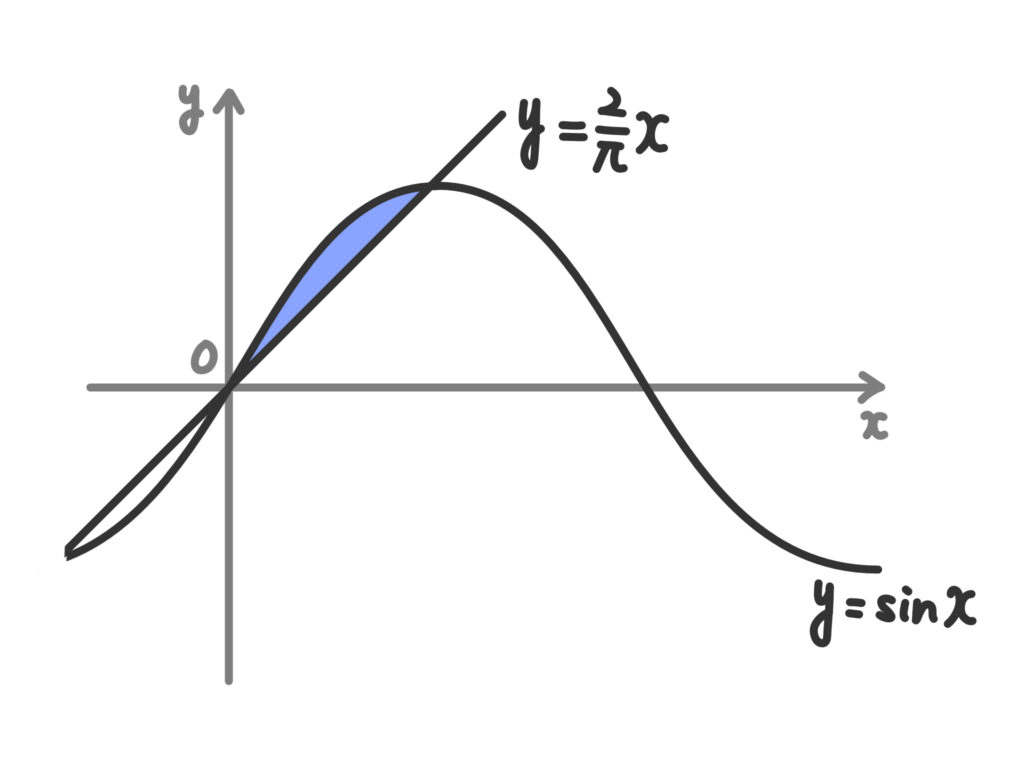
やっぱり、\(x\)の値に単位をつけるのはおかしいですよね？\(\displaystyle y=\frac{2}{\pi}x\)に\(x = 90°\)を代入するって変ですよね。
ということで、三角関数を関数として扱う以上、変数から単位を消しておく＝弧度法を導入しておくことは重要なんです。
弧度法の変換？また覚えるの‥？
先ほど、度数法と弧度法の対応を表にまとめました。
| 度数法 | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
|---|---|---|---|---|---|---|---|---|---|
| 弧度法 | \(0\) | \(\displaystyle \frac{\pi}{6}\) | \(\displaystyle \frac{\pi}{4}\) | \(\displaystyle \frac{\pi}{3}\) | \(\displaystyle \frac{\pi}{2}\) | \(\displaystyle \frac{2}{3}\pi\) | \(\displaystyle \frac{3}{4}\pi\) | \(\displaystyle \frac{5}{6}\pi\) | \(\pi\) |
先生に「これを覚えなさい！」と言われるかもしれませんが、私はこれを覚えなさい、と言ったことはありません。
なぜなら、自分が覚えるのがとても苦手だからです。こんな表…私には覚えるのはムリ。
でも当然、この弧度法を使いこなすことはできます。しかも度数表記と行き来している人より早く、正確に使いこなせます。
英語が話せる人が会話のとき「日本語を考える→英語に訳す」としていないのと一緒です。
ということで、以下では弧度法の覚え方、使い方について説明していきます。
せんせ目指せ弧度法ネイティブ！（←？）
たろぅ…。（早く教えて）
弧度法の使い方
では、私が持っている弧度法のイメージは何かというと…
パイです。
せんせパイです、パイ。アッポーパーイ！ミートゥパーイ！
たろぅ（この人の言うことを信用していいものか…）
先ほどの表で確認しましたが、180°は\(\pi\)です。これが基準になります。パイだけに。
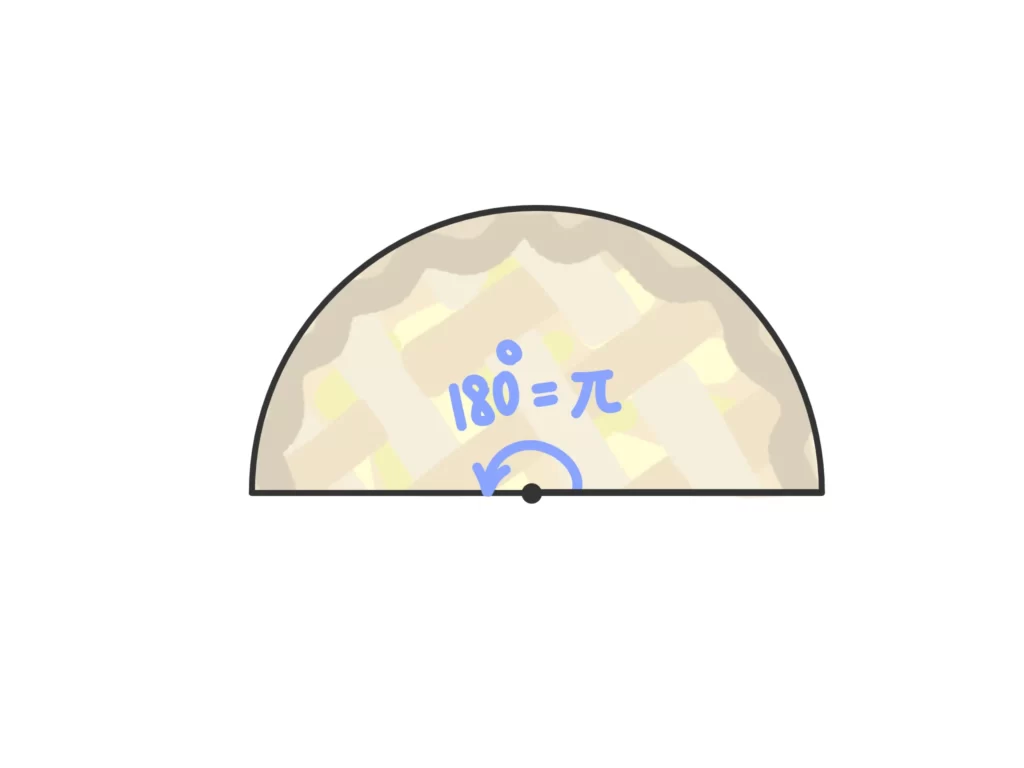
で、これを半分に切ったり、\(\displaystyle \frac{1}{3}\)、\(\displaystyle \frac{1}{4}\)、\(\displaystyle \frac{1}{6}\)に切ったり、するわけですよ。
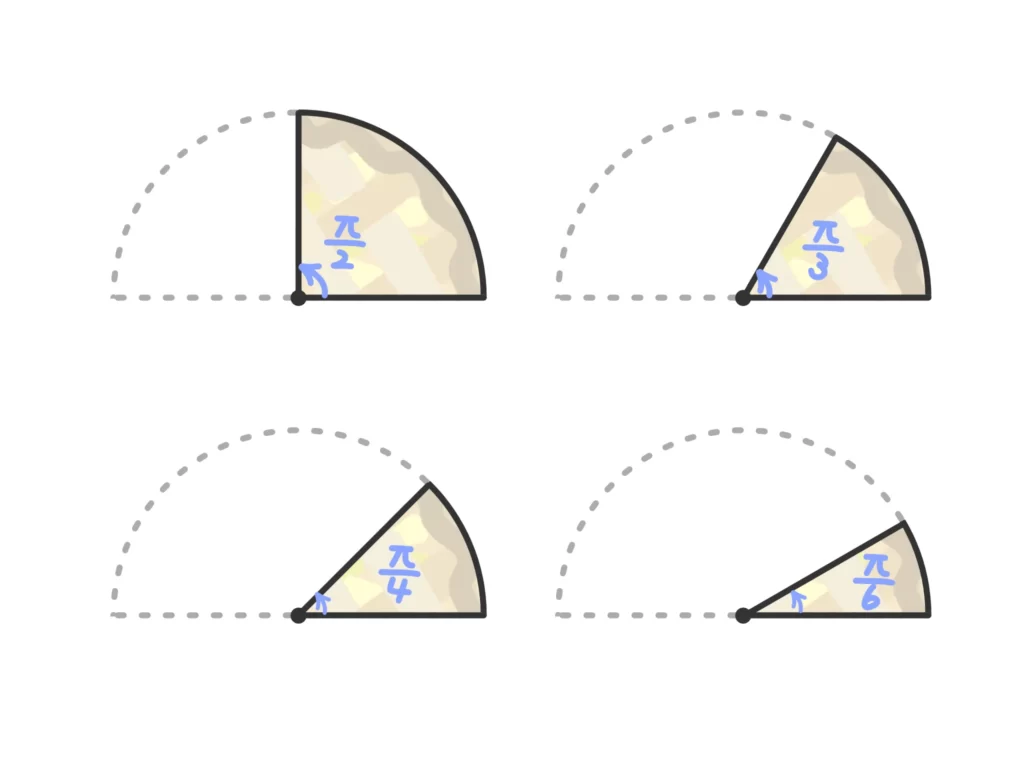
そうすると、\(\displaystyle \frac{\pi}{2}\)、\(\displaystyle \frac{\pi}{3}\)、\(\displaystyle \frac{\pi}{4}\)、\(\displaystyle \frac{\pi}{6}\)が大体これくらいの角だ、というのがビジュアル的にわかります。パイだけに。
せんせこの、何等分したものか？というのをビジュアル的に押さえておきましょう。
弧度法をビジュアル的に捉える利点①「三角関数の値がわかりやすい」
なぜこのように図を使うかというと、弧度法は度数法への変換で話が終わらないからです。十中八九、この弧度法での角を三角関数に入れて、その値を求めます。
例．\(\displaystyle \sin{\frac{5}{6}\pi}\)の値は？
これを
たろぅ\(\displaystyle \frac{5}{6}\pi \cdots = 150°\)でぇ…。えー、\(\displaystyle \sin{150°}\)はぁ…。
とやってたら時間がかかってしまうし、手数の分ミスをする可能性が増えます。
こちらの記事でも説明しましたが、三角関数の値は丸暗記が大変なので、単位円を使ってその都度求める方が楽です。
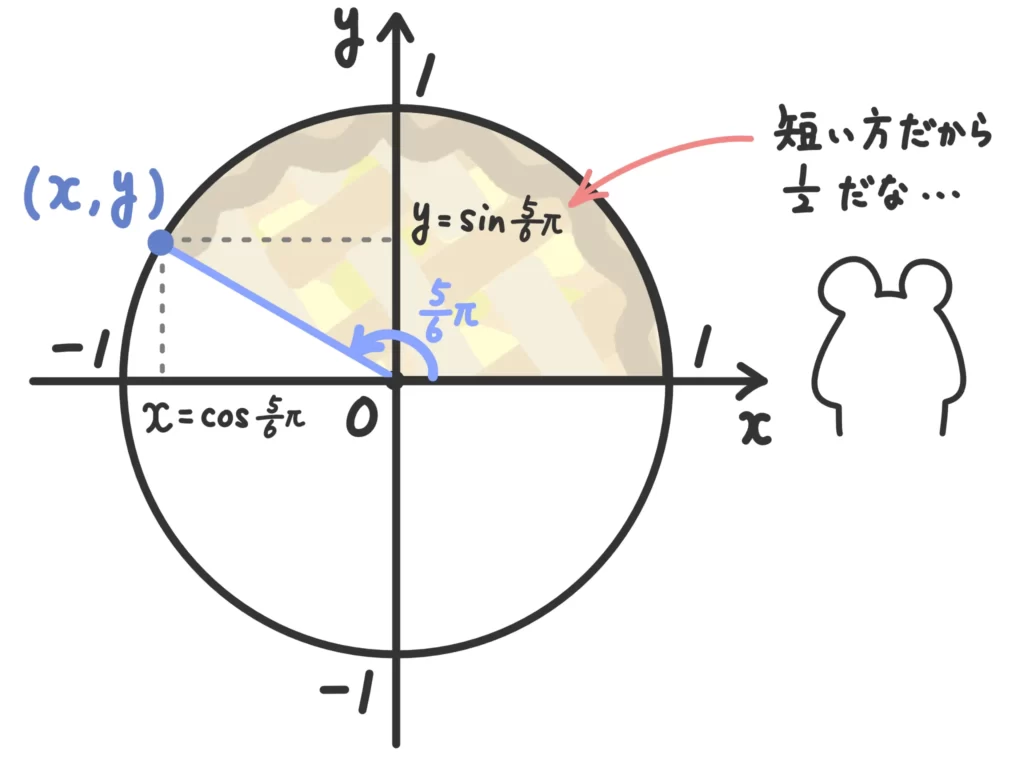
その際に重要なのが「長さ」を意識することですが、この「長さ」とパイを切り分けたイメージがとても親和性が高く、使いやすいんですね。
パイを単位円に乗せてしまえばすぐに三角関数の値を求めることができます。
弧度法をビジュアル的に捉える利点①「弧度法の足し算・引き算がしやすい」
弧度法は、どうしても分数を扱うことになります。
「ー（マイナス）の符号」と「分数」は計算ミスをする要因の大半を占めます（クマの数学日記調べ）。
この後の話になりますが、三角関数は「合成」という手段もあって次のような関数を扱うことが増えます。
例．\(\displaystyle y = \sin{(x+\frac{\pi}{3})}\)
このとき、例えば「\(\displaystyle x = \frac{\pi}{6}\)のときの\(y\)の値が欲しい」とかなったりするんですよ。
こんなときに、
たろぅ\(\displaystyle y = \sin{(\frac{\pi}{6}+\frac{\pi}{3})}\)でぇ…。えー、\(\displaystyle \frac{\pi}{6}+\frac{\pi}{3}\)はぁ…。
とやっていたら時間がかかりますし、計算ミスをする可能性も増えます。
これを「切ったパイを繋げる」と思えば計算がかなり楽です。すぐに「\(\displaystyle \frac{\pi}{2}\)だなぁ」というのが想像できます。
先ほどの\( \displaystyle \frac{5}{6}\pi\)も「\(\pi\)から\( \displaystyle \frac{\pi}{6}\)を切り取ったものだなぁ」ととらえればわかりやすいですよね。
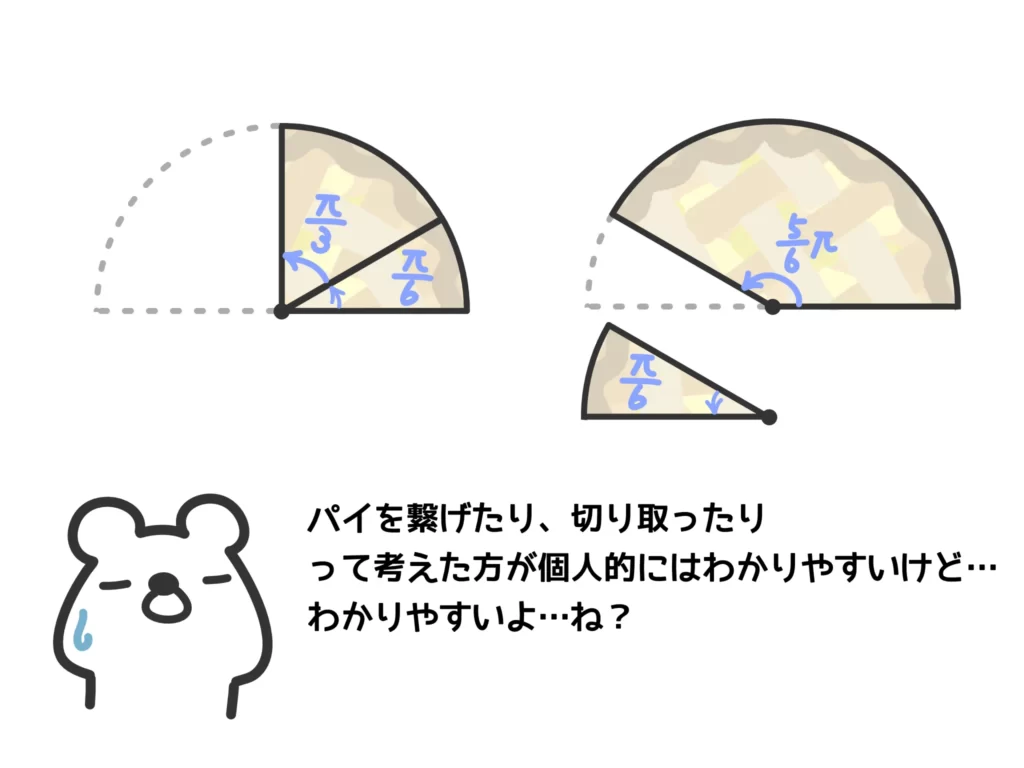
正直この「パイの足し引き」は弧度法に慣れていないとわかりにくい…という側面もありますが、ビジュアル的にイメージできるのは、計算ミスを減らす上でかなり重要です。
弧度法のまとめ
弧度法の基本でした。
特に弧度法を度数法にいちいち直すのはオススメしません。
このあと、ガンガン弧度法を使っていくことになるので、できれば弧度法のイメージのまま扱えるようになってほしいところです。
せんせ目指せ、パイ切りマスター！
ちょっと一息
このブログで活躍してるクマのLINEスタンプもあります！
Youtubeもやってます！数学とは全然関係ない、ゆるいバイク動画です。気晴らしにどうぞ！
