PR
三角関数の合成とは?【合成に必要な三角関数の重要な性質も説明】
三角関数の合成は、加法定理→二倍角(半角)の公式、の後に習います。
ここまでで、三角関数の変形方法の基本は一通り終わるのですが、この三角関数の合成…まぁ色々なやり方(というか教える方の主義主張みたいなのも入り込んで)があって厄介です…。
この記事では①合成の原理とその元になる三角関数の重要な性質、②三角関数の合成方法、③cos合成について説明していきます。
 せんせ
せんせこの記事も多分に私の主義主張が入っています!笑
三角関数の合成とは?



なぜ…なぜこの問題で三角関数が出てくるんだ…?



あら、どうしたの?



いや…この宿題、確か「図形と方程式」の問題だよね?



ん?…あー、確かに「図形と方程式」の問題ね。
問.実数\(x\)、\(y\)が\(x^2 + y^2 = 1\)を満たすとき、\(x + y\)の最大値と最小値を求めよ。



で?何が三角関数なの?



この別解さぁ…
…
(別解)
\(x^2 + y^2 = 1\)より、\(x = \cos{\theta}\)、\(y = \sin{\theta}\)とおくと、
\(x + y = \cos{\theta} + \sin{\theta}\)…



なんでいきなり三角関数が出てくるのぉ…?ていうか、\(x = \cos{\theta}\)とか置いちゃっていいの?
ということで、三角関数の合成です。
上の問題は、「図形と方程式」のいわゆる線形計画法の問題ですが、別解もあります。
そして、その別解は正に三角関数の合成を使うんです。
…が、重要なのは、たろうくんが言うように「なんでいきなり三角関数が出てくるのか?」です。
実はこの\(x\)、\(y\)が三角関数でおける、という事実が合成においても重要なんです。
ちなみに、先程の解答の続き
問.実数\(x\)、\(y\)が\(x^2 + y^2 = 1\)を満たすとき、\(x + y\)の最大値と最小値を求めよ。
(解答)
\(x^2 + y^2 = 1\)より、\(x = \cos{\theta}\)、\(y = \sin{\theta}\)(\( 0 \leq \theta < 2\pi \))とおくと、
\(x + y = \cos{\theta} + \sin{\theta}\)
\(\displaystyle \quad = \sqrt{2} \sin{ \Big( \theta + \frac{\pi}{4} \Big)} \)
\( 0 \leq \theta < 2\pi \)より、
\(\displaystyle -1 \leq \sin{ \Big( \theta + \frac{\pi}{4} \Big)} \leq 1\)
\(\displaystyle -\sqrt{2} \leq \sqrt{2}\sin{ \Big( \theta + \frac{\pi}{4} \Big)} \leq \sqrt{2}\)
よって、最大値は\(\sqrt{2}\)、最小値は\(-\sqrt{2}\)…(答)



三角関数の合成かぁ…そういえば、なんかこの間やった気が…。でもイマイチ使いこなせないんだよね…。



この記事では、三角関数の合成と使い方のコツについて説明していきますよ。



コツぅ!?早く、早く教えて!!
とりあえず、三角関数の合成の公式を載せておきましょう。
三角関数の合成
\(a \sin{\theta} + b \cos{\theta} = \sqrt{a^2+b^2}\sin{( \theta + \alpha )}\)
ただし、\(\alpha \)は\(\displaystyle \cos{\alpha}=\frac{a}{\sqrt{a^2+b^2}}\)、\(\displaystyle \sin{\alpha}=\frac{b}{\sqrt{a^2+b^2}}\)を満たす角。



そういや、こんなの習った気が…。でも、なんでそうなるの?ただし書きも意味わかんないし、全然使いこなせないんだけど…。
…ハイ、ということで丁寧に説明していきましょう。
合成に必要な三角関数の超重要性質
三角関数の合成には2つの重要なポイントがあります。
- 合成の本質は「加法定理」
- 2つの数\(x\)、\(y\)について、
「それぞれを二乗して足すと1になる」
という条件があれば、その\(x\)、\(y\)はそれぞれ\(\cos{\alpha}\)、\(\sin{\alpha}\)と置ける(逆でもOK)
①は教科書や色々なサイトで説明をしていますが、重要な性質は②の方です。
言葉で説明するとわかりにくいですが、要は\(x\)、\(y\)について
\(x^2+y^2=1\)
という条件があれば、\(x = \cos{\alpha}\)、\(y = \sin{\alpha}\)と置くことができる、ということです。



これは単位円を使えばすぐにわかります。\(x\)、\(y\)が\(x^2+y^2=1\)を満たす、ということは点\( (x,y) \)は単位円上にある、ということですから。
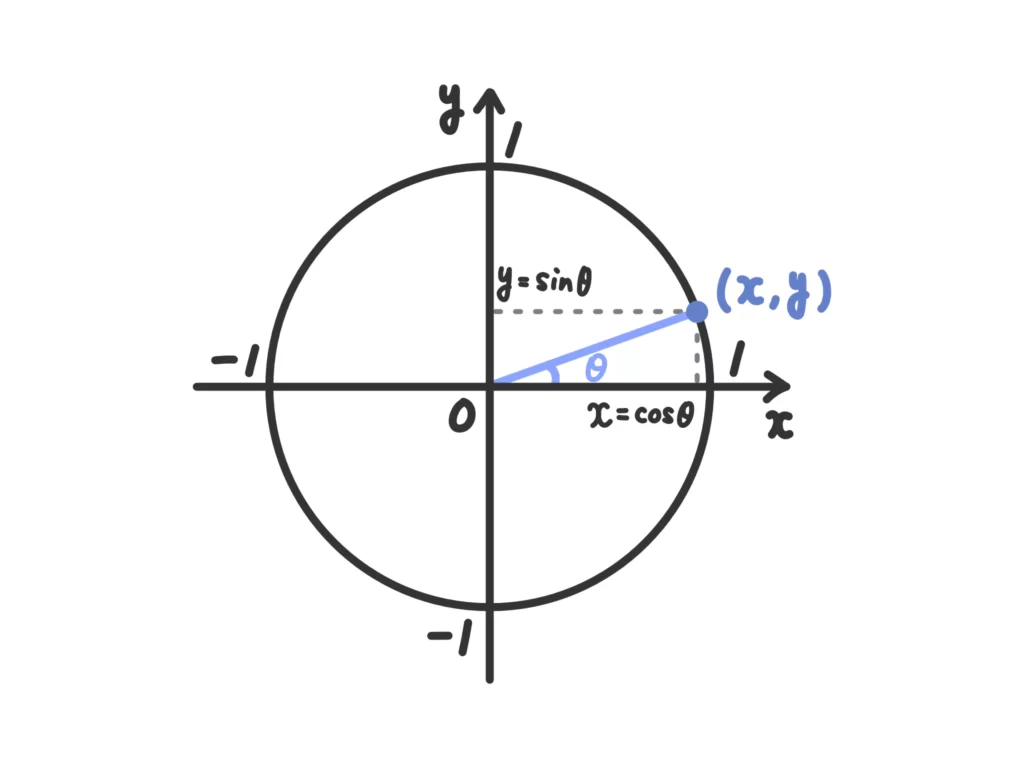

この、「\(x^2+y^2=1\)という条件があれば、三角関数の形で置くことができる」というのはちょっと高度な変数減らしとしても使えます(最初の問題は三角関数を使った変数減らしと言える)が…このあたりはまた別の機会に説明しましょう。
とにかく、「\(x^2+y^2=1\)という条件があれば、三角関数の形で置く」という置き換えはちょくちょく出てきます。
実は今回の合成もこの性質をガッツリ使っています。



それでは少し合成の話を進めていきましょう。
合成は\(a \sin{\theta} + b \cos{\theta}\)の式を、「\(\sin{( \theta + \alpha )}\)」にもっていきたい、という話です。
ここで、加法定理を使って、ゴールである\(\sin{( \theta + \alpha )}\)をバラしてみると、
\(\sin{( \theta + \alpha )} = \sin{\theta}\cos{\alpha}+\cos{\theta}\sin{\alpha}\)
\(\quad = \cos{\alpha}\sin{\theta}+\sin{\alpha}\cos{\theta}\)
となります。
ここで、\(a \sin{\theta} + b \cos{\theta}\)と見比べると、
\(a\)の部分が\(\cos{\alpha}\)
\(b\)の部分が\(\sin{\alpha}\)
になっていることがわかります。
ですが、当然\(a=\cos{\alpha}\)…と置くことはできません。\(\cos{\alpha}\)、\(\sin{\alpha}\)と置くには、それらの文字が「それぞれ二乗して足すと1になる」という条件を満たしていないといけないからです。
…逆にいうと、その条件さえ満たせば\(\cos{\alpha}\)、\(\sin{\alpha}\)と置いていい、ということですよね?
ということで、\(a \sin{\theta} + b \cos{\theta}\)から無理矢理\(\sqrt{a^2+b^2}\)をくくり出します!
すると、
\(\displaystyle a \sin{\theta} + b \cos{\theta} = \sqrt{a^2+b^2} \Big( \frac{a}{\sqrt{a^2+b^2}} \sin{\theta} + \frac{b}{\sqrt{a^2+b^2}} \cos{\theta} \Big) \)
となりますが、ここで\(\displaystyle \frac{a}{\sqrt{a^2+b^2}}\)と\(\displaystyle \frac{b}{\sqrt{a^2+b^2}}\)について考えます。
この2つの式はまさに「それぞれ二乗して足すと1になります」よね?
\(\displaystyle \Big( \frac{a}{\sqrt{a^2+b^2}} \Big)^2 + \Big( \frac{b}{\sqrt{a^2+b^2}} \Big)^2 = \frac{a^2+b^2}{a^2+b^2} = 1\)
丁寧に説明して長くなってしまいましたが、これで、
\(\displaystyle \frac{a}{\sqrt{a^2+b^2}} = \cos{\alpha}\)、\(\displaystyle \frac{b}{\sqrt{a^2+b^2}} = \sin{\alpha}\)
と置くことができ、\(a \sin{\theta} + b \cos{\theta} = \sqrt{a^2+b^2}\sin{( \theta + \alpha )}\)となります。
問.\(\displaystyle \tan{\theta} = \frac{4}{3} \)のとき、\(\sin{\theta}\)、\(\cos{\theta}\)の値をそれぞれ求めよ。ただし、\( 0 \leq \theta \leq \pi \)とする。
答え
\(\displaystyle \sin{\theta} = \frac{4}{5}\)、\(\displaystyle \cos{\theta} = \frac{3}{5}\)
三角関数の合成方法



ちょっと話が長くなったので、三角関数の合成方法についてまとめておきます。さっきの話も最後が雑でしたし…。
本質的な合成方法
本質的な合成方法をするには、
- 毎回\(\sqrt{a^2+b^2}\)でくくる。
- \(\displaystyle \frac{a}{\sqrt{a^2+b^2}}\)と\(\displaystyle \frac{b}{\sqrt{a^2+b^2}}\)を\(\cos{\alpha}\)、\(\sin{\alpha}\)と置いていい。(実は、どちらを\(\cos{\alpha}\)、\(\sin{\alpha}\)としてもいい。)
- 最終的に加法定理を使う。
の3つを覚えておかなければいけません。
特に②ですね。この「本質的な合成」を推奨する人も多いのですが、理由は「cos合成にも対応できるから」です。その「cos合成」をするためにも②の性質を押さえておく必要があります。
でもまぁ…「cos合成」ってほとんど出ないんですよね(たしか過去、センター試験と共通テストで1度ずつ出題されたことがあるはず)。共通テストのような「解答欄に合わせていく」という形式じゃないと「cos合成」をする意味はありませんし、あまり問題を解く上で本質的ではない気もします(sinとcosは位相がずれてるだけ…なので)。
「cos合成」にとらわれずに、どちらかというと、②の性質をちゃんと理解することが重要だと思います。



とはいえ、「cos合成出たらどうすんの?」というのは確かに一理あります。
とりあえず②(→③の流れ)が理解できれば、自然と「cos合成」もできるようになります。
三角関数の合成方法(本質的な方法)
\(\displaystyle a \sin{\theta} + b \cos{\theta} = \sqrt{a^2+b^2} \Big( \frac{a}{\sqrt{a^2+b^2}} \sin{\theta} + \frac{b}{\sqrt{a^2+b^2}} \cos{\theta} \Big) \)
ここで、\(\displaystyle \frac{a}{\sqrt{a^2+b^2}} = \cos{\alpha}\)、\(\displaystyle \frac{b}{\sqrt{a^2+b^2}} = \sin{\alpha}\)とすると、
\( a \sin{\theta} + b \cos{\theta} = \sqrt{a^2+b^2} ( \cos{\alpha} \sin{\theta} + \sin{\alpha} \cos{\theta} ) \)
\( \quad = \sqrt{a^2+b^2} ( \sin{\theta} \cos{\alpha}+ \cos{\theta} \sin{\alpha} ) \)
\( \quad = \sqrt{a^2+b^2} \sin{ ( \theta + \alpha) } \)
例.\( \sqrt{3} \sin{\theta} + \cos{\theta} \) を\(k \sin{(\theta+\alpha)}\)の形に変形せよ。
(解答)
\(\displaystyle \sqrt{3} \sin{\theta} + \cos{\theta} = \sqrt{3 + 1} \Big( \frac{\sqrt{3}}{\sqrt{3 + 1}}\sin{\theta} + \frac{1}{\sqrt{3 + 1}}\cos{\theta} \Big) \)
\(\displaystyle \quad = 2 \Big( \frac{\sqrt{3}}{2} \sin{\theta} + \frac{1}{2} \cos{\theta} \Big) \)
ここで、\(\displaystyle \frac{\sqrt{3}}{2} = \cos{\frac{\pi}{6}}\)、\(\displaystyle \frac{1}{2} = \sin{\frac{\pi}{6}}\)とおけるので、
\(\displaystyle \sqrt{3} \sin{\theta} + \cos{\theta} = 2 \Big( \sin{\theta}\cos{\frac{\pi}{6}} + \cos{\theta} \sin{\frac{\pi}{6}} \Big) \)
よって、\(\displaystyle \sqrt{3} \sin{\theta} + \cos{\theta} = 2 \sin{ \Big( \theta + \frac{\pi}{6} \Big) }\)…(答)
実践的な合成方法
ただ、本質的な合成方法は、どうしても変形しにくい部分があります。それは、
ここで、\(\displaystyle \frac{\sqrt{3}}{2} = \cos{\frac{\pi}{6}}\)、\(\displaystyle \frac{1}{2} = \sin{\frac{\pi}{6}}\)とおけるので、
この部分ですね。



この角度を決定するのがちょっとわかりにくいんです…。
なので、実践的には図を使って合成する方が早くて確実です。
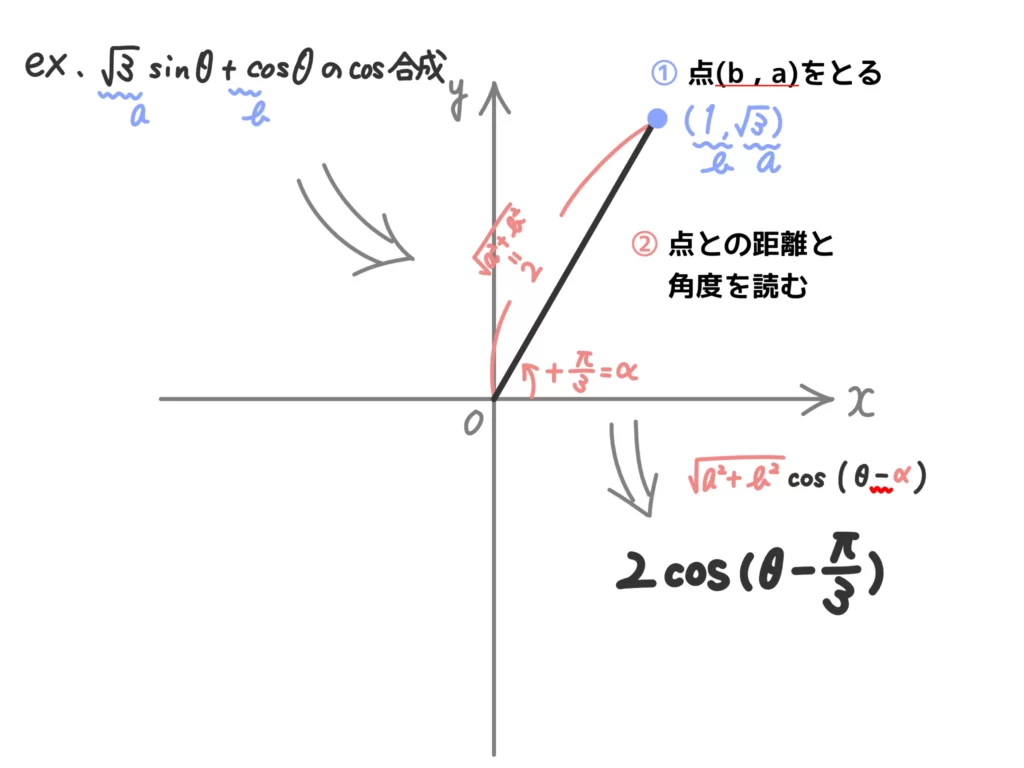
例.\( \sqrt{3} \sin{\theta} + \cos{\theta} \) を\(k \sin{(\theta+\alpha)}\)の形に変形せよ。



次のような図を使って合成します!
(解答)
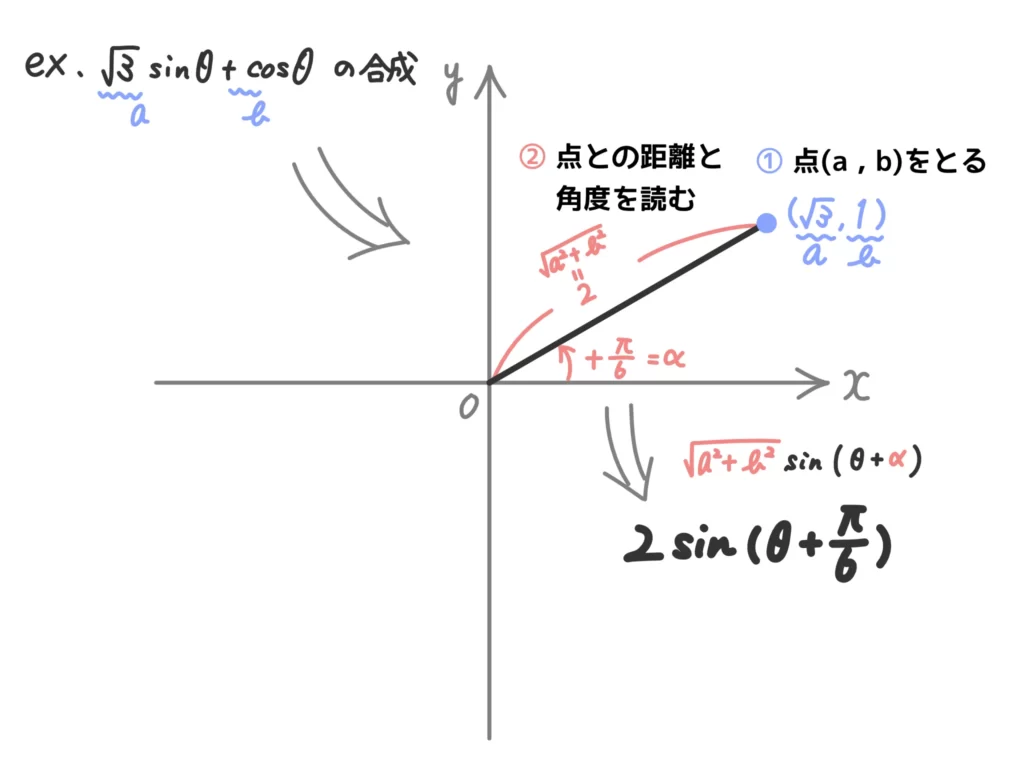

よって、\(\displaystyle \sqrt{3} \sin{\theta} + \cos{\theta} = 2 \sin{ \Big( \theta + \frac{\pi}{6} \Big) }\)…(答)
なぜこの図で合成ができるのか?
角を読む際のポイントは、
\(\displaystyle \cos{\alpha}=\frac{a}{\sqrt{a^2+b^2}}\)、\(\displaystyle \sin{\alpha}=\frac{b}{\sqrt{a^2+b^2}}\)
を満たす\(\alpha\)を見つけることです。
点\( (a , b) \)をとって\(x\)軸正の方向と成す角を読むことで、自然と
\(\displaystyle \cos{\alpha}=\frac{a}{\sqrt{a^2+b^2}}\)、\(\displaystyle \sin{\alpha}=\frac{b}{\sqrt{a^2+b^2}}\)
となるからです。
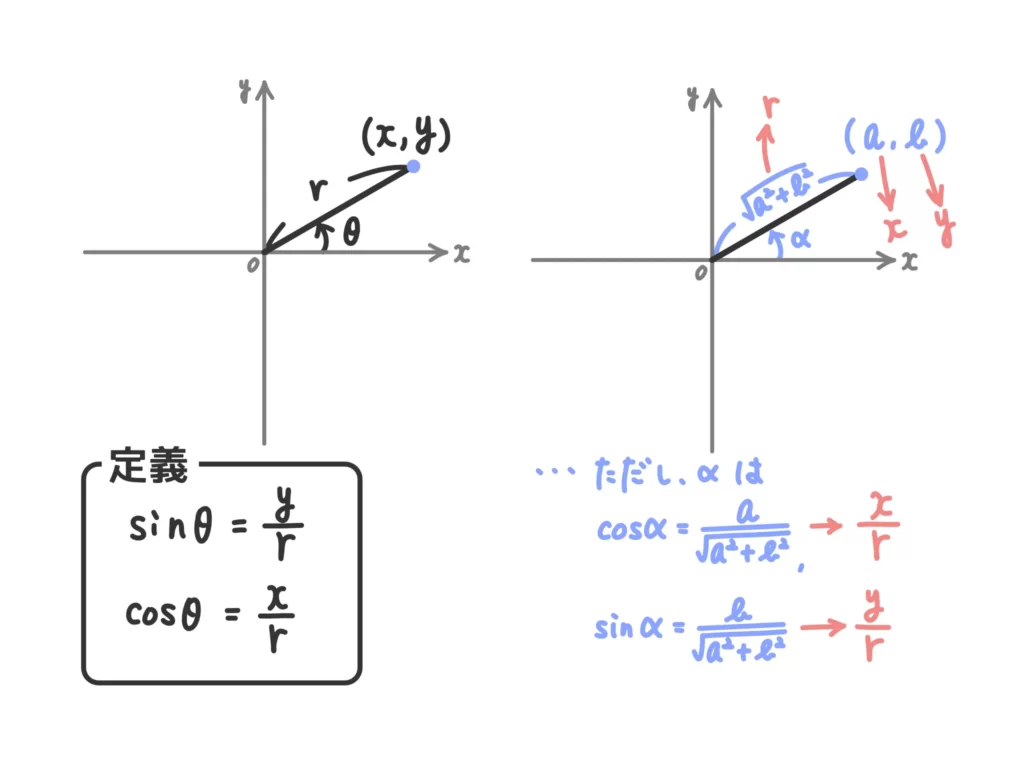

加えて、原点と点\( (a , b) \)との距離が合成に必要な\(\sqrt{a^2 + b^2}\)となります。
おまけ.三角関数のcos合成
ついでに、といってはなんですが、cos合成も説明しておきます。
\(\displaystyle a \sin{\theta} + b \cos{\theta} = \sqrt{a^2+b^2} \Big( \frac{a}{\sqrt{a^2+b^2}} \sin{\theta} + \frac{b}{\sqrt{a^2+b^2}} \cos{\theta} \Big) \)
cos合成はこのあとがポイントです。
\(\displaystyle \frac{a}{\sqrt{a^2+b^2}} = \sin{\alpha}\)、\(\displaystyle \frac{b}{\sqrt{a^2+b^2}} = \cos{\alpha}\)と置くことが重要です。



「どちらを\(\cos{\alpha}\)、\(\sin{\alpha}\)としてもいい。」というところがポイントですね。
そうすると、
\(\displaystyle a \sin{\theta} + b \cos{\theta} = \sqrt{a^2+b^2} ( \sin{\alpha} \sin{\theta} + \cos{\alpha} \cos{\theta} ) \)
\(\quad = \sqrt{a^2+b^2} (\cos{\theta}\cos{\alpha} + \sin{\theta}\sin{\alpha} ) \)
\(\quad = \sqrt{a^2+b^2} \cos{ ( \theta – \alpha ) } \)
となります。これでcos合成の完成です。
このcos合成の場合は、角度が\(\theta – \alpha\)となります。これは、そもそも合成は加法定理を使っているからです。



\( \cos{ ( \theta – \alpha ) }=\cos{\theta}\cos{\alpha} + \sin{\theta}\sin{\alpha} \)ですからね。
例’.\( \sqrt{3} \sin{\theta} + \cos{\theta} \) を\(k \cos{(\theta-\alpha)}\)の形に変形せよ。
(解答)
\(\displaystyle \sqrt{3} \sin{\theta} + \cos{\theta} = 2 \Big( \frac{\sqrt{3}}{2} \sin{\theta} + \frac{1}{2} \cos{\theta} \Big) \)
ここで、\(\displaystyle \frac{\sqrt{3}}{2} = \sin{\frac{\pi}{3}}\)、\(\displaystyle \frac{1}{2} = \cos{\frac{\pi}{3}}\)とおけるので、
\(\displaystyle \sqrt{3} \sin{\theta} + \cos{\theta} = 2 \Big( \cos{\theta}\cos{\frac{\pi}{3}} + \cos{\theta} \cos{\frac{\pi}{3}} \Big) \)
よって、\(\displaystyle \sqrt{3} \sin{\theta} + \cos{\theta} = 2 \cos{ \Big( \theta – \frac{\pi}{3} \Big) }\)…(答)
ちなみに、cosの形にしたいだけであれば、sinから無理矢理変形することもできます。



\(\displaystyle \sin{ \Big( □ + \frac{\pi}{2} \Big) } = \cos{□} \)となる性質を使えばOKです。
例’.\( \sqrt{3} \sin{\theta} + \cos{\theta} \) を\(k \cos{(\theta-\alpha)}\)の形に変形せよ。
(解答)
\(\displaystyle \sqrt{3} \sin{\theta} + \cos{\theta} = \cdots = 2 \sin{ \Big( \theta + \frac{\pi}{6} \Big) }\)
ここで、\(\displaystyle \theta + \frac{\pi}{6} = □ + \frac{\pi}{2} \)とおくと、
\(\displaystyle □ = \theta – \frac{\pi}{3}\)
よって、
\(\displaystyle 2 \sin{ \Big( \theta + \frac{\pi}{6} \Big) } = 2 \sin{ \Big( \theta – \frac{\pi}{3} + \frac{\pi}{2} \Big) } = 2 \cos{ \Big( \theta – \frac{\pi}{3} \Big) }\)…(答)



ま…この手は具体的な角度が求められるようなときにしか使えませんけどね。
sin合成のときのように図を使ってできなくもない…ですが、①点を\( (b , a)\)ととらないといけないこと、②読んだ角を引くこと、の2点に注意しなければいけないので、それなら「本質的な合成」でcos合成した方がいい気がします。
(解答)

よって、\(\displaystyle \sqrt{3} \sin{\theta} + \cos{\theta} = 2 \cos{ \Big( \theta – \frac{\pi}{3} \Big) }\)…(答)
問.\(\theta\)の関数\( y = \sin{\theta} + p \cos{\theta}\)の最大値を次の問にしたがって求めよ。ただし、\(p > 0\)、\(\displaystyle 0 \leq \theta \leq \frac{\pi}{2}\)とする。
(1) \(y\)を\(y = k \sin{(\theta + A)}\)の形に変形したとき、\(k\)の値と、\(\sin{A}\)、\(\cos{A}\)の値を求めよ。ただし、\(\displaystyle 0 < A < \frac{\pi}{2}\)とする。
(2) \(y\)の最大値を求めよ。また、そのときの\(\theta\)を\(A\)を用いて表せ。
(3) \(y\)を\(y = l \cos{(\theta – \alpha)}\)の形に変形したとき、\(l\)の値と、\(\sin{\alpha}\)、\(\cos{\alpha}\)の値を求めよ。ただし、\(\displaystyle 0 < \alpha < \frac{\pi}{2}\)とする。
(4) (3)の式を用いて\(y\)の最大値と、そのときの\(\theta\)を\(\alpha\)を用いて表せ。また、\(y\)が最大となるときの\(\alpha\)を\(A\)を用いて表せ。
答え
(1) \(k = \sqrt{1 + p^2}\)、\(\displaystyle \sin{A}=\frac{p}{\sqrt{1+p^2}}\)、\(\displaystyle \cos{A}=\frac{1}{\sqrt{1+p^2}}\)
(2) 最大値\( \sqrt{1 + p^2} \)、\(\displaystyle \theta = \frac{\pi}{2} – A\)
(3) \(l = \sqrt{1 + p^2}\)、\(\displaystyle \sin{\alpha}=\frac{1}{\sqrt{1+p^2}}\)、\(\displaystyle \cos{\alpha}=\frac{p}{\sqrt{1+p^2}}\)
(4) 最大値\( \sqrt{1 + p^2} \)、\(\displaystyle \theta = \alpha\)、\(\displaystyle \alpha = \frac{\pi}{2} – A\)
三角関数の合成のまとめ
三角関数の合成のまとめでした。
- とりあえず図を使って三角関数の合成(sin合成)ができるようになる。
- 「それぞれ二乗して足すと1になる変数は\(\sin{\theta}\)と\(\cos{\theta}\)とおける」というポイントを押さえて、cos合成ができるようになる。
これらができれば大丈夫です。