二次関数に絶対値がついてる！【絶対値の外し方とグラフのかき方】

2024年1月30日2024年4月29日

絶対値…苦手な生徒が多いですが、関数に絶対値がついているとなおさら難しく感じます。

ですが、絶対値がついた関数もコツを掴めば簡単にかくことができます。

この記事では一次関数（直線）、二次関数（放物線）を中心に絶対値がついた関数の処理方法を説明していきます。

絶対値がついた関数

たろぅ

けっ！こんな問題よぅ、やってられるかよ！

はなこ

あら、なんかずいぶん尖ってるわね。

たろぅ

こんなよぅ！「絶対値がついた関数のグラフをかけ」だぁ！？これが尖らずにいられるか！誰か教えてください！

はなこ

尖って…るのかな？

ということで「絶対値がついた関数のグラフ」です。

絶対値がついた関数のグラフは、絶対値の特性上、強制的に上下（\(y\)方向）を反転させられる部分がでてくるので、自然と尖った部分が出てきます。

せんせ

この記事では絶対値の性質を押さえながら、一次関数（直線）や二次関数（放物線）をメインに「絶対値がついた関数のグラフ」のかき方のコツを勉強していきましょう！

絶対値がついた一次関数

先に、絶対値の性質の重要なポイントを押さえておきます。

それは、

絶対値の中身が＋（プラス）だったらそのまま、絶対値の中身がー（マイナス）だったらー（マイナス）を付けて反転・強制的に＋（プラス）にする。

という点です。

これは絶対値の性質そのものなのですが、中身がー（マイナス）だったら強制的に反転して＋（プラス）にする、という意識をもっていれば、実は絶対値のついた関数のグラフがかきやすいです。

せんせ

絶対値のついた一次関数の例をいくつかあげながら、グラフをかく感覚を押さえていきましょう！

例1．関数\(y=|x-2|\)のグラフをかけ。

このタイプの「全体に絶対値がついている」関数のグラフは比較的簡単です。

先ほどの中身がー（マイナス）だったら強制的に反転して＋（プラス）にする、という絶対値の感覚を押さえていればすぐにかけます。

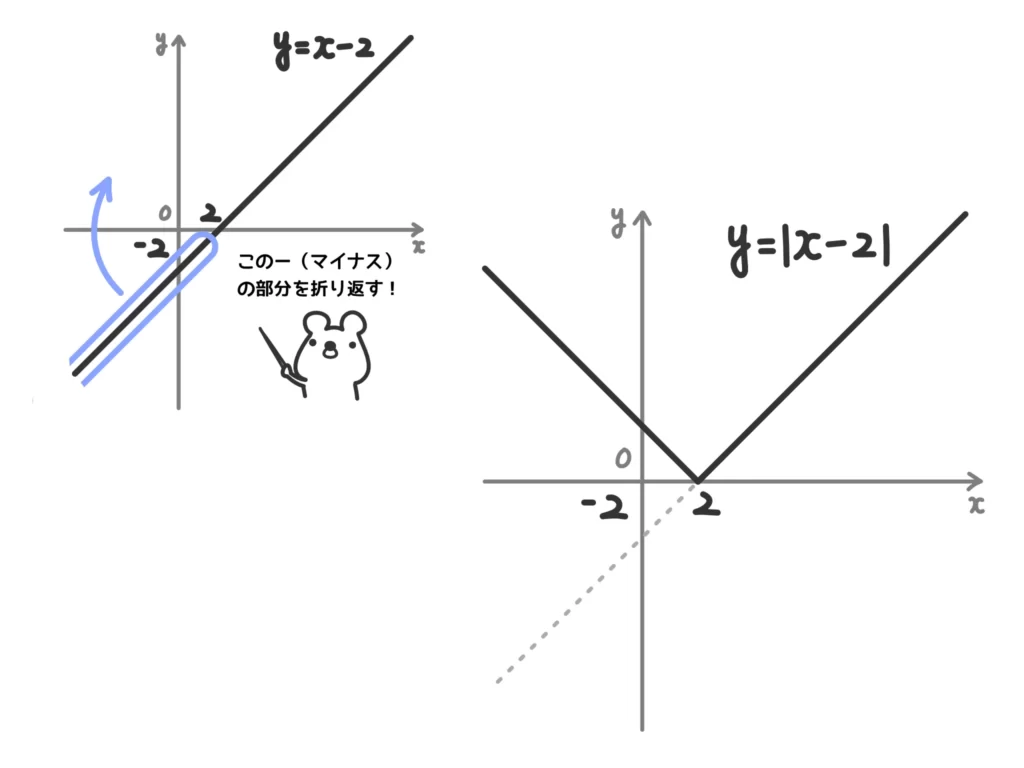
つまり、中身のグラフをかいたときに（中身＝\(y\)の値が）ー（マイナス）になっている部分、要は\(x\)軸より下の部分を折り返せばOKです。

せんせ

もちろん丁寧に場合分けをしてグラフをかいてもよいですが、そこまで一生懸命になってかくほどでもないかな…と思います。問題のレベルが上がると、絶対値がついた関数のグラフをかくのは問題のほんの一部であることも多いからです。

（解答）
\(y=|x-2|\)のグラフは次のようになる。

例2．関数\(y = |x| + 1\)のグラフをかけ。

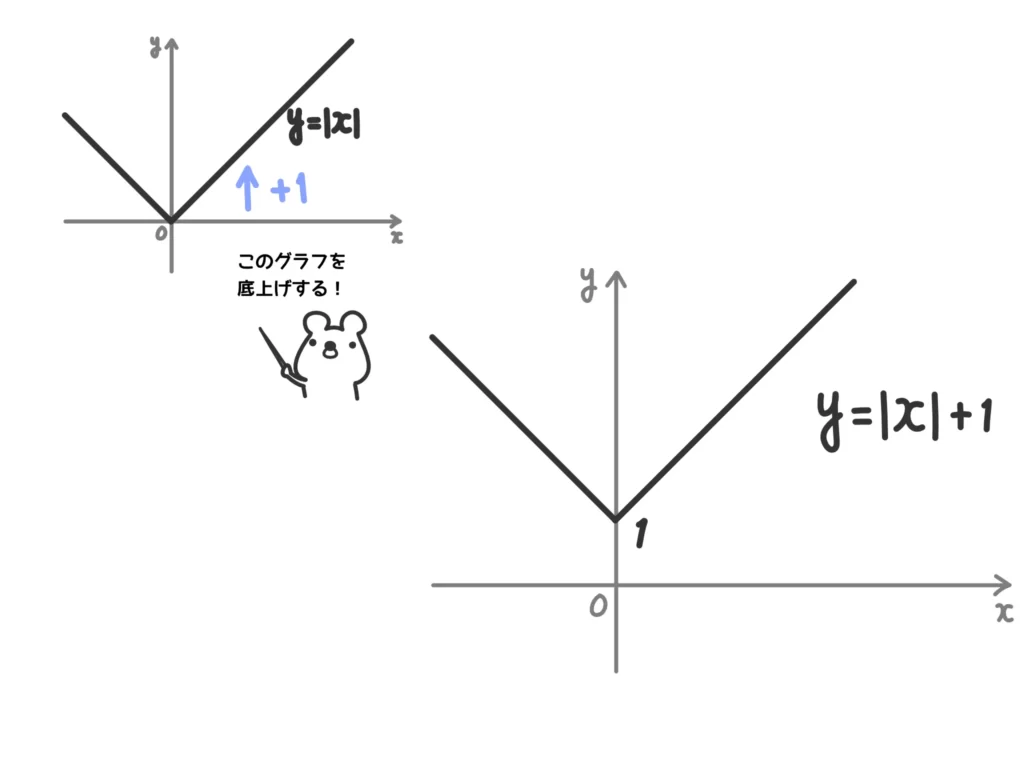
絶対値の中身による場合分けをしてもいいですが、「\(y=|x|\)に\(+1\)（＝\(y\)軸正の方向に１平行移動する）」という感覚でもOKです。

せんせ

この「定数部分」はそれ以外の部分でできたグラフの底上げ（下げ）、というイメージです。これは他のグラフでも使える感覚なので知っておいて損はないです。

（解答）
\(y = |x| + 1\)のグラフは次のようになる。

絶対値がついた二次関数

さて、この記事のメインですね。

絶対値がついた二次関数のグラフは、数学IIの積分の分野でもよく出てくるので、サクッとかけた方がいいですね。

せんせ

とはいえ、ここから場合分けが必要なケースも出てきます。場合分け以外の部分で手間取らないように、平方完成はサッとできるようにしておいてください。

結論を先に言っておきますが、基本的には場合分けです。が、関数全体に絶対値がついている場合は、先程の「絶対値の感覚」を使ってかくこともできます。

ケース１．絶対値が全体についているグラフ

これは一次関数のときと一緒で、中身のグラフをかいたときにー（マイナス）になっている部分、要は\(x\)軸より下の部分を折り返せばOKです。

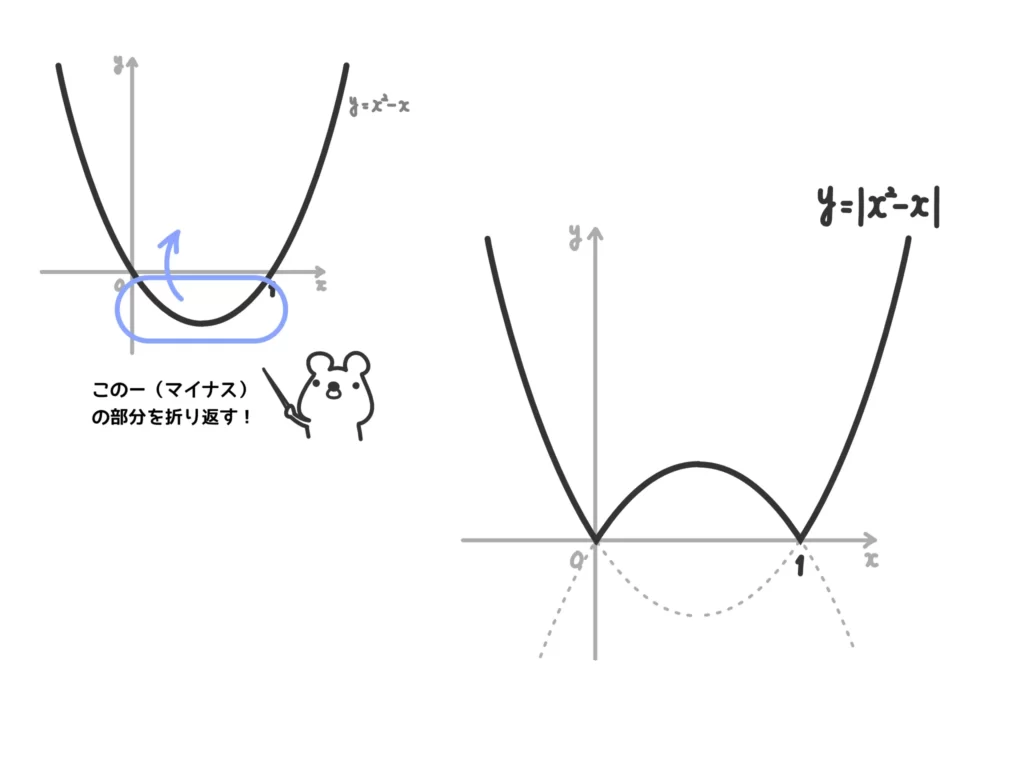
例3．関数\(y = |x^2-x | \)のグラフをかけ。

一次関数の全体に絶対値がついているときの感覚と同じです。

要は「\(y\)がー（マイナス）の部分＝\(x\)軸より下に出ている部分を折り返せばよい」というかき方でかくことができます。

中身が二次関数なので、下に出ている部分を求めるためには二次不等式を解かなければいけません…。が、実際には二次方程式を解くだけでも十分です。

せんせ

なぜならば、下に凸だろうが上に凸だろうが、結局\(x\)軸との交点を基準に\(x\)軸の上に折り返すからです。（だから、基本的に\(x^2\)の係数がー（マイナス）になるような絶対値がついたグラフの問題はないですね…本質的に無駄ですから。）

（真面目な解答）

(i) \( x^2-x \geq 0\)、つまり\(x \leq 0, 1 \leq x\)のとき

　\(y=x^2-x\)

(ii) \( x^2-x < 0\)、つまり\( 0 < x < 1 \)のとき

　\(y=-x^2+x\)

(i)、(ii)より、グラフは次のようになる。

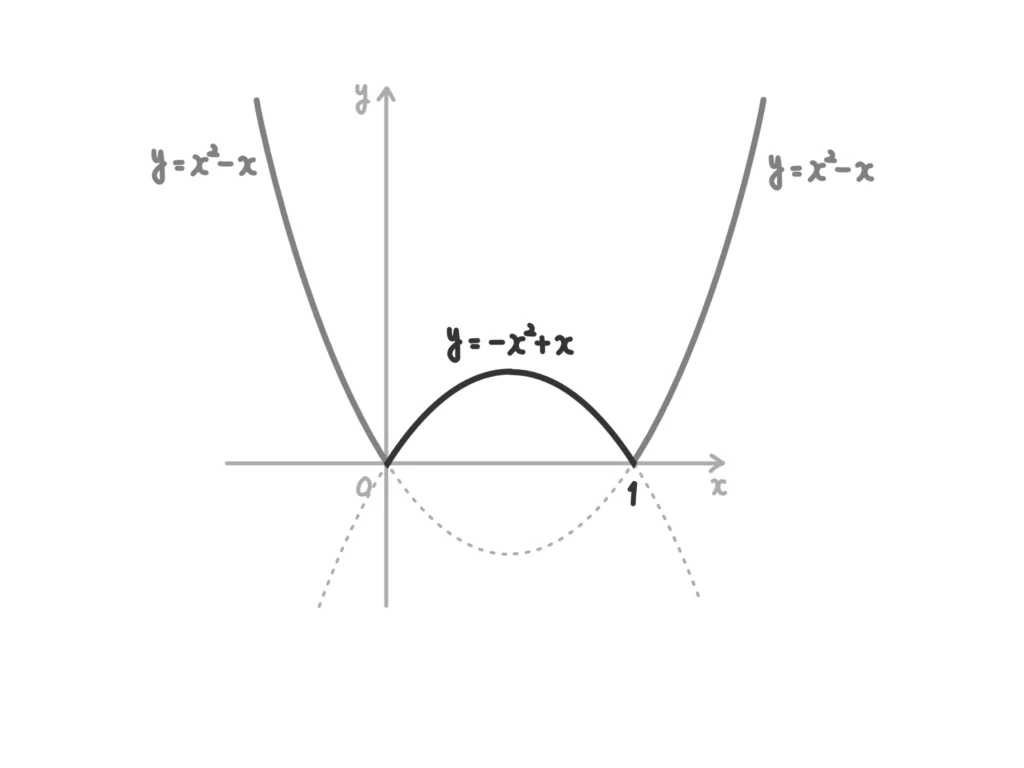
（簡単な解答…というか、かき方）

\(y = |x^2-x|\)のグラフは次のようになる。

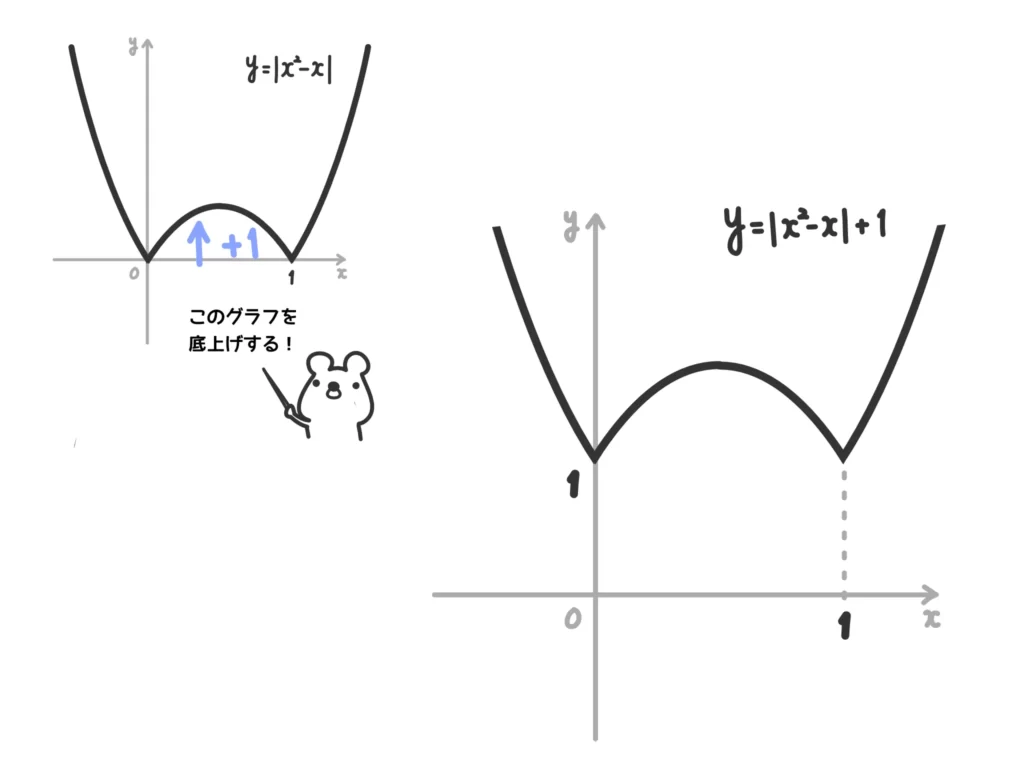
例4．関数\(y = | x^2-x| + 1 \)のグラフをかけ。

これもグラフの感覚でいうと、\(y = |x^2-x|\)のグラフを\(y\)軸方向に\(+1\)すればいい、という感じですね。

（解答）

\(y = | x^2-x| + 1 \)のグラフは次のようになる。

ケース２．絶対値がx一次の項についているグラフ

\(x\)一次の項に絶対値がついているケースは、残念ながら場合分けをするしかないです…。

せんせ

丁寧に場合分けしていきましょう。

例5．関数\( y = x^2 -4|x-1| \)のグラフをかけ。

絶対値は中身の＋（プラス）ー（マイナス）による場合分けをします。

せんせ

こちらでも説明しましたが、\(x\)の＋（プラス）ー（マイナス）ではありません！あくまで中身です！中身！

（解答）

(i) \( x – 1 < 0\)、つまり\(x < 1\)のとき

　\( y = x^2 +4(x-1) \)
　\(\quad = x^2 +4x -4\)
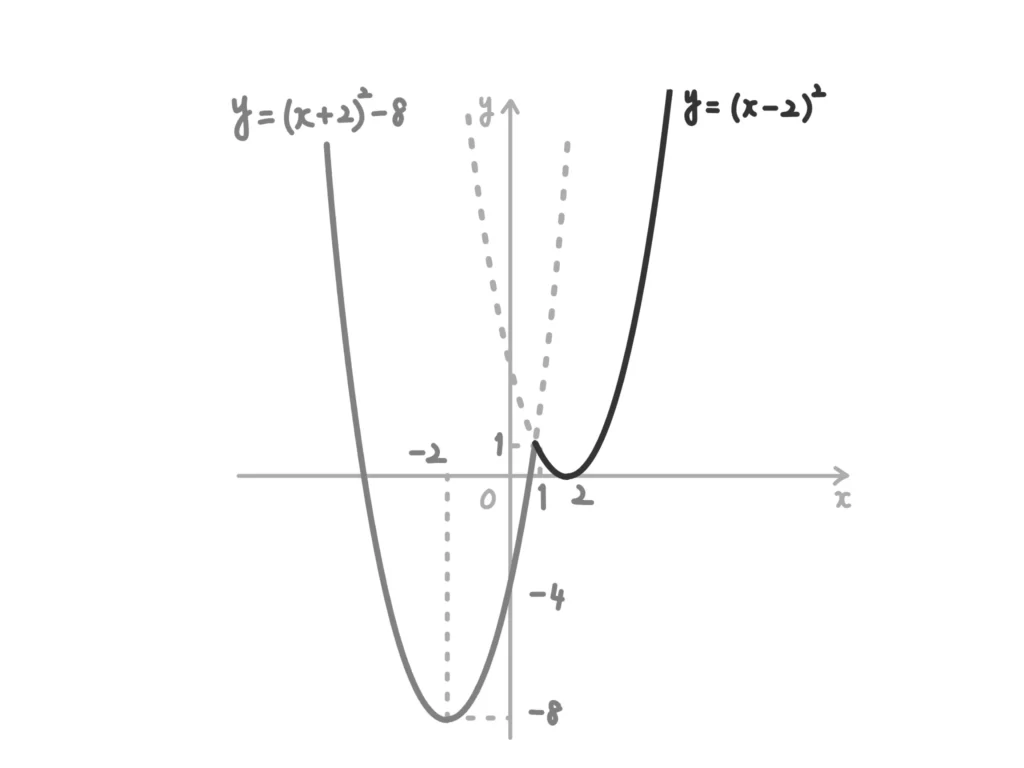
　\(y = (x +2)^2 -8\)

(ii) \( x – 1 \geq 0\)、つまり\(1 \leq x\)のとき

　\( y = x^2 -4(x-1) \)
　\(\quad = x^2 -4x +4\)
　\(y = (x -2)^2\)

(i)、(ii)より、グラフは次のようになる。

応用編．絶対値が２ヶ所についた二次関数のグラフ

応用編ですが、絶対値が２ヶ所ついたグラフもあります。

（絶対値の中身が\(x\)の一次式）×２ヶ所…は、たまにありますが、次の練習問題2-5のように（中身が\(x\)の二次式）＋（中身が\(x\)の一次式）というのはあまり見ませんね。

せんせ

一応練習問題も準備しましたが…ここまでの問題はあまり出ないので、まずは上記の、１ヶ所に絶対値がついたグラフがかけるようにしておきましょう。
「ちょっと骨のある問題が解きたい！」という人はぜひチャレンジしてみてください。

練習問題1-5【No.13】

問．次の各問いに答えよ。

(1) 関数\(y = |x-1| + |x-2|\)の表すグラフをかけ。
(2) \(x\)の方程式\(|x-1| + |x-2|-k=0\)が無数の実数解をもつときの\(k\)の値を求めよ。

解答

(1) 省略。

(2) \(k = 1\)

練習問題2-5【No.14】

問．次の各問いに答えよ。

(1) 関数\( y = |x^2-2x|+|x-1|\)の表すグラフをかけ。
(2) \(x\)の方程式\( |x^2-2x|+|x-1|-k = 0\)が異なる６つの実数解をもつときの\(k\)の値の範囲を求めよ。

解答

(1) 省略。

(2) \(\displaystyle 1 < k < \frac{5}{4} \)

練習問題の模範解答も販売中！

１分野２００円なので、解答が欲しい分野だけ格安で購入できます！！

別解や思考方法、注意点、補足説明など、note記事だからできる、他にはなかなか無い模範解答に仕上がっています。

絶対値がついた二次関数のまとめ

絶対値がついた関数のグラフのかき方についてでした。

全体に絶対値がついたり、＋定数項程度なら、グラフの折り返し。
一部（二次関数でいえば、一次の部分）に絶対値がついているケースは場合分け。

この２つの感覚をもっていれば大丈夫です。